第七章.机器学习 Scikit-Learn
7.1 Scikit-Learn简介
Scikit-Learn简称(SKlearn)是Python的第三方模块,是机器学习领域当中知名的Python模块之一,对常用的机器学习算法进行了封装,包括回归(Regression),降维(Dimensionality Reduction),分类(Classfication),聚类(Clustering)四大机器学习算法。
1.Scikit-Learn安装指令
1).pip工具安装
pip install -U scikit-learn
2).conda工具安装
conda install scikit-learn
2.线性模型
· 线性回归:利用数理统计中的回归分析,来确定两种或两种以上变量间,相互依赖的定量关系的一种统计分析与预测的方法.
· 一元线性回归分析:只包含一个自变量和一个因变量,且二者之间的关系可用一条直接近似表示。
· 多元线性回归分析:只包含两个或两个以上的自变,且自变量和因变量之间是线性关系。
· 在python中直接调用Scikit-Learn中的linear_model模块就可以实现线性回归分析,导入from sklearn import linear_model即可。
1).最小二乘法回归:(linear_model.LinearRegression)
·目的:通过最小化误差的平方和,使得预测值和真值无限接近。
·语法:
linear_model.LinearRegression(fit_intercept=True,copy_X=True, n_jobs=None)
参数说明:
fit_intercept:是否需要计算截距,布尔类型,默认值为True
copy_X:是否复制X数据,默认值为True
n_jobs:CPU的工作核数,整数,默认值为1,-1:表示和CPU核数一致。
主要属性:
coef_:数组或形状,表示线性回归分析的回归系数
intercept:数组,表示截距
主要方法:
fit(X,y,sample_weight=None):拟合线性模型
predict(X):使用线性回归模型返回预测数据
score(X,y,sample_weight=None):返回预测的确定系数R^2
·示例:
Excel中的数据:

代码:
import pandas as pd
import matplotlib as plt
from sklearn import linear_model
pd.set_option('display.unicode.east_asian_width', True)
df = pd.read_excel('F:\\Note\\清单.xlsx', sheet_name='Sheet10')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文乱码
plt.rcParams['axes.unicode_minus'] = False # 解决负号不显示的问题
area = pd.DataFrame(df['面积'])
price = pd.DataFrame(df['价格'])
# 最小二乘法回归
clf = linear_model.LinearRegression()
# 拟合线性模型
clf.fit(area, price)
# 回归系数
k = clf.coef_
print('回归系数=', k)
# 截距
b = clf.intercept_
print('截距=', b)
# 预测面积所对应的价格
area_pre = pd.DataFrame({'面积': df['预测面积']})
# 预测值
y = clf.predict(area_pre)
print('预测值=', y)
# 确定系数R^2
score = clf.score(area, price)
print('R^2=', score)
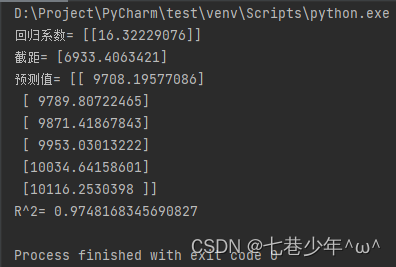
结果展示:
2).岭回归:(linear_model.Ridge)
·岭回归是在最小二乘法回归的基础上,加入了对回归系数L2范数的约束,岭回归是缩减法的一种,对回归系数的大小进行了限制。
·语法:
linear_model.Ridge( alpha=1.0,fit_intercept=True,copy_X=True, max_iter=None,tol=1e-4,solver="auto",positive=False,random_state=None)
参数说明:
alpha:权重
fit_intercept:是否需要计算截距,布尔类型,默认值为True
copy_X:是否复制X数据,默认值为True
max_iter:最大迭代次数
tol:控制求解的精度,浮点数
solver:求解器,值为:auto(默认值),svd,cholesky,sparse_cg和lsqr。
·示例:
Excel中的数据:
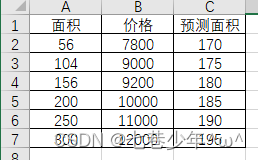
代码:
import pandas as pd
import matplotlib as plt
from sklearn import linear_model
pd.set_option('display.unicode.east_asian_width', True)
df = pd.read_excel('F:\\Note\\清单.xlsx', sheet_name='Sheet10')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文乱码
plt.rcParams['axes.unicode_minus'] = False # 解决负号不显示的问题
area = pd.DataFrame(df['面积'])
price = pd.DataFrame(df['价格'])
# 岭回归
clf = linear_model.Ridge()
# 拟合线性模型
clf.fit(area, price)
# 回归系数
k = clf.coef_
print('回归系数=', k)
# 截距
b = clf.intercept_
print('截距=', b)
# 预测面积所对应的价格
area_pre = pd.DataFrame({'面积': df['预测面积']})
# 预测值
y = clf.predict(area_pre)
print('预测值=', y)
# 确定系数R^2
score = clf.score(area, price)
print('R^2=', score)
结果展示:
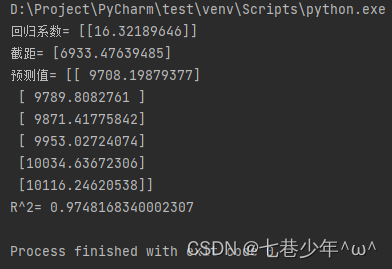
3.支持向量机(sklearn.svm.linearSVR)
支持向量机(SVMs)可用于监督学习算法,主要包括分类,回归和异常检测,支持向量分类的方法可以被扩展用作解决回归问题,这个方法被称作支持向量回归。
1).语法:
sklearn.svm.linearSVR( epsilon=0.0,tol=1e-4,C=1.0,loss="epsilon_insensitive",fit_intercept=True,intercept_scaling=1.0,dual=True,verbose=0, random_state=None,max_iter=1000)
参数说明:
epsilon:float类型,默认值为0.1
tol:终止迭代的标准值,float类型,默认值为0.0001
C:罚项参数,该参数越大,使用的正则化越少,默认值为1.0
loss:损失函数(字符串类型),参数的两个选项:epsilon_insensitive:损失函数为Lε(标准SVR),默认值;squared_epsilon_insensitive:损失函数为Lε^2
fit_intercept:是否计算此模型的截距,默认值为True
intercept_scaling:float类型,intercept_scaling=True,实例向量x变为[x,self.intercept_scaling],相当于增加了一个特征,该特征将对所有实例都显示为常数值。此时截距变成intercept_scaling特征的权重wε,此时该特征值也参与了罚项的计算
dual:选择算法是解决对偶问题还是原始问题,dual=True,解决对偶问题
verbose:是否开启verbose输出,默认值为True
random_state:int类型,随机数生成器的种子,用于在混洗数据时时使用,如果是整数:随机数生成器使用的种子,如果是RandomState示例,则是随机数生成器。
max_iter:运行的最大迭代次数,默认值为1000
coef_:特征的权重,返回array数据类型
intercept_0:决策函数中的常量,返回array数据类型。
4.K_means聚类算法
·聚类类似于分类,不同的是聚类所要求划分的类是未知的,通过算法自动分类,k_means算法是一种无监督学习算法,目的是将相似的对象归到同一簇中,簇内的对象越相似,聚类的效果就越好。
·K_means聚类是给定一个数据点集合和需要的聚类数目K,K由用户指定,K均值算法将根据某个距离函数反复把数据分入到k的聚类中。
1).聚类数据生成器的语法:
sklearn.datasets.make_blobs(n_samples=100,n_features=2,centers=None,cluster_std=1.0,center_box=(-10.0, 10.0),shuffle=True,random_state=None, return_centers=False)
参数说明:
n_samples:待生成的样本总数
n_features:每个样本的特征数
centers:类别数
cluster_std:每个类别的方差。例如:生成两类数据,其中一类比另一类具有更大的方差,可以将cluster_std参数设置为[1.0,3.0]
2).K_means聚类的语法:
KMeans( n_clusters=8,init="k-means++",n_init="warn", max_iter=300,tol=1e-4,verbose=0,random_state=None,copy_x=True,algorithm="lloyd")
参数说明:
n_clusters:生成的聚类数,及产生的质心数,默认值为8.
init:参数值为k-means++,random或者传递一个数组向量,k-means++:用一种特殊方法选定初始质心从而加速迭代过程的收敛;random:随机从训练数据中选取初始质心;传递数组向量:应该是shape(n_clusters,n_clusters)的形式,并给出初始质心
n_init:用不同的质心初始化值运行算法的系数,默认值为10
max_iter:每执行一次K_means算法的最大迭代次数,默认值为300
tol:求解的精度,默认值为1e-4
verbose:冗长的模式
random_state:用于初始化质心的生成器,整型或者随机数组类型,整型:确定一个种子(seed),默认是NumPy的随机数生成器
copy_x:是否对源数据进行复制,copy_x=True,原始数据不会发生变化,copy_x=False,则会直接在原始数据上进行修改,并在函数返回值时将其还原,但是在计算过程中,有对数据均值的加减运算,所以数据返回后,原始数据同计算前的数据可能会有细小变化。
algorithm:表示K_means算法法则,参考值:auto(默认值),full或elkan
主要属性:
cluster_centers_:聚类中心坐标值,返回数组类型
labels_:每个样本数据所属的类别标记,返回数组类型
inertia_:每个样本数据距离他们各自最近簇的中心之和,返回数组类型
主要方法:
fit(X[,y]):计算K_means聚类
fit_predict(X[,y]):计算簇质心并给每个样本数据预测类别
predict(X):给每个样本估计最近的簇
score(X[,y]):计算聚类误差
3).示例:
代码:
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成用于聚类的数据(500个样本,每个样本中含有两个特征)
x, y = make_blobs(n_samples=500, n_features=2, centers=3)
# 生成的聚类数,及产生的质心数
kmodel = KMeans(n_clusters=4, n_init='auto', random_state=9)
# 预测类别
y_pred = kmodel.fit_predict(x)
print('预测类别:', y_pred)
# 聚类中心坐标值
center_coor = kmodel.cluster_centers_
print('聚类中心坐标值', center_coor)
# 样本数据所属类别
category = kmodel.labels_
print('样本数据所属类别:', category)
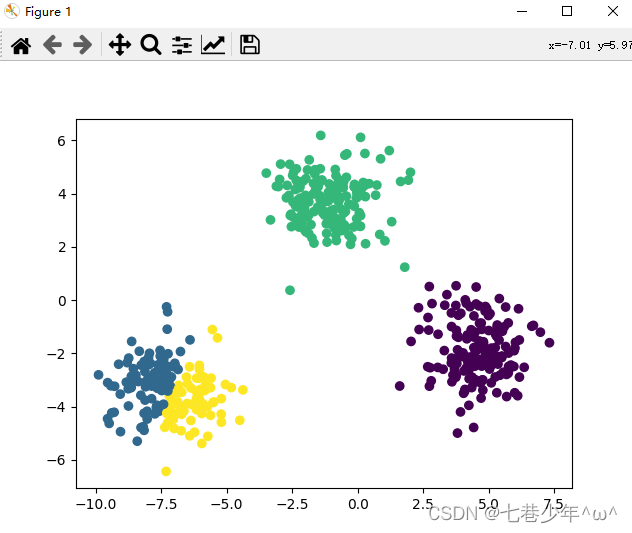
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()
结果展示: