用javascript分类刷leetcode18.队列(图文视频讲解)

队列的特点：先进先出（FIFO）
队列的时间复杂度：入队和出队O(1)，查找O(n)
优先队列：priorityQueue，按优先级出队，实现 Heap(Binary,Fibonacci...)
js里没有队列，但是可以用数组模拟

ds_29

225. 用队列实现栈 (easy)

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

1 <= x <= 9
最多调用100 次 push、pop、top 和 empty
每次调用 pop 和 top 都保证栈不为空

进阶：你能否仅用一个队列来实现栈。

方法1.使用两个 Queue 实现

思路：还是考察栈和队列的熟悉程度，没有什么具体的工程实际意义，可以用两个队列来实现栈的功能，但是一个队列的数据导入另一个队列顺序还是没有改变，所以其中一个队列只是用来做备份的，在代码里queue2就是备份队列，入栈的时候，队列1入队，出栈的时候，如果队列1为空，则交换队列1和队列2，为的是将备份队列的元素全部加入队列1，然后将队列1中除了最后一个元素外全部出队，并且加入备份队列，
复杂度分析：push的时间复杂度为O(1)，pop的时间复杂度为O(n)。空间复杂度O(n)，其中n是栈内元素的个数，用两个队列来存储

动画过大，点击查看

Js:

var MyStack = function() {
    this.queue1 = [];
    this.queue2 = [];//备份的队列
};

MyStack.prototype.push = function(x) {
    this.queue1.push(x);
};

MyStack.prototype.pop = function() {
      // 减少两个队列交换的次数， 只有当queue1为空时，交换两个队列
    if(!this.queue1.length) {
        [this.queue1, this.queue2] = [this.queue2, this.queue1];
    }
    while(this.queue1.length > 1) {//当队列1的元素数量大于1的时候不断将元素push进备份队列
        this.queue2.push(this.queue1.shift());
    }
    return this.queue1.shift();//最后将队列1最后一个元素出队
};

MyStack.prototype.top = function() {
    const x = this.pop();//查看栈顶，队列出队，然后在push进队列1
    this.queue1.push(x);
    return x;
};

MyStack.prototype.empty = function() {
    return !this.queue1.length && !this.queue2.length;
};

方法2.使用一个队列实现

动画过大，点击查看

思路：使用一个队列实现，入栈的时候直接push进队列就行，出栈的时候将除了最后一个元素外的元素全部加入到队尾。
复杂度分析：push的时间复杂度为O(1)，pop的时间复杂度为O(n)，空间复杂度O(n)

js:

var MyStack = function() {
    this.queue = [];
};

MyStack.prototype.push = function(x) {
    this.queue.push(x);
};

MyStack.prototype.pop = function() {
    let size = this.queue.length;
    while(size-- > 1) {//将除了最后一个元素外的元素全部加入到队尾。
        this.queue.push(this.queue.shift());
    }
    return this.queue.shift();
};

MyStack.prototype.top = function() {
    const x = this.pop();//先出栈，然后在加入队列
    this.queue.push(x);
    return x;
};

MyStack.prototype.empty = function() {
    return !this.queue.length;
};

933. 最近的请求次数 (easy)

写一个 RecentCounter 类来计算特定时间范围内最近的请求。

请你实现 RecentCounter 类：

RecentCounter() 初始化计数器，请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求，其中 t 表示以毫秒为单位的某个时间，并返回过去 3000 毫秒内发生的所有请求数（包括新请求）。确切地说，返回在 [t-3000, t] 内发生的请求数。
保证每次对 ping 的调用都使用比之前更大的 t 值。

示例 1：

输入：
[“RecentCounter”, “ping”, “ping”, “ping”, “ping”]
[[], [1], [100], [3001], [3002]]
输出：
[null, 1, 2, 3, 3]

解释：
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = [1]，范围是 [-2999,1]，返回 1
recentCounter.ping(100); // requests = [1, 100]，范围是 [-2900,100]，返回 2
recentCounter.ping(3001); // requests = [1, 100, 3001]，范围是 [1,3001]，返回 3
recentCounter.ping(3002); // requests = [1, 100, 3001, 3002]，范围是 [2,3002]，返回 3

提示：

1 <= t <= 109
保证每次对 ping 调用所使用的 t 值都严格递增
至多调用 ping 方法 104 次

思路：将请求加入队列，如果队头元素请求的时间在[t-3000,t]之外就不断出队
复杂度：时间复杂度O(q)，q是ping的次数。空间复杂度O(w)，w是队列中最多的元素个数

js：

var RecentCounter = function() {
    this.queue = []
};

RecentCounter.prototype.ping = function(t) {
    this.queue.push(t);//新请求入队
    const time = t-3000;//计算3000ms前的时间
    while(this.queue[0] < time){//如果队头元素请求的时间在[t-3000,t]之外 就不断出队
        this.queue.shift();
    }
    return this.queue.length;//在[t-3000,t]区间内队列剩余的元素就是符合要求的请求数
};

703. 数据流中的第 K 大元素 (easy)

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。
int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

示例：

输入：
[“KthLargest”, “add”, “add”, “add”, “add”, “add”]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
输出：
[null, 4, 5, 5, 8, 8]

解释：
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8

提示：
1 <= k <= 104
0 <= nums.length <= 104
-104 <= nums[i] <= 104
-104 <= val <= 104
最多调用 add 方法 104 次
题目数据保证，在查找第 k 大元素时，数组中至少有 k 个元素

方法1:暴力排序

思路：当数据流有新的元素的时候，重新按升序排序数组，倒数第k个元素就是第k大的数
复杂度分析：时间复杂度O(c*zlogz)，z为数据流的最长长度，c为加入元素的个数，排序复杂度是O(zlogz)，加入c次排序就需要排序c次。

方法2:堆

ds_32

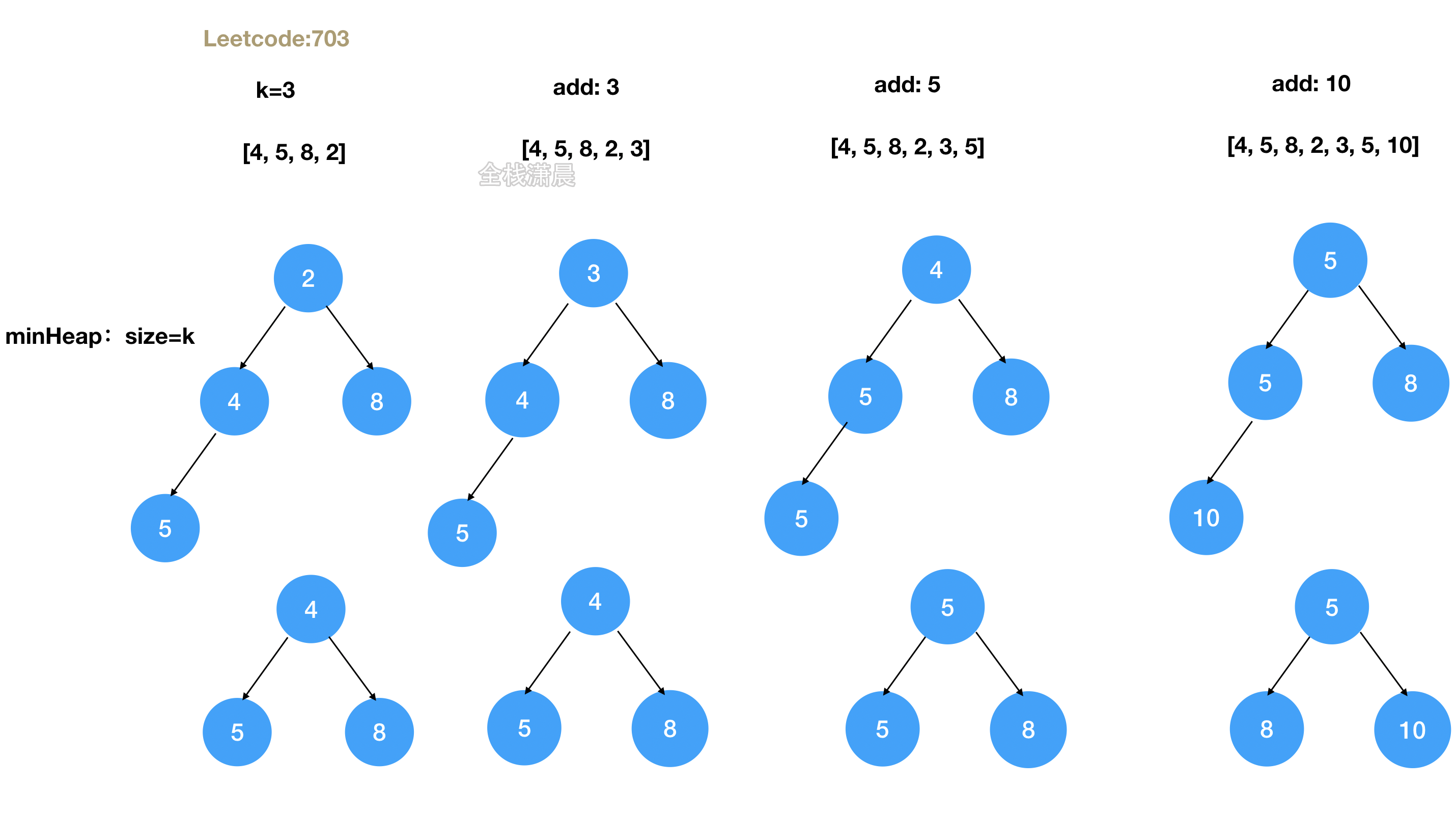
思路：用一个size是k的小顶堆来存贮前k个元素，堆顶是最小的元素，在循环数组的过程中，不断加入元素然后调整元素在堆中的位置，如果此时优先队列的大小大于 k，我们需要将优先队列的队头元素弹出，以保证优先队列的大小为 k，最后堆顶就是第K大元素的位置
复杂度分析：时间复杂度O(nlogk)，n是初始数组的大小，k是堆的大小，初始堆化和单次插入堆的复杂度都是O(logk)，数组的每个数都要插入堆中一次，所以是O(nlogk)。空间复杂度：O(k), 即堆的大小

js:

var KthLargest = function (k, nums) {
    this.k = k;
    this.heap = new Heap();
    for (const x of nums) {//将数组中的数加入小顶堆
        this.add(x);//加入小顶堆
    }
};

KthLargest.prototype.add = function (val) {
    this.heap.offer(val);//加入堆
    if (this.heap.size() > this.k) {//大小超过了小顶堆的size，就从小顶堆删除一个最小的元素
        this.heap.poll();//删除最小的元素
    }
    return this.heap.peek();//返回堆顶
};

class Heap {
    constructor(comparator = (a, b) => a - b, data = []) {
        this.data = data;
        this.comparator = comparator;//比较器
        this.heapify();//堆化
    }

    heapify() {
        if (this.size() < 2) return;
        for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
            this.bubbleDown(i);//bubbleDown操作
        }
    }

    peek() {
        if (this.size() === 0) return null;
        return this.data[0];//查看堆顶
    }

    offer(value) {
        this.data.push(value);//加入数组
        this.bubbleUp(this.size() - 1);//调整加入的元素在小顶堆中的位置
    }

    poll() {
        if (this.size() === 0) {
            return null;
        }
        const result = this.data[0];
        const last = this.data.pop();
        if (this.size() !== 0) {
            this.data[0] = last;//交换第一个元素和最后一个元素
            this.bubbleDown(0);//bubbleDown操作
        }
        return result;
    }

    bubbleUp(index) {
        while (index > 0) {
            const parentIndex = (index - 1) >> 1;//父节点的位置
            //如果当前元素比父节点的元素小，就交换当前节点和父节点的位置
            if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
                this.swap(index, parentIndex);//交换自己和父节点的位置
                index = parentIndex;//不断向上取父节点进行比较
            } else {
                break;//如果当前元素比父节点的元素大，不需要处理
            }
        }
    }

    bubbleDown(index) {
        const lastIndex = this.size() - 1;//最后一个节点的位置
        while (true) {
            const leftIndex = index * 2 + 1;//左节点的位置
            const rightIndex = index * 2 + 2;//右节点的位置
            let findIndex = index;//bubbleDown节点的位置
            //找出左右节点中value小的节点
            if (
                leftIndex <= lastIndex &&
                this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
            ) {
                findIndex = leftIndex;
            }
            if (
                rightIndex <= lastIndex &&
                this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
            ) {
                findIndex = rightIndex;
            }
            if (index !== findIndex) {
                this.swap(index, findIndex);//交换当前元素和左右节点中value小的
                index = findIndex;
            } else {
                break;
            }
        }
    }

    swap(index1, index2) {//交换堆中两个元素的位置
        [this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
    }

    size() {
        return this.data.length;
    }
}

347. 前 K 个高频元素（medium）

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按任意顺序返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:

输入: nums = [1], k = 1
输出: [1]

提示：

1 <= nums.length <= 105
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

进阶：你所设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小。

方法1:优先队列

ds_127

思路：循环数组，加入小顶堆，当堆的size超过k时，出堆，循环完成之后，堆中所有的元素就是前k大的数字
复杂度：时间复杂度O(nlogk)，循环n次，每次堆的操作是O(logk)。空间复杂度O(k)，

js：

class Heap {
    constructor(comparator = (a, b) => a - b, data = []) {
        this.data = data;
        this.comparator = comparator;//比较器
        this.heapify();//堆化
    }

    heapify() {
        if (this.size() < 2) return;
        for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
            this.bubbleDown(i);//bubbleDown操作
        }
    }

    peek() {
        if (this.size() === 0) return null;
        return this.data[0];//查看堆顶
    }

    offer(value) {
        this.data.push(value);//加入数组
        this.bubbleUp(this.size() - 1);//调整加入的元素在小顶堆中的位置
    }

    poll() {
        if (this.size() === 0) {
            return null;
        }
        const result = this.data[0];
        const last = this.data.pop();
        if (this.size() !== 0) {
            this.data[0] = last;//交换第一个元素和最后一个元素
            this.bubbleDown(0);//bubbleDown操作
        }
        return result;
    }

    bubbleUp(index) {
        while (index > 0) {
            const parentIndex = (index - 1) >> 1;//父节点的位置
            //如果当前元素比父节点的元素小，就交换当前节点和父节点的位置
            if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
                this.swap(index, parentIndex);//交换自己和父节点的位置
                index = parentIndex;//不断向上取父节点进行比较
            } else {
                break;//如果当前元素比父节点的元素大，不需要处理
            }
        }
    }

    bubbleDown(index) {
        const lastIndex = this.size() - 1;//最后一个节点的位置
        while (true) {
            const leftIndex = index * 2 + 1;//左节点的位置
            const rightIndex = index * 2 + 2;//右节点的位置
            let findIndex = index;//bubbleDown节点的位置
            //找出左右节点中value小的节点
            if (
                leftIndex <= lastIndex &&
                this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
            ) {
                findIndex = leftIndex;
            }
            if (
                rightIndex <= lastIndex &&
                this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
            ) {
                findIndex = rightIndex;
            }
            if (index !== findIndex) {
                this.swap(index, findIndex);//交换当前元素和左右节点中value小的
                index = findIndex;
            } else {
                break;
            }
        }
    }

    swap(index1, index2) {//交换堆中两个元素的位置
        [this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
    }

    size() {
        return this.data.length;
    }
}

var topKFrequent = function (nums, k) {
    const map = new Map();

    for (const num of nums) {//统计频次
        map.set(num, (map.get(num) || 0) + 1);
    }

    //创建小顶堆
    const priorityQueue = new Heap((a, b) => a[1] - b[1]);

    //entry 是一个长度为2的数组，0位置存储key，1位置存储value
    for (const entry of map.entries()) {
        priorityQueue.offer(entry);//加入堆
        if (priorityQueue.size() > k) {//堆的size超过k时，出堆
            priorityQueue.poll();
        }
    }

    const ret = [];

    for (let i = priorityQueue.size() - 1; i >= 0; i--) {//取出前k大的数
        ret[i] = priorityQueue.poll()[0];
    }

    return ret;
};

23. 合并K个升序链表 (hard)

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2：

输入：lists = []
输出：[]
示例 3：

输入：lists = [[]]
输出：[]

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按升序排列
lists[i].length 的总和不超过 10^4

方法1.分治

ds_33

思路：自底而上归并，第一次归并2个链表，第二次归并4个链表…，每次归并不断合并两个有序链表，直到合并完所有分治后的链表
复杂度：时间复杂度O(n * logk)，n是每个链表节点数，k个链表个数，每次归并，链表数量较少一半，复杂度是O(logk)，将两个链表合并成一个顺序链表复杂度是O(2n)，所以时间复杂度是 O(n * logk)。空间复杂度是O(logk)，即递归的空格复杂度

js:

//自顶而下归并 先分在合
var mergeKLists = function (lists) {
    // 当是空数组的情况下
    if (!lists.length) {
        return null;
    }
    // 合并两个排序链表
    const merge = (head1, head2) => {
        let dummy = new ListNode(0);
        let cur = dummy;
        // 新链表，新的值小就先接谁
        while (head1 && head2) {
            if (head1.val < head2.val) {
                cur.next = head1;
                head1 = head1.next;
            } else {
                cur.next = head2;
                head2 = head2.next;
            }
            cur = cur.next;
        }
        // 如果后面还有剩余的就把剩余的接上
        cur.next = head1 == null ? head2 : head1;
        return dummy.next;
    };
    const mergeLists = (lists, start, end) => {
        if (start + 1 == end) {
            return lists[start];
        }
        // 输入的k个排序链表，可以分成两部分，前k/2个链表和后k/2个链表
        // 如果将这前k/2个链表和后k/2个链表分别合并成两个排序的链表，再将两个排序的链表合并，那么所有链表都合并了
        let mid = (start + end) >> 1;
        let head1 = mergeLists(lists, start, mid);
        let head2 = mergeLists(lists, mid, end);
        return merge(head1, head2);
    };
    return mergeLists(lists, 0, lists.length);
};

//自底而上合并
var mergeKLists = function (lists) {
    if (lists.length <= 1) return lists[0] || null;//当归并的节点只有一个时 返回这个节点
    const newLists = [];
    //自底而上归并，第一次归并大小为2的链表，第二次归并大小4的链表...
    for (let i = 0; i < lists.length; i += 2) {
        newLists.push(merge(lists[i], lists[i + 1] || null));
    }
    return mergeKLists(newLists);
};

const merge = (list_1, list_2) => {//合并两个有序链表
    const dummyNode = new ListNode(0);
    let p = dummyNode;

    while (list_1 && list_2) {
        if (list_1.val < list_2.val) {//先将小的节点加入
            p.next = list_1;
            list_1 = list_1.next;
        } else {
            p.next = list_2;
            list_2 = list_2.next;
        }
        p = p.next;
    }

    p.next = list_1 ? list_1 : list_2;//遍历完成还有节点剩余
    return dummyNode.next;
};

方法2.优先队列

ds_34

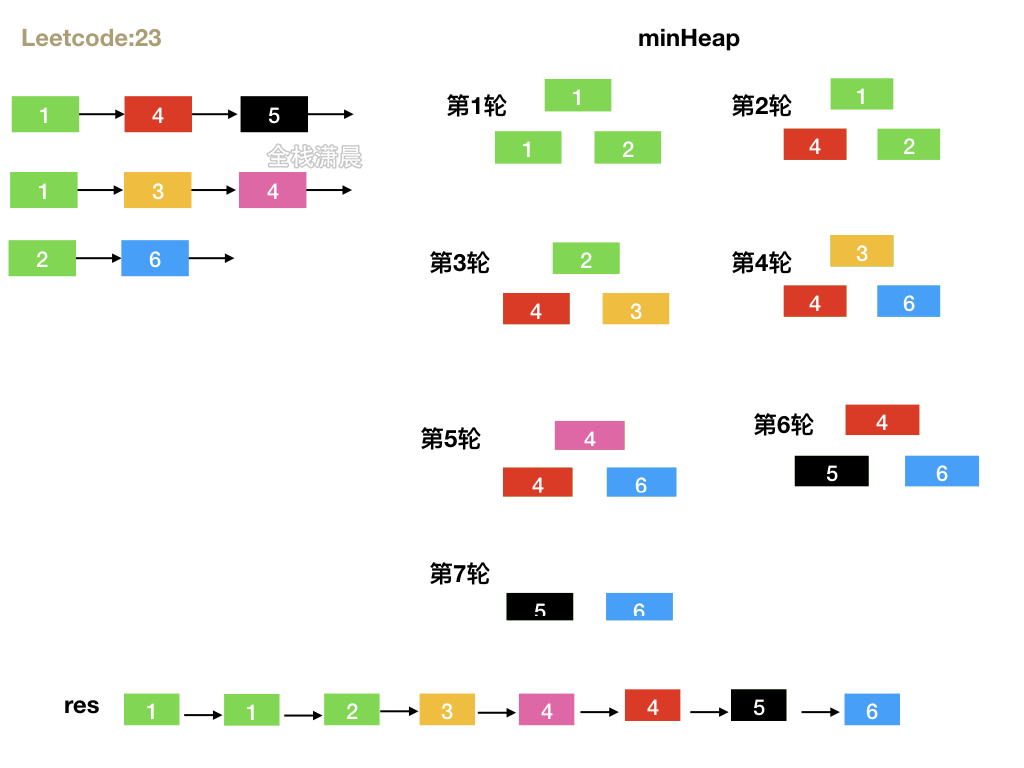
思路：新建小顶堆，小顶堆的大小是k，不断从每个链表的头节点开始不断加入小顶堆中，然后取出堆顶值，也就是最小值，然后继续往小顶堆中插入这个最小值在链表的next节点
复杂度：时间复杂度O(kn * logk)，优先队列的大小是k，每次插入和删除是O(logk)，总共k * n的节点个数，每个节点插入删除一次，所以总的复杂度是O(kn*logk)。空间复杂度是O(k)，即优先队列的大小

js:

class Heap {
    constructor(comparator = (a, b) => a - b, data = []) {
        this.data = data;
        this.comparator = comparator;//比较器
        this.heapify();//堆化
    }

    heapify() {
        if (this.size() < 2) return;
        for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
            this.bubbleDown(i);//bubbleDown操作
        }
    }

    peek() {
        if (this.size() === 0) return null;
        return this.data[0];//查看堆顶
    }

    offer(value) {
        this.data.push(value);//加入数组
        this.bubbleUp(this.size() - 1);//调整加入的元素在小顶堆中的位置
    }

    poll() {
        if (this.size() === 0) {
            return null;
        }
        const result = this.data[0];
        const last = this.data.pop();
        if (this.size() !== 0) {
            this.data[0] = last;//交换第一个元素和最后一个元素
            this.bubbleDown(0);//bubbleDown操作
        }
        return result;
    }

    bubbleUp(index) {
        while (index > 0) {
            const parentIndex = (index - 1) >> 1;//父节点的位置
            //如果当前元素比父节点的元素小，就交换当前节点和父节点的位置
            if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
                this.swap(index, parentIndex);//交换自己和父节点的位置
                index = parentIndex;//不断向上取父节点进行比较
            } else {
                break;//如果当前元素比父节点的元素大，不需要处理
            }
        }
    }

    bubbleDown(index) {
        const lastIndex = this.size() - 1;//最后一个节点的位置
        while (true) {
            const leftIndex = index * 2 + 1;//左节点的位置
            const rightIndex = index * 2 + 2;//右节点的位置
            let findIndex = index;//bubbleDown节点的位置
            //找出左右节点中value小的节点
            if (
                leftIndex <= lastIndex &&
                this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
            ) {
                findIndex = leftIndex;
            }
            if (
                rightIndex <= lastIndex &&
                this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
            ) {
                findIndex = rightIndex;
            }
            if (index !== findIndex) {
                this.swap(index, findIndex);//交换当前元素和左右节点中value小的
                index = findIndex;
            } else {
                break;
            }
        }
    }

    swap(index1, index2) {//交换堆中两个元素的位置
        [this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
    }

    size() {
        return this.data.length;
    }
}

var mergeKLists = function(lists) {
    const res = new ListNode(0);
    let p = res;
    const h = new Heap(comparator = (a, b) => a.val - b.val);
    lists.forEach(l => {//插入每个链表的第一个节点
        if(l) h.offer(l);
    })
    while(h.size()) {//
        const n = h.poll();//取出最小值
        p.next = n;//最小值加入p的next后
        p = p.next;//移动p节点
        if(n.next) h.offer(n.next);//插入最小节点的后一个节点
    }
    return res.next;
};

692. 前K个高频单词(medium)

给定一个单词列表 words 和一个整数 k ，返回前 k 个出现次数最多的单词。

返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率，按字典顺序排序。

示例 1：

输入: words = [“i”, “love”, “leetcode”, “i”, “love”, “coding”], k = 2
输出: [“i”, “love”]
解析: “i” 和 “love” 为出现次数最多的两个单词，均为2次。
注意，按字母顺序 “i” 在 “love” 之前。
示例 2：

输入: [“the”, “day”, “is”, “sunny”, “the”, “the”, “the”, “sunny”, “is”, “is”], k = 4
输出: [“the”, “is”, “sunny”, “day”]
解析: “the”, “is”, “sunny” 和 “day” 是出现次数最多的四个单词，
出现次数依次为 4, 3, 2 和 1 次。

注意：

1 <= words.length <= 500
1 <= words[i] <= 10
words[i] 由小写英文字母组成。
k 的取值范围是 [1, 不同 words[i] 的数量]

方法1:排序

js：

var topKFrequent = function (words, k) {
    const map = {};
    words.forEach(v => map[v] = (map[v] || 0) + 1);
    const keys = Object.keys(map).sort((a, b) => map[b] - map[a] || a.localeCompare(b))
    return keys.slice(0, k);
};

方法2：堆

js:

class Heap {
    constructor(comparator = (a, b) => a - b, data = []) {
        this.data = data;
        this.comparator = comparator;//比较器
        this.heapify();//堆化
    }

    heapify() {
        if (this.size() < 2) return;
        for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
            this.bubbleDown(i);//bubbleDown操作
        }
    }

    peek() {
        if (this.size() === 0) return null;
        return this.data[0];//查看堆顶
    }

    offer(value) {
        this.data.push(value);//加入数组
        this.bubbleUp(this.size() - 1);//调整加入的元素在小顶堆中的位置
    }

    poll() {
        if (this.size() === 0) {
            return null;
        }
        const result = this.data[0];
        const last = this.data.pop();
        if (this.size() !== 0) {
            this.data[0] = last;//交换第一个元素和最后一个元素
            this.bubbleDown(0);//bubbleDown操作
        }
        return result;
    }

    bubbleUp(index) {
        while (index > 0) {
            const parentIndex = (index - 1) >> 1;//父节点的位置
            //如果当前元素比父节点的元素小，就交换当前节点和父节点的位置
            if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
                this.swap(index, parentIndex);//交换自己和父节点的位置
                index = parentIndex;//不断向上取父节点进行比较
            } else {
                break;//如果当前元素比父节点的元素大，不需要处理
            }
        }
    }

    bubbleDown(index) {
        const lastIndex = this.size() - 1;//最后一个节点的位置
        while (true) {
            const leftIndex = index * 2 + 1;//左节点的位置
            const rightIndex = index * 2 + 2;//右节点的位置
            let findIndex = index;//bubbleDown节点的位置
            //找出左右节点中value小的节点
            if (
                leftIndex <= lastIndex &&
                this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
            ) {
                findIndex = leftIndex;
            }
            if (
                rightIndex <= lastIndex &&
                this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
            ) {
                findIndex = rightIndex;
            }
            if (index !== findIndex) {
                this.swap(index, findIndex);//交换当前元素和左右节点中value小的
                index = findIndex;
            } else {
                break;
            }
        }
    }

    swap(index1, index2) {//交换堆中两个元素的位置
        [this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
    }

    size() {
        return this.data.length;
    }
}

var topKFrequent = function (nums, k) {
    const map = new Map();

    for (const num of nums) {//统计频次
        map.set(num, (map.get(num) || 0) + 1);
    }

    //创建小顶堆
    const priorityQueue = new Heap((a, b) => {
        return a[1] === b[1] ? b[0].localeCompare(a[0]) : a[1] - b[1]
    });

    //entry 是一个长度为2的数组，0位置存储key，1位置存储value
    for (const entry of map.entries()) {
        priorityQueue.offer(entry);//加入堆
        if (priorityQueue.size() > k) {//堆的size超过k时，出堆
            priorityQueue.poll();
        }
    }

    const ret = [];

    for (let i = priorityQueue.size() - 1; i >= 0; i--) {//取出前k大的数
        ret[i] = priorityQueue.poll()[0];
    }

    return ret;
};

622. 设计循环队列 (medium)

设计你的循环队列实现。循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1); // 返回 true
circularQueue.enQueue(2); // 返回 true
circularQueue.enQueue(3); // 返回 true
circularQueue.enQueue(4); // 返回 false，队列已满
circularQueue.Rear(); // 返回 3
circularQueue.isFull(); // 返回 true
circularQueue.deQueue(); // 返回 true
circularQueue.enQueue(4); // 返回 true
circularQueue.Rear(); // 返回 4

提示：

所有的值都在 0 至 1000 的范围内；
操作数将在 1 至 1000 的范围内；
请不要使用内置的队列库。

复杂度:时间复杂度O(1)，空间复杂度O(k)

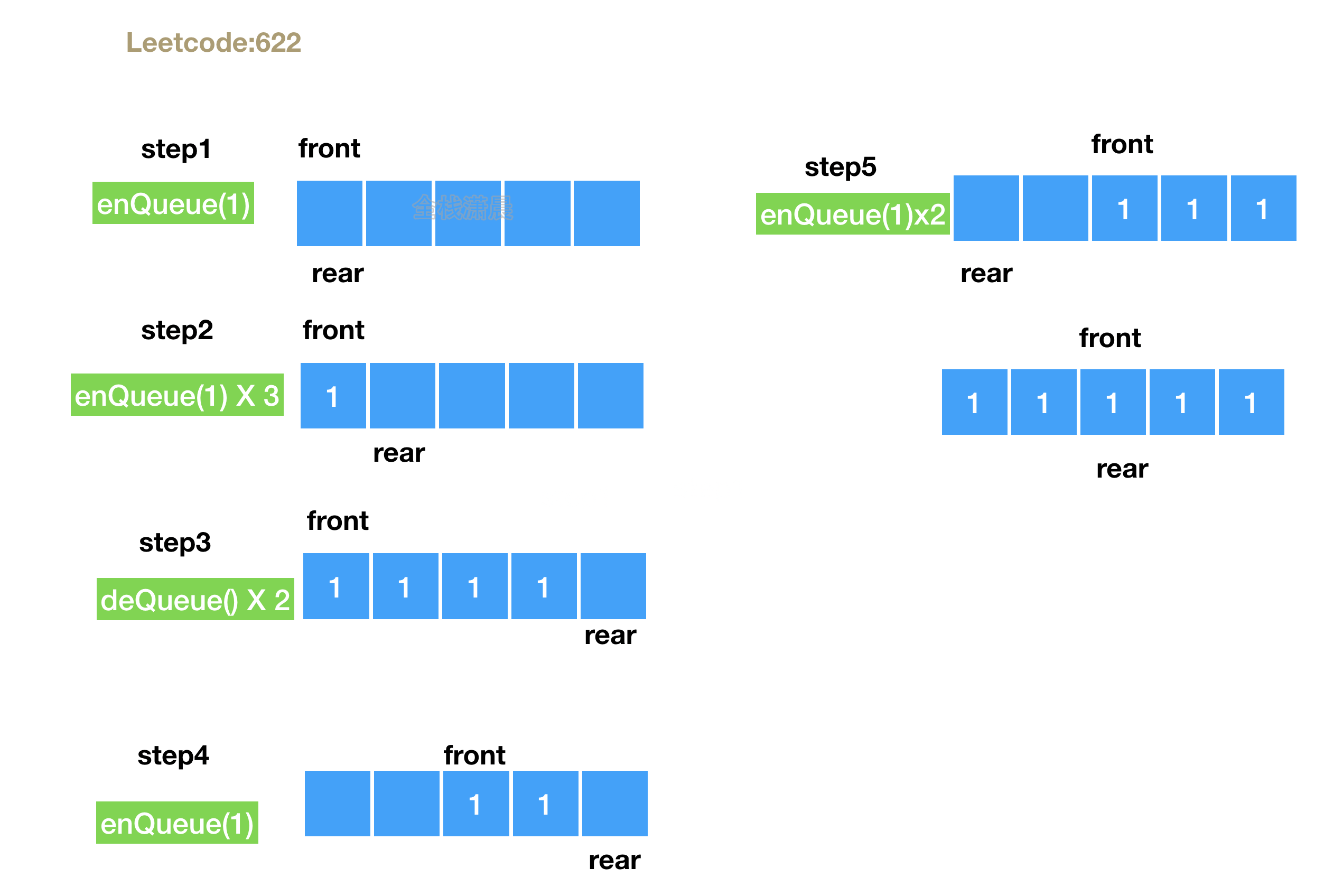
js:

var MyCircularQueue = function(k) {
    this.front = 0
    this.rear = 0
    this.max = k
    this.list = Array(k)
};

MyCircularQueue.prototype.enQueue = function(value) {
    if(this.isFull()) {
        return false
    } else {
        this.list[this.rear] = value
        this.rear = (this.rear + 1) % this.max
        return true
    }
};

MyCircularQueue.prototype.deQueue = function() {
    let v = this.list[this.front]
    this.list[this.front] = undefined
    if(v !== undefined ) {
        this.front = (this.front + 1) % this.max
        return true
    } else {
        return false
    }
};

MyCircularQueue.prototype.Front = function() {
    if(this.list[this.front] === undefined) {
        return -1
    } else {
        return this.list[this.front]
    }
};

MyCircularQueue.prototype.Rear = function() {
    let rear = this.rear - 1
    if(this.list[rear < 0 ? this.max - 1 : rear] === undefined) {
        return -1
    } else {
        return this.list[rear < 0 ? this.max - 1 : rear] 
    }
};

MyCircularQueue.prototype.isEmpty = function() {
    return this.front === this.rear && !this.list[this.front]
};

MyCircularQueue.prototype.isFull = function() {
    return (this.front === this.rear) && !!this.list[this.front]
};