今日复习内容:做点真题和继续复习动态规划
例题1:三国游戏
(用的知识点是贪心和排序)
题目描述:
小蓝正在玩一款游戏,游戏中魏(X),蜀(Y),吴(Z)三个国家各自拥有一定数量的士兵X,Y,Z,一开始可以认为都是0。游戏有n个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第i个事件发生时,会分别让X,Y,Z增加Ai,Bi,Ci。
当游戏结束时(所有事件的发生与否已经确定),如果X,Y,Z其中一个大于另外两个之和,我们认为其获胜。例如:X > Y + Z,我们认为魏国获胜。小蓝想知道游戏结束时如果有其中一个国家获胜,最多发生了多少个事件?如果不存在能让某国获胜的情况,请输出-1。
输入描述:
输入的第一行包含一个整数n;
第二行包含n个整数表示Ai,相邻整数之间使用一个空格分隔;
第三行包含n个整数表示Bi,相邻整数之间使用一个空格分隔;
第四行包含n个整数表示Ci,相邻整数之间使用一个空格分隔;
输出格式:
输出一行包含一个整数表示答案。
参考答案:
n = int(input())
a = list(map(int,input().split()))
b = list(map(int,input().split()))
c = list(map(int,input().split()))
def getans(a,b,c):
#ai - bi - ci
d = [a[i] - b[i] - c[i] for i in range(n)]
d1 = [d[i] for i in range(n) if d[i] > 0]
d2 = [-d[i] for i in range(n) if d[i] <= 0]
ans = len(d1)
#sum(a) - sum(b + c)
total = sum(d1)
d2.sort()
for x in d2:
if total - x > 0:
total -= x
ans += 1
else:
break
return ans一.最长上升子序列
当谈论最长上升子序列时,通常涉及以下内容:
1.定义
最长上升子序列是指在一个给定的序列中,仅需要保持元素的相对顺序不变,找到一个最长的子序列,使得子序列中的元素按照严格递增的顺序排列。
2.动态规划解法
动态规划是解决最长上升子序列问题的一种常用方法。该方法的基本思想是利用一个数组来存储以当前元素为结尾的最长上升子序列的长度。通过不断更新这个数组,最终找到整个序列的最长上升子序列长度。
3.贪心算法解法
最长上升子序列问题也可以使用贪心算法解决。贪心算法通常从局部最优解出发,逐步扩展到全局最优解。
在这个问题中,贪心算法的核心思想是尽可能地选择小的,符合递增顺序的数,以确保子序列的长度尽可能的长。
4.二分查找优化
在动态规划解法的基础上,可以通过来使用二分查找来优化算法的时间复杂度。具体做法是维护一个递增的数组,遍历序列中的每个元素,在数组中寻找第一个大于等于当前元素的位置,并更新该位置的元素为当前元素。这样可以保证数组的长度即为最长上升子序列的长度,并且数组中的元素是递增的。
5.应用
最长上升子序列问题在很大领域都有广泛的应用,比如信用卡账单问题,基因序列匹配等。解决这个问题不仅可以帮助理解动态规划和贪心算法的思想,还能够应用到实际的算法设计和优化中。
接下来做几个题:
例题2:蓝桥勇士
题目描述:
小明是蓝桥王国的勇士,他晋升为蓝桥骑士,于是他决定不断突破自我。
这天蓝桥首席骑士长给他安排了N个对手,他们的战力值分别为a1,a2,...,an,且按顺序阻挡在小明的前方,对于这些对手小明可以选择挑战,也可以选择避战。
作为热血豪放的勇士,小明从不走回头路,且只愿意挑战战力值越来越高的对手。
请你算算小明最多会挑战多少名对手?
输入描述:
输入第一行包含一个整数N,表示对手的个数;
第二行包含N个整数a1,a2,a3,...,an,分别表示对手的战力值。
1 <= N <= 10^3,1 <= ai <= 10^9。
输出描述:
输出一行整数表示答案。
参考答案:
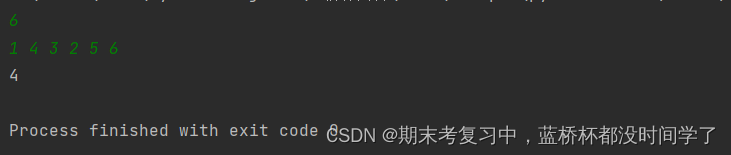
n = int(input())
a = [0] + list(map(int,input().split()))
dp = [0] + [1] * (n)
for i in range(1,n + 1):
for j in range(1,i):
if a[j] < a[i]:
dp[i] = max(dp[i],dp[j] + 1)
print(max(dp))运行结果:
例题3:合唱队形
题目描述:
N为同学站成一排,音乐老师要请其中的(N - K)位同学出列,使得剩下的K位同学拍成合唱队形。
合唱队形是指这样的一种队形:设K位同学从左到右依次编号位1,2,...,K,他们的身高分别位T1,T2,...,Tk,则他们的身高满足:T1<...<Ti > Ti+1 >...>Tk(1 <= i <= K)。
你的任务是:已知所有n位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入描述:
输入两行
第一行一个整数N(2 <= N <= 100),表示同学的总数。
第二行有N个整数,用空格分隔,第i个整数Ti(130 <= Ti <= 230)是第i位同学的身高(厘米)。
输出描述:
输出一行,包含一个整数表示答案。
参考答案:
n = int(input())
a = [0] + list(map(int,input().split()))
dp1 = [0] + [1] * (n)
for i in range(1,n + 1):
for j in range(1,i):
if a[j] < a[i]:
dp1[i] = max(dp1[i],dp1[j] + 1)
dp2 = [0] + [1] * (n)
for i in range(n,0,-1):
for j in range(i + 1,n + 1):
if a[i] > a[j]:
dp2[i] = max(dp2[i],dp2[j] + 1)
ans = max([dp1[i] + dp2[i] - 1 for i in range(n + 1)])
print(n - ans)二.最长公共子序列
当谈到最长公共子序列时,通常涉及以下知识点:
1.定义
最长公共子序列是指在两个序列中都存在的一个最长的子序列,可以不连续,但是其元素在两个序列中的相对顺序保持不变。
2.动态规划解法
动态规划是解决最长公共子序列为题的一种常见方法。该方法的基本思想是利用一个二维数组来存储两个序列之间的公共子序列的长度。
具体而言,通过迭代填充二维数组,可以得到两个序列之间每个位置处的最长公共子序列的长度,最终,右下角的元素即为两个序列的最长公共子序列的长度。
3.回溯构造最长公共子序列
在动态规划求解得到最长公共子序列的长度后,可以通过回溯的方式构造出具体的最长公共子序列。
从右下角开始,向左上方遍历二维数组,如果当前元素对应的字符相等,则将该字符添加到最长公共子序列中,并继续向左上方移动;如果不相等,则根据状态转移方程移动到上方或左方的元素。
4.应用
最长公共子序列问题应用广泛。
例题4:最长公共子序列
题目描述:
给定一个长度为N的数组a和一个长度为M的数组b。
请你求出它们的最长公共子序列的长度。
输入描述:
输入第一行包含两个整数N和M,表示数组a和数组b的长度。
第二行包含N个整数a1,a2,...,an;
第三含包含M个整数b1,b2,...,bm。
1 <= N,M <= 10^3,1 <= ai,bi <= 10^9。
输出描述:
输出一行整数表示答案。
参考答案:
n,m = map(int,input().split())
a = [0] + list(map(int,input().split()))
b = [0] + list(map(int,input().split()))
dp = [[0] * (m + 1) for i in range(n + 1)]
for i in range(1,n + 1):
for j in range(1,m + 1):
if a[i] == b[j]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j],dp[i][j - 1])
print(dp[n][m])
# 输出最长公共子序列
ans = []
x,y = n,m
while x != 0 and y != 0:
if dp[x][y] == dp[x - 1][y]:
x = x - 1
elif dp[x][y] == dp[x][y - 1]:
y = y - 1
else:
ans.append(a[x])
x,y = x - 1,y - 1
print(ans[::-1])这个题的后半段是我自己加的,只是为了验证一下答案,可以不写的(就是“#输出最长公共子序列”后面那些代码)
三.背包问题
1.问题描述
背包问题描述为:给定一个背包容量(通常为一个正整数),一组物品,每个物品都有自己的重量和价值。要求在不超过背包容量的条件下,选择一些物品放入背包,使得放入背包的物品总价值最大。
2.背包问题分类
背包问题可以分为0-1背包问题,完全背包问题和多重背包问题等不同类别,具体的区别在于对物品放入背包的限制不同。
0-1背包问题要求每个物品只能选择放入或不放入背包,不能部分放入;
完全背包问题允许每个物品可以放入多次,即可以选择放入0个,1个,2个,但不能超过背包容量。
多重背包问题允许每个物品有限制的放入次数,即每个物品有一个数量限制。
3.动态规划解法
动态规划是解决背包问题的常用方法。其基本思想是将问题划分为若干子问题,并利用子问题的解构造出原问题的解。
对应0-1背包问题,通常使用二维数组来表示状态,其中dp[i][j]表示在请i个物品中选择,在背包容量为j时能够获得的最大价值。状态转移方程通常为
dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - weight[i] + value[i]),其中weight[i]表示第i个物品的重量,value[i]表示第i个物品的价值。
对于完全背包问题和多重背包问题,状态转移方程与0-1背包问题有所不同,需要根据具体的限制条件进行调整。
例题5:小明的背包1
题目描述:
小明有一个容量为V的背包。
这天他去商场购物,商场一共有N件物品,第i件物品的体积为wi,价值为vi。
小明想知道在购买的物品总体积不超过V的情况下所能获得的最大价值是多少,请你帮他算算。
输入描述:
输入第一行包含两个整数N和V,表示商场物品的数量和小明的背包容量。
第2至n+1行包含2个正整数w,v,表示物品的体积和价值。
1 <= N <= 10^2,1 <= V <= 10^3,1 <= wi,vi <= 10^3。
输出描述:
输出一行整数表示小明所能获得的最大价值。
参考答案:
N,V = map(int,input().split())
dp = [[0] * (V + 1) for i in range(N + 1)]
for i in range(1,N + 1):
w,v = map(int,input().split())
for j in range(V + 1):
if j < w:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - w] + v)
print(dp[N][V])运行结果:


例题6:背包与魔法
题目描述:
小蓝面前有N件物品,其中第i件物品重量为Wi,价值为Vi。她还有一个背包,最大承重是M。
小蓝想知道在背包承重范围内,她总共能装总价值多少的物品?
特别值得一提的是,小蓝可以使用一个魔法(总共使用一次),将一件物品的重量增加K,同时价值翻倍,当然,小蓝也可以不使用魔法。
输入格式:
第一行包含3个整数N,M,K;
以下N行,每行两个整数Wi,Vi。
输出格式:
输出一个整数表示答案。
参考答案:
N,M,K = map(int,input().split())
dp = [[[0] * 2 for j in range(M + 1)] for i in range(N + 1)]
for i in range(1,N + 1):
w,v = map(int,input().split())
for j in range(1,M + 1):
for k in range(2):
if j < w:
dp[i][j][k] = dp[i - 1][j][k]
else:
dp[i][j][k] = max(dp[i - 1][j][k],dp[i - 1][j - w][k] + v)
if k == 1 and j <= w:
dp[i][j][k] = max(dp[i - 1][j][k],dp[i - 1][j - w - k][0] + 2 * v)
print(max(dp[N][M][1],dp[N][M][0]))我还可以给它优化一下:
N,M,K = map(int,input().split())
dp = [[[0] * 2 for j in range(M + 1)] for i in range(N + 1)]
for i in range(1,N + 1):
w,v = map(int,input().split())
for j in range(M,w - 1,-1):
dp[j][0] = max(dp[j][0],dp[j - w][0] + v)
dp[j][1] = max(dp[j][1],dp[j - w - K][0] + 2 * v)
if j >= w + K:
dp[j][1] = max(dp[j][1],dp[j - w - K][0] + 2 * v)
print(max(dp[M][1],dp[M][0]))这个题的第一个代码有一点问题,但我没有改,有需要的朋友可以来问我的。
OK,这篇就写到这里,最近我复习的状态越来越好了,下一篇继续 !