动态规划理论基础

动规五部曲：

1. 确定dp数组 下标及dp[i] 的含义。
2. 递推公式：比如斐波那契数列 dp[i] = dp[i-1] + dp[i-2]。
3. 初始化dp数组。
4. 确定遍历顺序：从前到后or其他。
5. 推导dp数组。

出现结果不正确：

1. 打印dp日志和自己想的一样：递推公式、初始化或者遍历顺序出错。
2. 打印dp日志和自己想的不一样：代码实现细节出现问题。

416. 分割等和子集

参考文档：代码随想录

题目：

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
注意: 每个数组中的元素不会超过 100 数组的大小不会超过 200

• 示例 1:
  输入: [1, 5, 11, 5]
  输出: true
  解释: 数组可以分割成 [1, 5, 5] 和 [11].
• 示例 2:
  输入: [1, 2, 3, 5]
  输出: false
  解释: 数组不能分割成两个元素和相等的子集.
• 提示：
  1 <= nums.length <= 200
  1 <= nums[i] <= 100

分析：

dp五部曲：

1. dp[j]含义：背包重量为i时候可以装最大价值数。
2. 递推公式：dp[j] = max(dp[j], dp[j-nums[i]] + nums[i]);
3. 初始化：vector<int> dp(total+1, 0); 不能影响dp[j]的更新，设为最小自然数0。
4. 遍历顺序：双重for循环，先物品再背包，内层for循环的循环体 倒序 更新dp，适应滚动数组，不影响之前的更新，正序因为只有一个一维数组，所以会影响后面的更新。
5. 打印：
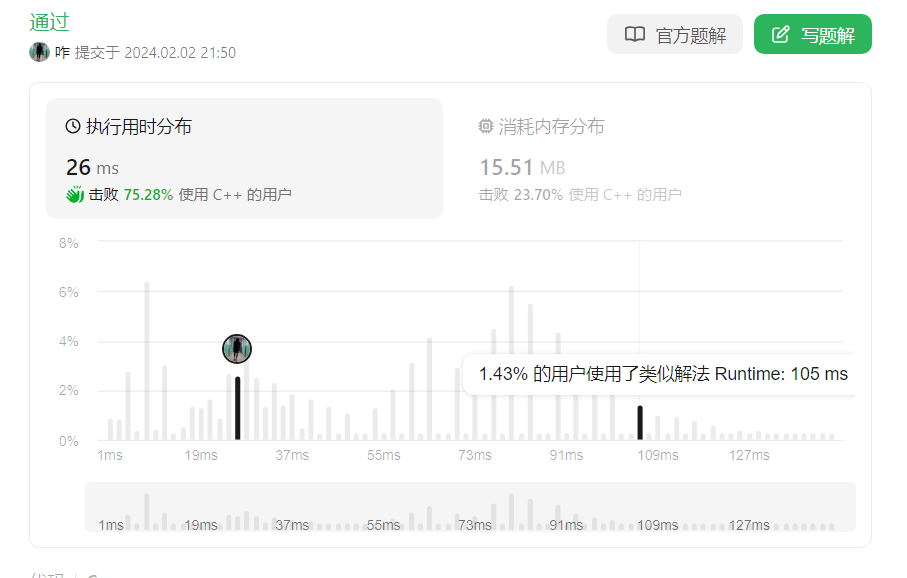
   输入: [1, 5, 11, 5]
   dp更新：
   下标值：0，1，2，3，4，5，6，7，8，9，10，11
   初始化：0，0，0，0，0，0，0，0，0，0，0，0
   i = 0 ：0，1，1，1，1，1，1，1，1，1，1，1
   i = 1 ：0，1，1，1，1，5，6，6，6，6，6，6
   i = 2 ：0，1，1，1，1，5，6，6，6，6，6，11
   i = 3 ：0，1，1，1，1，5，6，6，6，6，10，11
   代码：

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int total = 0;
        for(int i = 0; i < nums.size(); i++){
            total += nums[i];
        }
        if(total % 2) return false;
        total /= 2;// 背包的目标体积
        
        vector<int> dp(total+1, 0);

        for(int i = 0; i < nums.size(); i++){//物品个数0-nums.size()-1
            for(int j = total; j >= nums[i]; j--){//背包的体积0-total
                dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]); //递推公式
            }
        }
        if(dp[total] == total) return true;
        return false;
    }
};

二维数组实现：

1. dp[i][j]含义：从0-i的物品中任取到重量限制为j的背包得到的最大价值数。
2. 递推公式：dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i]);
3. 初始化：vector<vector<int>> dp(nums.size(), vector<int>(total+1, 0)); 第一列表示背包的重量为0时的价值为0，第一行表示在物品0存在的情况下背包不同重量的价值，满足条件的初始化为物品0的价值，其他元素都需要之后从上和左上的二维数组元素值计算得出，所以初始化值任意。
4. 遍历顺序：双重for循环，对于二维数组，先物品再背包或者先背包再物品，在当前额日伪数组求最大价值的时候上和左上元素都是存在的，所以遍历顺序任意。

先物品再背包

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int total = 0;
        for(int i = 0; i < nums.size(); i++){
            total += nums[i];
        }
        if(total % 2) return false;
        total /= 2;// 背包的目标体积
        
        //二维数组
        vector<vector<int>> dp(nums.size(), vector<int>(total+1, 0));

        for(int i = total; i >= nums[0]; i--) dp[0][i] = nums[0];

        for(int i = 1; i < nums.size(); i++){//先物品
            for(int j = 1; j <= total; j++){//再背包
                if(j < nums[i]) dp[i][j] = dp[i-1][j];
                else dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i]);
            }
        }

        if(dp[nums.size()-1][total] == total) return true;
        return false;
    }
};

先背包再物品

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int total = 0;
        for(int i = 0; i < nums.size(); i++){
            total += nums[i];
        }
        if(total % 2) return false;
        total /= 2;// 背包的目标体积
        
        //二维数组
        vector<vector<int>> dp(nums.size(), vector<int>(total+1, 0));

        for(int i = total; i >= nums[0]; i--) dp[0][i] = nums[0];

        for(int j = 1; j <= total; j++){//先背包
            for(int i = 1; i < nums.size(); i++){//再物品
                if(j < nums[i]) dp[i][j] = dp[i-1][j];
                else dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i]);
            }
        }

        if(dp[nums.size()-1][total] == total) return true;
        return false;
    }
};