1 二分法
二分法是一种分治算法,是一种数学思维。
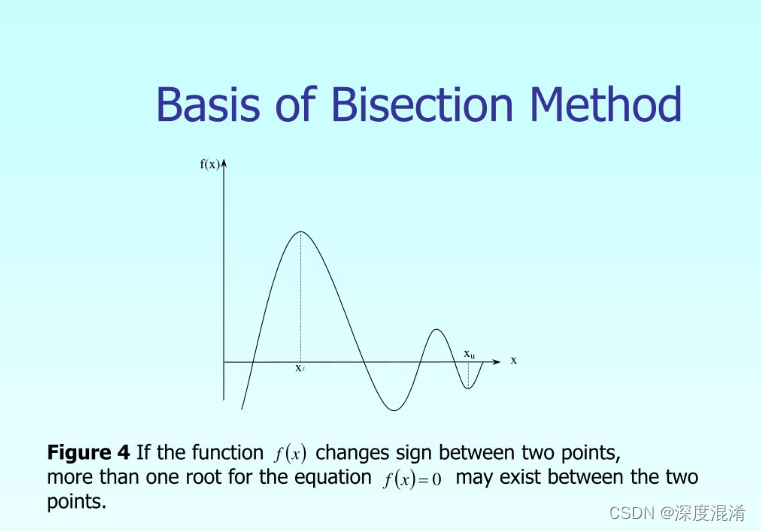
对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
基本思路:
给定精确度ξ,用二分法求函数f(x)零点近似值的步骤如下:
1 确定区间[a,b],验证f(a)·f(b)<0,给定精确度ξ.
2 求区间(a,b)的中点c.
3 计算f(c).
(1) 若f(c)=0,则c就是函数的零点;
(2) 若f(a)·f(c)<0,则令b=c;
(3) 若f(c)·f(b)<0,则令a=c.
(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.
2 代码
调用之前,请用委托方法给定需要求解的方程。
这样就可以求解任意的方程而无需修改核心代码。
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public delegate double delegateFunctionX(double x);
public static partial class Algorithm_Gallery
{
public static delegateFunctionX funx = null;
/// <summary>
/// 二分法解方程的算法
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="epsilon"></param>
/// <returns></returns>
public static double Bisection(double a, double b, double epsilon = 0.01)
{
if (funx(a) * funx(b) >= 0)
{
return 0.0;
}
double c = a;
while ((b - a) >= epsilon)
{
c = (a + b) / 2;
if (funx(c) == 0.0)
{
break;
}
else if (funx(c) * funx(a) < 0)
{
b = c;
}
else
{
a = c;
}
}
return c;
}
}
}
POWER BY TRUFFER.CN
BY 315SOFT.COM