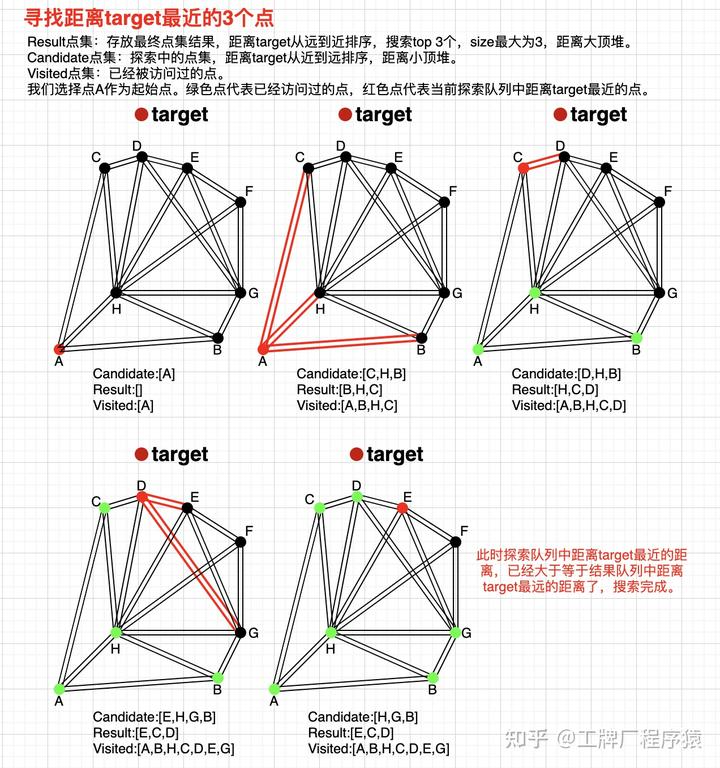
【数据结构】无向图创建邻接表以及深度遍历、广度遍历（C语言版）

news2025/1/12 0:51:11
数据结构——无向图创建邻接表以及深度遍历、广度遍历
  • 一、邻接表概念
  • 二、邻接表实现
    • （1）准备前提——结构体定义
    • （2）创建边链表
    • （3）打印边链表
    • （4）深度优先遍历
    • （5）广度优先搜索
    • （6）全部代码

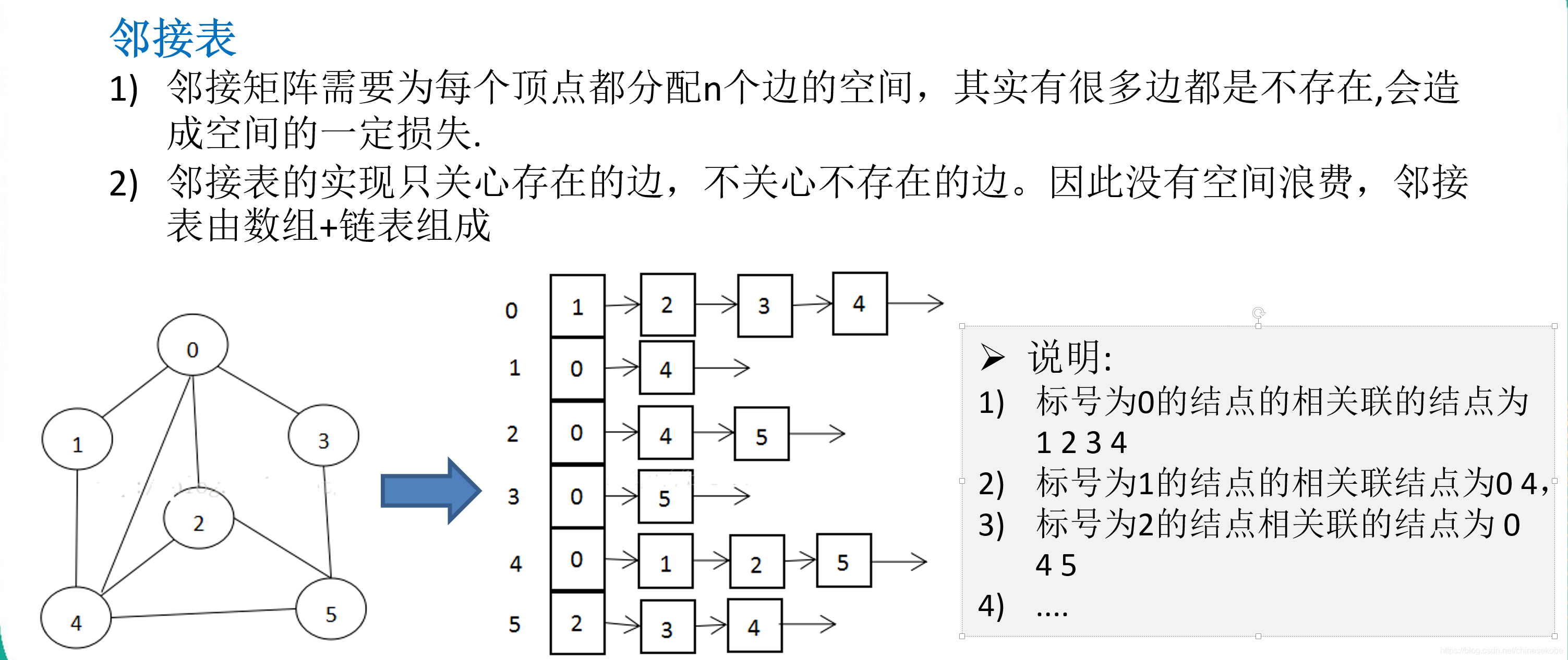
一、邻接表概念

在无向图中，顶点存储在顶点表中，以一个顶点为标记，指向边链表，两者组合在一起，称为 邻接表

  1. 对无向图的每个顶点vi建立一个单链表，第i个单链表中的结点表示依附于顶点vi的边（对于有向图则是以顶点vi为尾的弧）。这个单链表就称为顶点vi的边表（对于有向图则称为出边表）
  2. 边表的头指针和顶点的数据信息采用顺序存储（称为顶点表）
  3. 邻接表中存在两种结点：顶点表结点和边表结点
  4. 顶点表结点由顶点域（data）和指向第一条邻接边的指针（firstarc）构成
  5. 边表（邻接表）结点由邻接点域（adjvex）和指向下一条邻接边的指针域（nextarc）构成

如图：

在这里插入图片描述

在这里插入图片描述

二、邻接表实现

具体样例

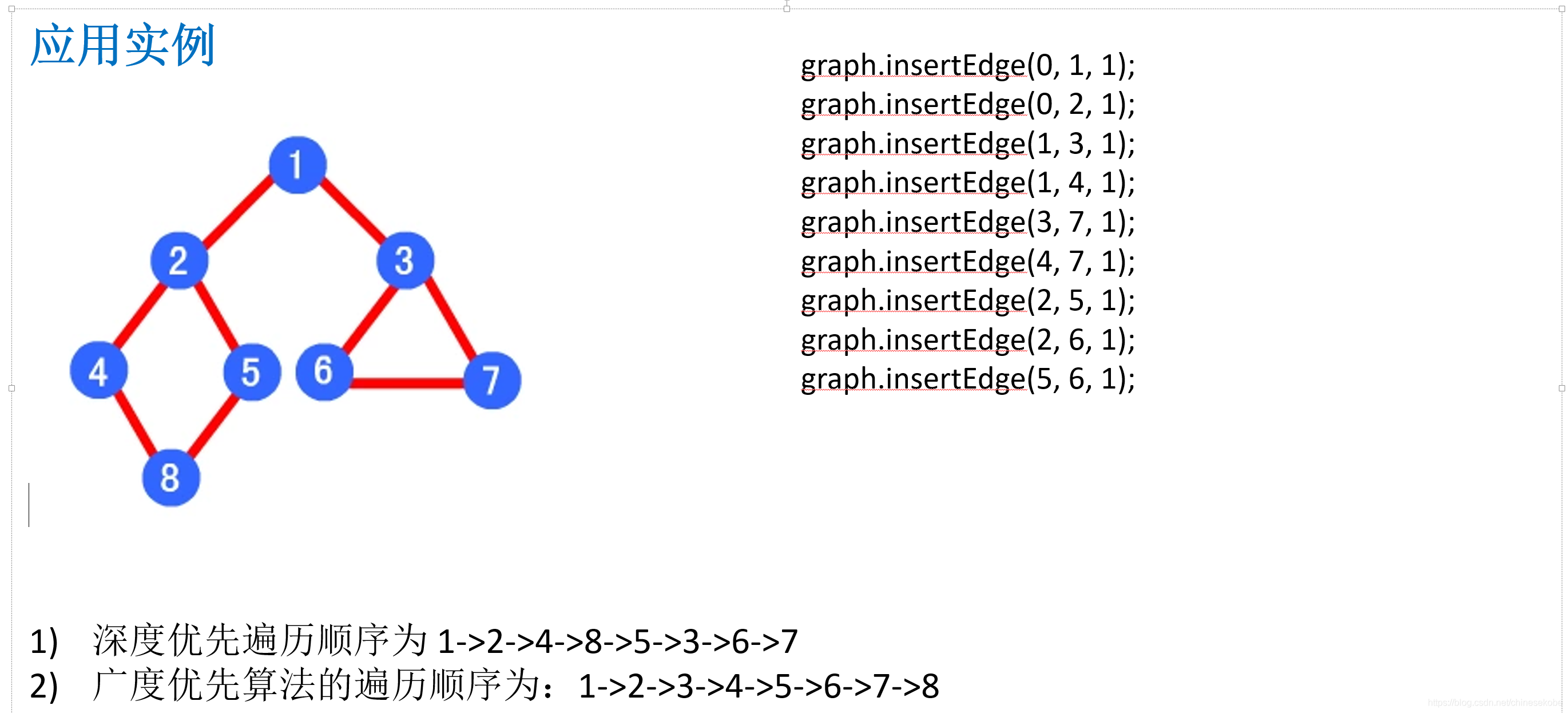
在这里插入图片描述

基本每一步，都有注释！！可认真看并理解！！！

（1）准备前提——结构体定义

#define MAXSIZE 100

//深度遍历标记数组 
int DfsVist[MAXSIZE]; 
//广度遍历标记数组 
int BfsVist[MAXSIZE];

//	边链表 
typedef struct EdgeLink{
	
	int Local;					//	存放该顶点对应边链表中数据 						 
	
	struct EdgeLink *next;		//	边链表节点指针  
	
}Edge,*ELINK;

//	顶点表 
typedef struct VertexLink{
	
	int Vertex;					//	存放一条边链表对应的顶点 
	ELINK FirstNode;			//	指向该顶点对应边链表的头节点 
	
}Vertex[MAXSIZE],*VLINK;

//	存放顶点和边，指向顶点表结构体数组 
typedef struct MyGraph{
	
	int Vnum;	//	存放顶点数 
	int Enum;	//	存放边数 
	
	Vertex List;	//	边链表对应的顶点表中顶点结构体 
	
}MyGraph;

（2）创建边链表

//	创建边链表
void CreateLink(MyGraph *T)
{
	int i,j;
	int v1,v2;
	ELINK p;		//	边链表指针 
	ELINK q;
	
	printf("请输入顶点数和边数(空格隔开):\n");
	
	scanf("%d%d",&(T->Vnum),&(T->Enum));
	
	
	//	初始化顶点表结构体数组 
	for(i=0;i<T->Vnum;i++)
	{
		printf("请输入第%d个顶点的信息:\n",i+1);
		
		scanf("%d",&(T->List[i].Vertex));		//	存放顶点在顶点表中 
		
		T->List[i].FirstNode = NULL; 		//	让每个顶点表第一个指向边链表的指针为NULL 
	}
	
	//	打印顶点坐标和顶点表中顶点数据 
	printf("---------------------------\n"); 
	for(i=0;i<T->Vnum;i++)
	{
		printf("顶点下标为:%d   顶点数据为: %d\n",i,T->List[i].Vertex); 	
	}
	printf("---------------------------\n");
	
	//	插入边链表数据	
	for(i=0;i<T->Enum;i++)
	{
		//	因为顶点表为顺序表，所以要按顶点顺序输入相连边 
		printf("请输入两个连接顶点下标(空格隔开):\n");
		
		scanf("%d%d",&v1,&v2);
		getchar(); 
		
		q = (ELINK)malloc(sizeof(Edge));	//	创建边链表节点，分配内存 
				
		q->Local = v2;	//	记录与该顶点连接边的顶点坐标
				
		q->next = NULL;						//	让尾巴指向NULL 
				
		if(!T->List[v1].FirstNode){	//	判断是否为这个顶点第一个指向的数据 
					
			T->List[v1].FirstNode = q;
					
		}else{
				//	这个顶点已经指向了一条边，以这条边为头节点，尾插法 
			p = T->List[v1].FirstNode;	//	临时存放头节点 
			while(p->next)	//	让节点指针遍历到尾巴上 
			{
				p = p->next;
			}
			p->next = q;	//	让新插的节点连接到之前边节点的尾巴上 
		}
			
		q = (ELINK)malloc(sizeof(Edge));	//	创建边链表节点，分配内存 
				
		q->Local = v1;	//	记录与该顶点连接边的顶点坐标
			
		q->next = NULL;						//	让尾巴指向NULL 
				
		if(!T->List[v2].FirstNode){	//	判断是否为这个顶点第一个指向的数据 
					
			T->List[v2].FirstNode = q;
					
		}else{
					//	这个顶点已经指向了一条边，以这条边为头节点，尾插法 
			p = T->List[v2].FirstNode;	//	临时存放头节点 
			while(p->next)	//	让节点指针遍历到尾巴上 
			{
				p = p->next;
			}
			p->next = q;	//	让新插的节点连接到之前边节点的尾巴上 
		}	
	} 
}

（3）打印边链表

//	打印邻接表 
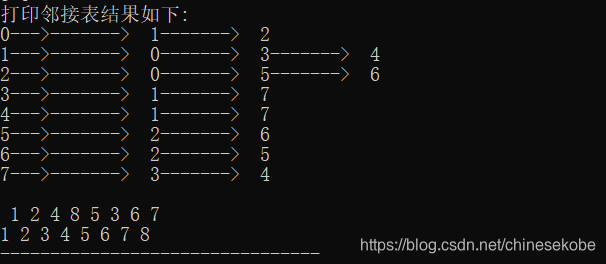
void PrintLink(MyGraph *S) 
{
	MyGraph *T = S;
	ELINK Q;			//	防止边链表指针指到NULL ，用临时指针代替遍历打印 
		
	int i;
	printf("打印邻接表结果如下:\n");
	for(i=0;i<T->Vnum;i++)
	{
		Q = T->List[i].FirstNode;	//	接受每个顶点指向对应边链表的头节点指针 
		printf("%d--->",i);
		
		while(1)
		{
			if(Q == NULL)	//	指针指到尾巴 NULL
			{
				putchar('\n');
				break;
			}
			printf("------->%3d",Q->Local);
			
			Q = Q->next;	
		}
	}
	putchar('\n');
}

（4）深度优先遍历

//*****************	深度优先遍历算法—邻接表 *****************//
void DFS_Link(MyGraph *T,int n)
{	
	int i,j;
	ELINK q;	//	指向边链表节点指针 
	
	if(n<0 || n>=T->Vnum)
	{
		printf("输入有误\n");
		return;	
	}
		DfsVist[n] = 1;		//	遍历一个顶点，做下标记 1  

		printf(" %d",T->List[n].Vertex);
		
		q = T->List[n].FirstNode;	//q指向下标为i所对顶点 对应的边链表的第一个边结点	
		
		while(q!=NULL)	
		{	
			if(DfsVist[q->Local]!=1)
			{
			
				j = q->Local;
				DFS_Link(T,j);
			} 
			
			q = q->next;
		} 
} 
//	初始化深度遍历—邻接表 
void Init_DFSLINK(MyGraph *Q)
{
	int i;
	for(i=0;i<Q->Vnum;i++)
	{
		DfsVist[i] = 0;
	}
		
	for(i=0;i<Q->Vnum;i++)
	{
		if(!DfsVist[i])
		{
		 DFS_Link(Q,i);	//	此顶点没有被标记，开始递归遍历
		}
	}
	putchar('\n'); 
}

（5）广度优先搜索

//	广度遍历 
void BFS(MyGraph *S,int t)
{
	ELINK P; 			//	指向顶点所对应的边链表中 
	
	int i;
	int v;		//	用来接收边链表对应的顶点
	
	
	//	创建一个数组队列 
	int Queue[MAXSIZE];
	int front = 0;			//	队头 
	int rear = 0;			//	队尾 
		
	printf("%d ",S->List[t].Vertex);	//	输出当前遍历边链表的顶点 
	BfsVist[t] = 1;		//	将该顶点作标记
	
	rear = (rear+1)%MAXSIZE;	//	入队一个让队尾指向后移一位
	Queue[rear] = t;	 		//	将该顶点入队 

	while(front != rear)	//	若front == rear，表明这个顶点在边链表上连接的顶点已经遍历完毕 
	{
		front = (front+1)%MAXSIZE;		//	出队 
	
		v = Queue[front];			//	得到此时遍历到顶点坐标 
		
		P = S->List[v].FirstNode;	//	遍历当前顶点指向边链表中连接的其他顶点
									//	也就是换个顶点的边链表继续遍历查找剩余顶点 
		while(P!=NULL)
		{
			
			if(BfsVist[P->Local] == 0)
			{			
				printf("%d ",P->Local+1);	//	输出连接边顶点 
				
				BfsVist[P->Local] = 1;		//	作标记,表示这个顶点已经搜索过 
				
				rear = (rear+1)%MAXSIZE;		//	将该下标入队 
				
				Queue[rear] = P->Local;	//	把遍历到新的边链表对应的顶点坐标入队 
			}
			
			P = P->next;	//	遍历这个顶点的边链表 
		}	
	} 
} 

//	BFS广度遍历初始化
void Init_BFS(MyGraph *S)
{
	int i;
	
	for(i=0;i<S->Vnum;i++)
	{
		BfsVist[i] = 0;	//	初始化标记符 
	}
	
	for(i=0;i<S->Vnum;i++)
	{
		if(BfsVist[i]==0)
			BFS(S,i);
	}	
}

（6）全部代码

#include<stdio.h>
#include<stdlib.h>

#define MAXSIZE 100

//深度遍历标记数组 
int DfsVist[MAXSIZE]; 
//广度遍历标记数组 
int BfsVist[MAXSIZE];

//	边链表 
typedef struct EdgeLink{
	
	int Local;					//	存放该顶点对应边链表中数据 						 
	
	struct EdgeLink *next;		//	边链表节点指针  
	
}Edge,*ELINK;

//	顶点表 
typedef struct VertexLink{
	
	int Vertex;					//	存放一条边链表对应的顶点 
	ELINK FirstNode;			//	指向该顶点对应边链表的头节点 
	
}Vertex[MAXSIZE],*VLINK;

//	存放顶点和边，指向顶点表结构体数组 
typedef struct MyGraph{
	
	int Vnum;	//	存放顶点数 
	int Enum;	//	存放边数 
	
	Vertex List;	//	边链表对应的顶点表中顶点结构体 
	
}MyGraph;

//	创建边链表
void CreateLink(MyGraph *T)
{
	int i,j;
	int v1,v2;
	ELINK p;		//	边链表指针 
	ELINK q;
	
	printf("请输入顶点数和边数(空格隔开):\n");
	
	scanf("%d%d",&(T->Vnum),&(T->Enum));
	
	
	//	初始化顶点表结构体数组 
	for(i=0;i<T->Vnum;i++)
	{
		printf("请输入第%d个顶点的信息:\n",i+1);
		
		scanf("%d",&(T->List[i].Vertex));		//	存放顶点在顶点表中 
		
		T->List[i].FirstNode = NULL; 		//	让每个顶点表第一个指向边链表的指针为NULL 
	}
	
	//	打印顶点坐标和顶点表中顶点数据 
	printf("---------------------------\n"); 
	for(i=0;i<T->Vnum;i++)
	{
		printf("顶点下标为:%d   顶点数据为: %d\n",i,T->List[i].Vertex); 	
	}
	printf("---------------------------\n");
	
	//	插入边链表数据	
	for(i=0;i<T->Enum;i++)
	{
		//	因为顶点表为顺序表，所以要按顶点顺序输入相连边 
		printf("请输入两个连接顶点下标(空格隔开):\n");
		
		scanf("%d%d",&v1,&v2);
		getchar(); 
		
		q = (ELINK)malloc(sizeof(Edge));	//	创建边链表节点，分配内存 
				
		q->Local = v2;	//	记录与该顶点连接边的顶点坐标
				
		q->next = NULL;						//	让尾巴指向NULL 
				
		if(!T->List[v1].FirstNode){	//	判断是否为这个顶点第一个指向的数据 
					
			T->List[v1].FirstNode = q;
					
		}else{
				//	这个顶点已经指向了一条边，以这条边为头节点，尾插法 
			p = T->List[v1].FirstNode;	//	临时存放头节点 
			while(p->next)	//	让节点指针遍历到尾巴上 
			{
				p = p->next;
			}
			p->next = q;	//	让新插的节点连接到之前边节点的尾巴上 
		}
			
		q = (ELINK)malloc(sizeof(Edge));	//	创建边链表节点，分配内存 
				
		q->Local = v1;	//	记录与该顶点连接边的顶点坐标
			
		q->next = NULL;						//	让尾巴指向NULL 
				
		if(!T->List[v2].FirstNode){	//	判断是否为这个顶点第一个指向的数据 
					
			T->List[v2].FirstNode = q;
					
		}else{
					//	这个顶点已经指向了一条边，以这条边为头节点，尾插法 
			p = T->List[v2].FirstNode;	//	临时存放头节点 
			while(p->next)	//	让节点指针遍历到尾巴上 
			{
				p = p->next;
			}
			p->next = q;	//	让新插的节点连接到之前边节点的尾巴上 
		}	
	} 
}

//	打印邻接表 
void PrintLink(MyGraph *S) 
{
	MyGraph *T = S;
	ELINK Q;			//	防止边链表指针指到NULL ，用临时指针代替遍历打印 
		
	int i;
	printf("打印邻接表结果如下:\n");
	for(i=0;i<T->Vnum;i++)
	{
		Q = T->List[i].FirstNode;	//	接受每个顶点指向对应边链表的头节点指针 
		printf("%d--->",i);
		
		while(1)
		{
			if(Q == NULL)
			{
				putchar('\n');
				break;
			}
			printf("------->%3d",Q->Local);
			
			Q = Q->next;	//！！BUG 
		}
	}
	putchar('\n');
}

//*****************	深度优先遍历算法—邻接表 *****************//
void DFS_Link(MyGraph *T,int n)
{	
	int i,j;
	ELINK q;	//	指向边链表节点指针 
	
	if(n<0 || n>=T->Vnum)
	{
		printf("输入有误\n");
		return;	
	}
		DfsVist[n] = 1;		//	遍历一个顶点，做下标记 1  

		printf(" %d",T->List[n].Vertex);
		
		q = T->List[n].FirstNode;	//q指向下标为i所对顶点 对应的边链表的第一个边结点	
		
		while(q!=NULL)	
		{	
			if(DfsVist[q->Local]!=1)
			{
			
				j = q->Local;
				DFS_Link(T,j);
			} 
			
			q = q->next;
		}	 
} 

//	初始化深度遍历—邻接表 
void Init_DFSLINK(MyGraph *Q)
{
	int i;
	for(i=0;i<Q->Vnum;i++)
	{
		DfsVist[i] = 0;
	}
		
	for(i=0;i<Q->Vnum;i++)
	{
		if(!DfsVist[i])
		{
		 DFS_Link(Q,i);	//	此顶点没有被标记，开始递归遍历
		}
	}
	putchar('\n'); 	
}

//	广度遍历 
void BFS(MyGraph *S,int t)
{
	ELINK P; 			//	指向顶点所对应的边链表中 
	
	int i;
	int v;		//	用来接收边链表对应的顶点
	
	//	为了不和广度搜素—邻接矩阵冲突
	//	创建一个数组队列 
	int Queue[MAXSIZE];
	int front = 0;			//	队头 
	int rear = 0;			//	队尾 
		
	printf("%d ",S->List[t].Vertex);	//	输出当前遍历边链表的顶点 
	BfsVist[t] = 1;		//	将该顶点作标记
	
	rear = (rear+1)%MAXSIZE;	//	入队一个让队尾指向后移一位
	Queue[rear] = t;	 		//	将该顶点入队 

	while(front != rear)	//	若front == rear，表明这个顶点在边链表上连接的顶点已经遍历完毕 
	{
		front = (front+1)%MAXSIZE;		//	出队 
	
		v = Queue[front];			//	得到此时遍历到顶点坐标 
		
		P = S->List[v].FirstNode;	//	遍历当前顶点指向边链表中连接的其他顶点
									//	也就是换个顶点的边链表继续遍历查找剩余顶点 
		while(P!=NULL)
		{
			
			if(BfsVist[P->Local] == 0)
			{			
				printf("%d ",P->Local+1);	//	输出连接边顶点 
				
				BfsVist[P->Local] = 1;		//	作标记,表示这个顶点已经搜索过 
				
				rear = (rear+1)%MAXSIZE;		//	将该下标入队 
				
				Queue[rear] = P->Local;	//	把遍历到新的边链表对应的顶点坐标入队 
			}
			
			P = P->next;	//	遍历这个顶点的边链表 
		}	
	} 
} 

//	BFS广度遍历初始化
void Init_BFS(MyGraph *S)
{
	int i;
	
	for(i=0;i<S->Vnum;i++)
	{
		BfsVist[i] = 0;	//	初始化标记符 
	}
	
	for(i=0;i<S->Vnum;i++)
	{
		if(BfsVist[i]==0)
			BFS(S,i);
	}
} 

int main()
{
	MyGraph *S;
	S = (MyGraph *)malloc(sizeof(MyGraph));
	
	//	创建边链表 
	CreateLink(S);
	
	//	打印边链表 
	PrintLink(S);
	
	//	深度遍历
	Init_DFSLINK(S); 
	
	//	广度遍历 
	Init_BFS(S);
	 
	return 0;	
}

运行结果：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1451173.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

前端可能需要的一些安装

前端可能需要的一些安装

Node.js Node.js 官网 Node.js 中文网 Node.js is an open-source, cross-platform JavaScript runtime environment. Node.js是一个开源、跨平台的JavaScript运行时环境。Recommended for most users 推荐大多数用户使用哔哩哔哩安装视频 安装 node.js 的时候&#xff0c;会…
阅读更多...
安卓TextView 拖动命名

安卓TextView 拖动命名

需求&#xff1a;该布局文件使用线性布局来排列三个文本视图和一个按钮&#xff0c;分别用于显示两个动物名称以及占位文本视图。在占位文本视图中&#xff0c;我们为其设置了背景和居中显示样式&#xff0c;并用其作为接收拖放操作的目标 效果图&#xff1b; 实现代码 第一布…
阅读更多...
如何解决缓存和数据库的数据不一致问题

如何解决缓存和数据库的数据不一致问题

数据不一致问题是操作数据库和操作缓存值的过程中&#xff0c;其中一个操作失败的情况。实际上&#xff0c;即使这两个操作第一次执行时都没有失败&#xff0c;当有大量并发请求时&#xff0c;应用还是有可能读到不一致的数据。 如何更新缓存 更新缓存的步骤就两步&#xff0…
阅读更多...
【C++】---类和对象（中）默认成员函数 和 操作符重载

【C++】---类和对象（中）默认成员函数 和 操作符重载

前言&#xff1a; 假如一个类中既没有成员变量也没有成员函数&#xff0c;那么这个类就是空类&#xff0c;空类并不是什么都没有&#xff0c;因为所有类都会生成如下6个默认成员函数&#xff1a; 一、构造函数 1、构造函数的定义及其特性 对于日期类对象&#xff0c;我们可…
阅读更多...
C语言---指针进阶

C语言---指针进阶

1.字符指针 int main() {char str1[] "hello world";char str2[] "hello world";const char* str3 "hello world.";const char* str4 "hello world.";if (str3 str4){//常量字符串在内存里面是无法修改的&#xff0c;所以没必要…
阅读更多...
数据检索：倒排索引加速、top-k和k最邻近

数据检索：倒排索引加速、top-k和k最邻近

之前在https://www.yuque.com/treblez/qksu6c/wbaggl2t24wxwqb8?singleDoc# 《Elasticsearch: 非结构化的数据搜索》我们看了ES的设计&#xff0c;主要侧重于它分布式的设计以及LSM-Tree&#xff0c;今天我们来关注算法部分&#xff1a;如何进行检索算法的设计以及如何加速倒排…
阅读更多...
RapidMiner数据挖掘2 —— 初识RapidMiner

RapidMiner数据挖掘2 —— 初识RapidMiner

本节由一系列练习与问题组成&#xff0c;这些练习与问题有助于理解多个基本概念。它侧重于各种特定步骤&#xff0c;以进行直接的探索性数据分析。因此&#xff0c;其主要目标是测试一些检查初步数据特征的方法。大多数练习都是关于图表技术&#xff0c;通常用于数据挖掘。 为此…
阅读更多...
嵌入式系统中常见传感器介绍

嵌入式系统中常见传感器介绍

&#xff08;本文为简单介绍&#xff0c;内容取材网络&#xff09; 传感器是嵌入式系统接入外部环境信息的重要接口,根据测量物理量的不同,传感器可以分为温度传感器、湿度传感器、压力传感器、加速度传感器等多种类型。选择合适的传感器,对于实现嵌入式系统的控制和互动功能至…
阅读更多...
Java微服务架构的选择：Spring Cloud、Kubernetes还是Kubernetes + Istio？

Java微服务架构的选择：Spring Cloud、Kubernetes还是Kubernetes + Istio？

微服务架构已经成为现代软件开发的趋势&#xff0c;其可以带来高度可伸缩性、松耦合性和团队自治性等优势。 在Java开发领域中&#xff0c;选择适合的微服务架构是非常关键的决策&#xff0c;本文将探讨Spring Cloud、Kubernetes和KubernetesIstio这三个架构选择的优势和劣势。…
阅读更多...
MIT-BEVFusion系列八--onnx导出1 综述及相机网络导出

MIT-BEVFusion系列八--onnx导出1 综述及相机网络导出

目录 综述export-camera.py加载模型加载数据生成需要导出成 onnx 的模块Backbone 模块VTransform 模块 生成 onnx使用 pytorch 原生的伪量化计算方法导出 camera.backbone.onnx导出 camera.vtransform.onnx 综述 bevfusion的各个部分的实现有着鲜明的特点&#xff0c;并且相互…
阅读更多...
BUGKU-WEB 本地管理员

BUGKU-WEB 本地管理员

题目描述 题目截图如下&#xff1a; 进入场景看看&#xff1a; 解题思路 老规矩&#xff0c;先看源码发现了&#xff0c;那就要base一下了测试账号密码绕过IP限制 相关工具 F12插件modHeader 或者 直接使用Burp Suit对请求进行修改 解题步骤 先输入admin测试一下 显示…
阅读更多...
vue3 中使用pinia 数据状态管理(在Taro 京东移动端框架中的使用)

vue3 中使用pinia 数据状态管理(在Taro 京东移动端框架中的使用)

1.pinia 介绍 pinia 是 Vue 的存储库&#xff0c;它允许您跨组件/页面共享状态。就是和vuex一样的实现数据共享。 依据Pinia官方文档&#xff0c;Pinia是2019年由vue.js官方成员重新设计的新一代状态管理器&#xff0c;更替Vuex4成为Vuex5。 Pinia 目前也已经是 vue 官方正式的…
阅读更多...
蓝桥杯2023年第十四届省赛真题

蓝桥杯2023年第十四届省赛真题

题目 题目描述&#xff1a; 程序猿圈子里正在流行一种很新的简写方法&#xff1a;对于一个字符串&#xff0c;只保留首尾字符&#xff0c;将首尾字符之间的所有字符用这部分的长度代替。例如 internation-alization 简写成 i18n&#xff0c;Kubernetes &#xff08;注意连字符不…
阅读更多...
Javaweb之SpringBootWeb案例之AOP核心概念的详细解析

Javaweb之SpringBootWeb案例之AOP核心概念的详细解析

2.3 AOP核心概念 通过SpringAOP的快速入门&#xff0c;感受了一下AOP面向切面编程的开发方式。下面我们再来学习AOP当中涉及到的一些核心概念。 1. 连接点&#xff1a;JoinPoint&#xff0c;可以被AOP控制的方法&#xff08;暗含方法执行时的相关信息&#xff09; 连接点指的…
阅读更多...
2.8学习总结

2.8学习总结

2.8 1.二叉树的前序遍历 2.二叉树的中序遍历 3.二叉树的后序遍历 4.⼆叉树的层序遍历 5.⼆叉树的层序遍历2 6.二叉树的右视图 7.二叉树的层平均值 8.N叉树的层序遍历 9.每个树行中找最大值 10.填充每个节点的下一个右侧节点指针 11.填充每个节点的下一个右侧节点指针2 12.生命之…
阅读更多...
C/C++中的max函数如何使用？哪个头文件？多个数字可以用max吗？

C/C++中的max函数如何使用？哪个头文件？多个数字可以用max吗？

在C中&#xff0c;max函数是一个非常实用的函数&#xff0c;它用于比较两个或更多数值并返回其中的最大值。这个函数在头文件中定义。 下面是如何在C中使用max函数的一些示例&#xff1a; #include <iostream> #include <algorithm> // 引入algorithm头文件以使…
阅读更多...
【从Python基础到深度学习】 8. VIM两种状态

【从Python基础到深度学习】 8. VIM两种状态

一、安装 sudo apt install vim 二、VIM两种模式 - 命令状态/编辑状态 1.1 进入/退出VIM 进入VIM vim 退出vim :q <enter> 2.2 根目录下添加配置文件 window下创建vimrc类型文件内容如下&#xff1a; set nu set cursorline set hlsearch set tabstop4 使用Wins…
阅读更多...
HTTP协议-响应报文详解（Respond）

HTTP协议-响应报文详解（Respond）

目录 前言&#xff1a; 1.Respond报文 1.1报文格式 1.2格式图解 2.状态行&#xff08;首行&#xff09; 2.1状态码/状态码解释 &#xff08;1&#xff09;200 OK &#xff08;2&#xff09;404 Not Found &#xff08;3&#xff09;403 Forbidden &#xff08;4&#…
阅读更多...
【LeetCode: 107. 二叉树的层序遍历 II + BFS】

【LeetCode: 107. 二叉树的层序遍历 II + BFS】

&#x1f680; 算法题 &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&#xff0c;…
阅读更多...
红队笔记Day4 --＞多层代理（模拟企业拓扑）

红队笔记Day4 --＞多层代理（模拟企业拓扑）

声明&#xff1a;本机文章只用于教育用途&#xff0c;无不良引导&#xff0c;禁止用于从事任何违法活动 前几天的红队笔记的网络拓扑都比较简单&#xff0c;今天就来模拟一下企业的真实网络拓扑&#xff0c;以及攻击方法 一般的大企业的网络拓扑如下&#xff1a;&#xff1a;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023