差分其实就是前缀和的逆运算。
如果数组 A 是数组 B 的前缀和数组,则称 B 是 A 的差分数组。
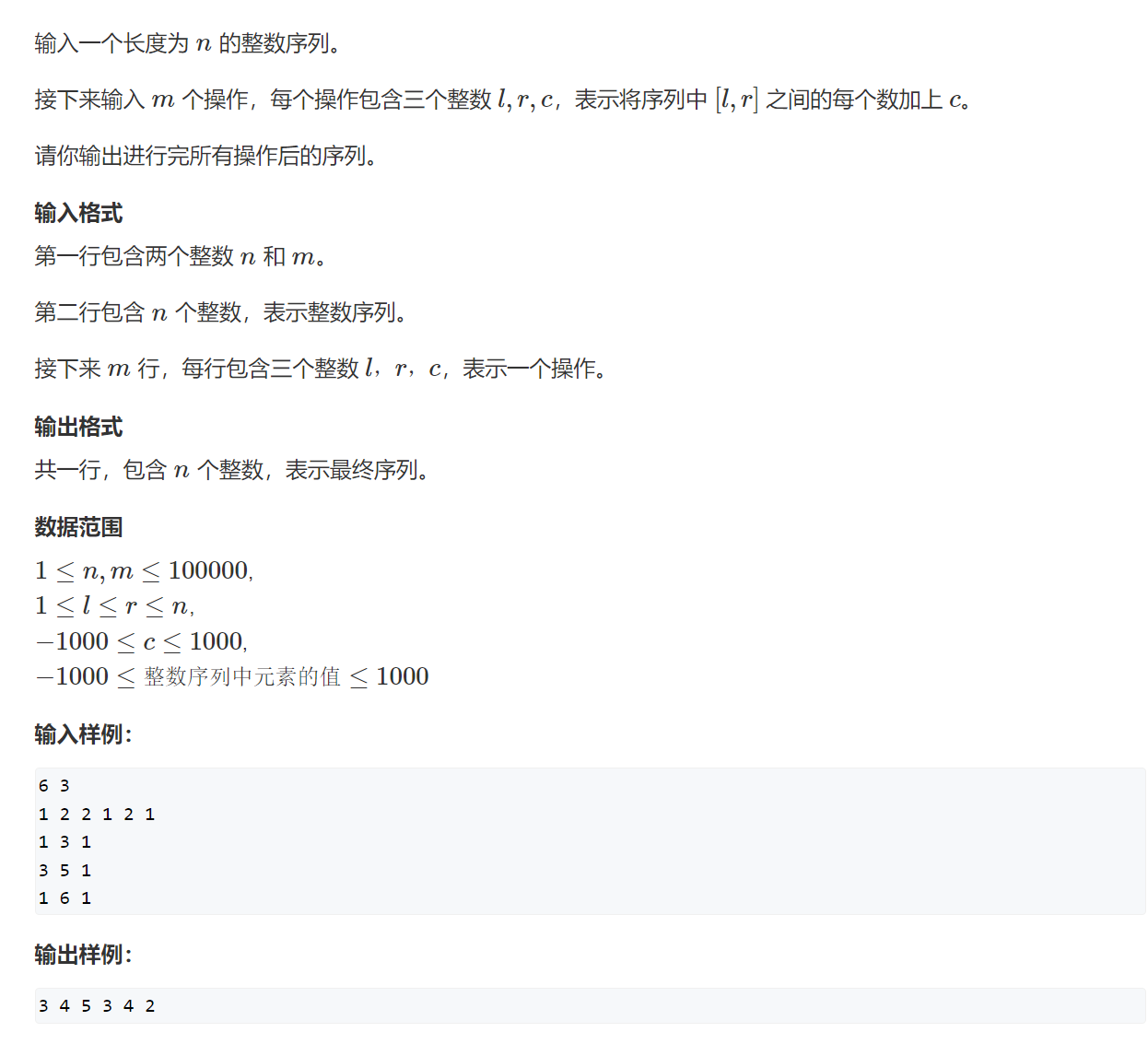
思路
由题意得,应该求给定数组的差分数组。
差分加速的原理
对 L 到 R 区间内的数加上 c,时间复杂度是O(c) ,即O(n) 。
但是如果应用差分数组来执行这个操作,由于 A 是 B 的前缀和,因此执行下列语句:
B[L] += c;
B[R+1] -= c;就可以实现,时间复杂度为O(2) ,一般称为O(1)。
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[100010];
int b[100010];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;++i)
{
cin>>a[i];
b[i] += a[i]; // 注意这里初始化b数组的方法
b[i+1] -= a[i];
}
int l, r, c;
for(int i=1;i<=m;++i)
{
cin>>l>>r>>c;
b[l] += c;
b[r+1] -= c;
}
for(int i=1;i<=n;++i)
{
b[i] += b[i-1]; // 求前缀和,也就得到了最终的a数组
cout<<b[i]<<' ';
}
return 0;
}