1. 为什么需要transformer
循环模型通常沿输入和输出序列的符号位置进行因子计算。通过在计算期间将位置与步骤对齐,它们根据前一步的隐藏状态和输入产生位置
的隐藏状态序列
。这种固有的顺序特性阻止了训练样本内的并行化,这在较长的序列长度上变得至关重要,因为有限的内存限制了样本的批处理大小。
相较于seq2seq结构每个时间步的输出需要依赖于前面时间步的输出,这使得模型没有办法并行,效率低,面临对齐问题,Transformer 模型规避了循环而完全只依赖于注意力机制,为输入和输出序列刻画全局的依赖信息。下面是 transformer 的架构图。
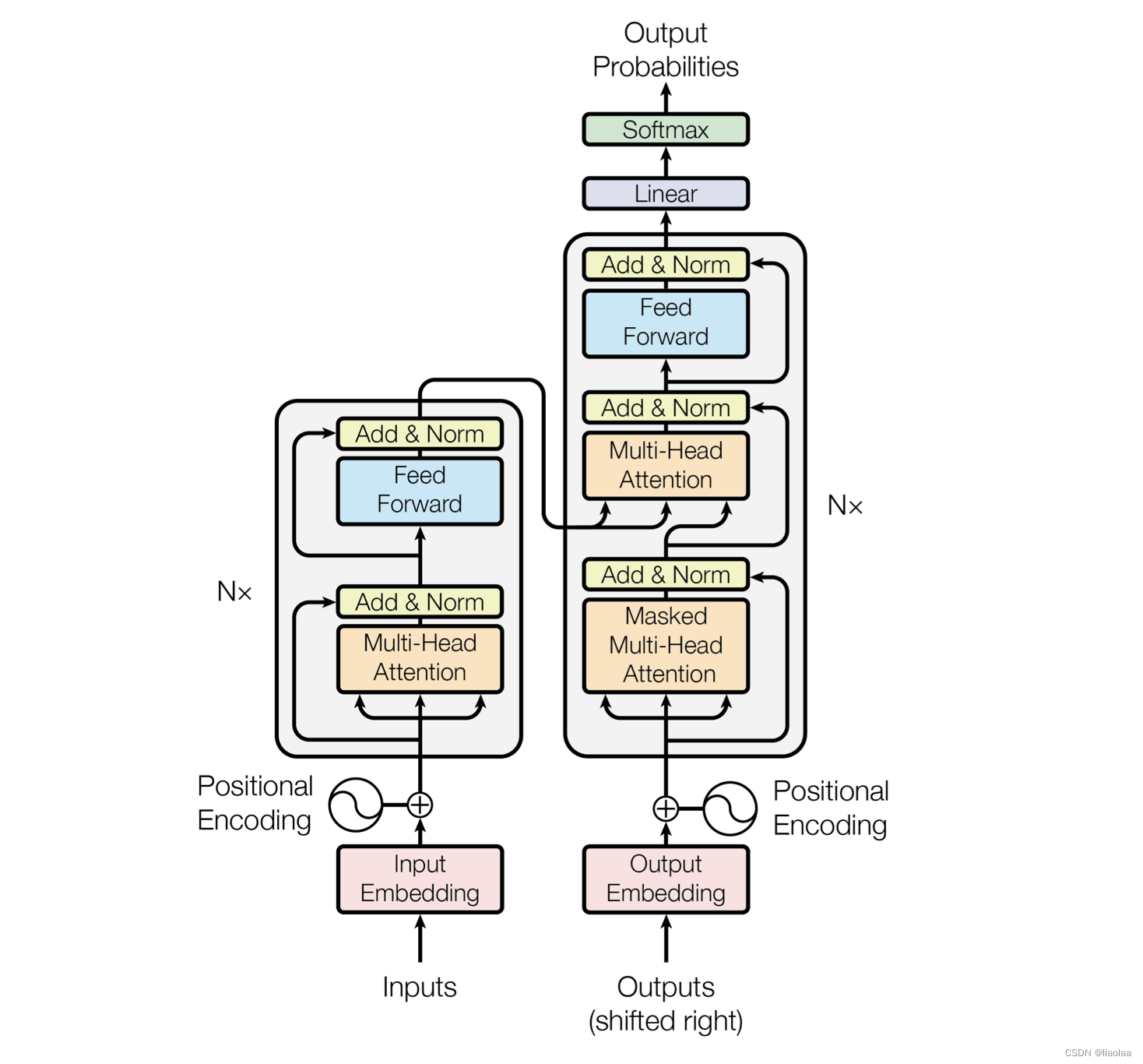
2. 嵌入层
2.1 位置编码(positional encodings)
由于 transformer 不包含循环和卷积,为了让模型利用序列的顺序,我们必须注入序列中关于词符相对或者绝对位置的一些信息。为此,我们将位置编码和词嵌入后的结果相加,作为编码器和解码器堆栈底部的输入。

其中 i 是维度索引,pos 是位置索引,d_model 是词嵌入的维度,在偶数维和奇数维分别采用正弦波和余弦波编码 。最后会将词嵌入和位置编码相加作为编码器、解码器的输入。
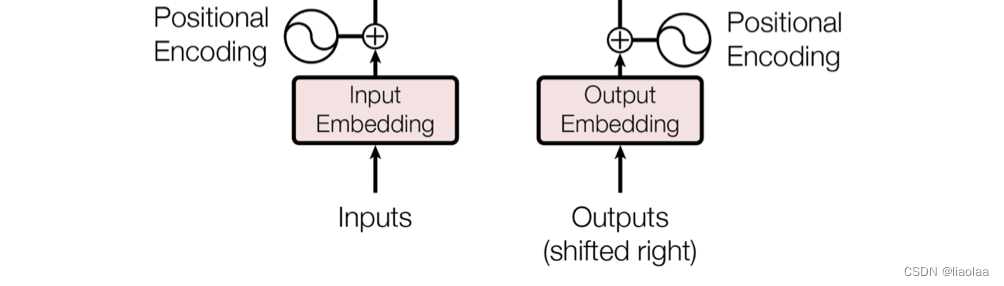
2.2 嵌入层的实现
# transform中的两个词嵌入层都是一样的,即两个词嵌入层共享参数
class Embeddings(nn.Module):
def __init__(self, d_model, vocab_size):
super(Embeddings, self).__init__()
self.emb = nn.Embedding(num_embeddings=vocab_size, embedding_dim=d_model)
self.d_model = d_model
def forward(self, x):
return self.emb(x) * math.sqrt(self.d_model)
# 位置编码
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.5, max_len=500):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# 初始化一个位置编码矩阵 [max_len, d_model]
pe = torch.zeros(max_len, d_model)
# 初始化一个绝对位置矩阵,词汇的绝对位置就是用行索引表示
position = torch.arange(0, max_len).unsqueeze(1) # [max_len, 1]
# 将绝对位置矩阵的位置信息加入到位置编码矩阵中
# 进行矩阵变换,把数值缩放,以便于后续训练更快的收敛
# 将矩阵按照奇偶一分为二,奇数位置用正弦波编码,偶数位置用余弦波编码
div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(1000.0)/d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term) # [max_len, d_model]
# 要和embedding结果相加需要对维度做调整,即
# [max_len, d_model] -> [batch_size, max_len, d_model]
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
"""
:param x: embedding后的结果(文本序列的词嵌入表示),为 [batch_size, seq_len, d_model]
:return:
"""
x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
return self.dropout(x)3. transformer中的编码器层
3.1 编码器层
编码器层完成一次对输入的特征提取过程,即编码过程。

编码器是由N层完全相同编码器层堆叠起来的,每层包括两个子层连接结构:
1. 第一个子层连接结构是一个多头注意力子层和一个规范化层和残差连接的组合;
2. 第二个子层连接结构是一个前馈全连接子层和一个规范化层和残差连接的组合。
3.2 掩码张量
3.2.1 什么是掩码张量
掩码张量是一个尺寸不固定的的张量,里面只包含0或1两种值,表示遮掩和不遮掩(也可以是不遮掩和遮掩),把其他张量的对应位置上的值遮掩住。
3.2.2 掩码张量的作用
用来遮掩一些当前时间步不能看见的信息,在生成的attention张量中的值计算可能看到了未来时间步的信息而得到的,未来时间步信息被看到是因为训练的时候会把整个输出结果都一次性进行embedding,但在解码器的输出却不是一次能产生最终结果的,而是循环生成的,因此为了防止未来时间步的信息被看到所以我们需要用到掩码张量。
3.2.3 掩码张量的实现
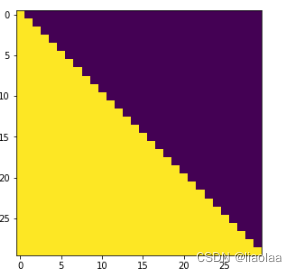
看上面这张图,横坐标为目标词的序列,纵坐标为可知信息的序列,黄色代表被遮掩,紫色是未被遮掩。在解码器生成序列的第一个时间步中,我们看不到任何信息,因此在横轴为0的时候信息是全被遮掩的,在第二个时间步的时候,可以看到第一个时间步的输出,因此在横轴为1的位置上可以看到第一个时间步的输出信息,同理后续的时间步也是如此。
所以mask应该为一个下三角矩阵,如下:
def subsequence_mask(seq_len, batch_size=1):
"""
生成向后遮掩的掩码张量,遮掩未来时间步的信息
:param seq_len: mask矩阵的大小 [seq_len, seq_len]
:return:
"""
# 生成一个上三角阵
subsequence_mask = np.triu(np.ones((batch_size, seq_len, seq_len)), k=1).astype('uint8') # [batch_size, seq_len, seq_len]
return torch.from_numpy(1 - subsequence_mask) # 下三角全1矩阵
if __name__ == '__main__':
print(subsequence_mask(seq_len=5))
# tensor([[[1, 0, 0, 0, 0],
# [1, 1, 0, 0, 0],
# [1, 1, 1, 0, 0],
# [1, 1, 1, 1, 0],
# [1, 1, 1, 1, 1]]], dtype=torch.uint8)
通过mask使得解码器不能看见未来的信息。也就是对于一个序列,我们的解码输出应该只能依赖于当前时间步之前的输出。因为我们通常都是取一个batch的数据,所以我们的mask直接做成三维的,第一个维度为batch_size的。
3.3 Attention子层
3.3.1 如何理解Attention中的Q,K,V
举个例子,我们在做阅读理解的时候,我们可以根据某一段话归纳出中心思想,问题题干会附带上关键词,这个关键词就是Key,这段话就是Query,我们带着这些关键词Key去阅读这一段话Query,我们理解到的信息就是Value。我们在一开始的时候对这段话理解不深,理解到的信息很少基本上是关键词Key给我们的信息,所以此时的Value和Key值会很相似,随着我们阅读次数的增加,我们对文本Query的理解加深,从中提取到的信息越来越多,我们的Value值会不断变化,最终根据学习能力的不同我们得到的Value值会和参考答案相近甚至一样。
上述过程就是注意力作用的过程,根据Key生成了Query的关键词表示方法。我们上面所说的这种情况是Key值和Value值相同,与Query不同,根据不同于给定文本的关键词表示文本。另外一种情况是Key值、Value值和Query值都相同,这个就是自注意力机制。自注意力根据给定的文本自身来表示文本,即从给定文本中提取关键词来表示文本。
3.3.2 计算自注意力(Scaled Dot-Product Attention)

根据论文原文描述,我们可以把querys,keys和values分别打包成三个Q,K和V矩阵,将Q矩阵和K矩阵做点积(这里是为了得到querys和keys之间的相似度)再经过softmax得到一个分数矩阵,也就是V矩阵的权重,再于V矩阵相乘得到最终的结果。这里有个问题,如果没有加上缩放因子,在点积结果大幅度增长的情况下,将 softmax 函数推向具有极小梯度的区域。因此加上了缩放因子,即Scale的步骤。
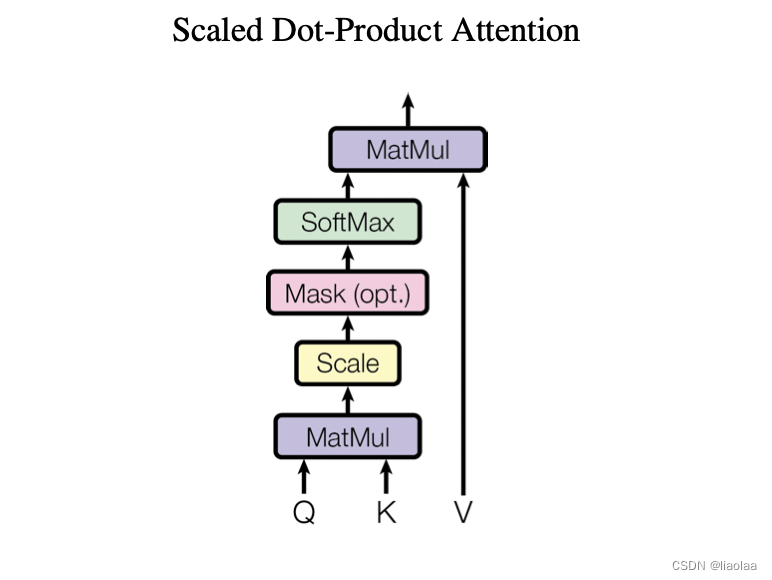
因为直接把所有信息打包成矩阵输入进去做attention,所以在softmax之前我们还需要通过Mask操作把未来时间步信息遮掩起来。
3.3.3 自注意力的实现
def attention(query, key, value, mask=None, dropout=None):
"""
:param query: [batch_size, seq_len, d_model]
:param key: [batch_size, seq_len, d_model]
:param value: [batch_size, seq_len, d_model]
:param mask:
:param dropout:
:return: attention后的value,和注意力矩阵
"""
d_k = query.size(-1) # 词嵌入维度
scores = torch.matmul(query,key.transpose(-2, -1)) / math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9) # 将mask中为0的位置替换为极小的值
p_atten = F.softmax(scores, dim=-1)
if dropout is not None:
p_atten = dropout(p_atten)
return torch.matmul(p_atten, value), p_atten3.3.4 自注意力的效果
对于序列 I have a dream ,可以通过self-attention获得就会形成一张 4 × 4 的注意力机制的图,每一个单词就对应每一个单词有一个权重。

在编码器里是 self-attention,在解码器里是 masked self-attention,就是沿着对角线把灰色的区域用 0 覆盖掉,不给模型看到未来的信息。
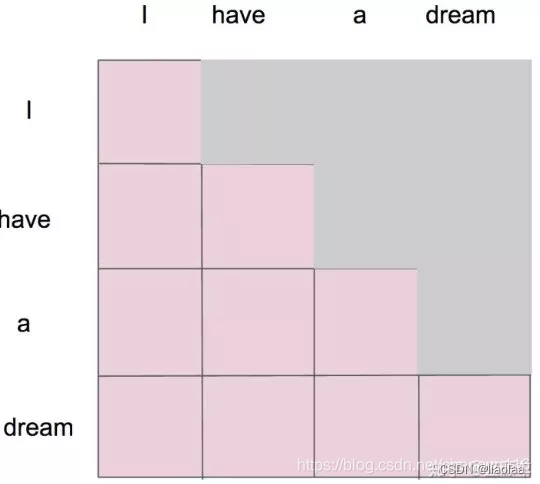
就是说,在第一个词 I 的时候,只能和 I 自己有 attention,第二个词 have 的时候,只有 I 、have 两个词的 attention,以此类推如下图。

3.3.5 什么是多头注意力机制(Multi-Head Attention)

从多头注意力机制的结构图中,多头就是使用多个Scale Dot-Product Attention,但是输入部分使用完全相同的多组线性层对Q,K,V做变换即可,每个Scale Dot-Product Attention开始从词义层面分割输出的张量,每个Scale Dot-Product Attention都会获得各自的Q,K,V进行自注意力的计算,最后取最后一维的词嵌入向量(即句子中的每个词的表示都只截取一部分)做拼接,这就是多头。

3.3.6 多头注意力机制的作用
一个词经过embedding之后获取一个高维稠密向量的表示,我们对这个稠密向量截取出来的信息都是不同的,比如embedding_dim=512,分h份截取出来的信息都是不一样的(注:我们的embedding_dim必须得被头数h整除,也就是必须h等分)。让每个注意力机制去优化每个词汇的不同特征的部分,防止偏差,让词语拥有来自更多元的表达。
3.3.7 多头注意力机制的实现
def clones(module, N):
"""
在多头注意力机制中需要使用多个完全相同的线性层
将它们初始化到一个网络层列表对象中
:param module:
:param N: 将module复制的个数
:return:
"""
return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
class MultiHeadedAttention(nn.Module):
def __init__(self, head, embedding_dim, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
# embedding_dim一定要被head整除
assert embedding_dim % head == 0
# 每个head截取的embedding_dim维度
self.d_k = embedding_dim // head
self.head = head
self.embedding_dim = embedding_dim
# 获得4个线性层,QKV各自需要使用一个,最后concat的之后需要使用一个
self.linears = clones(module=nn.Linear(embedding_dim, embedding_dim), N=4)
# 初始化注意力矩阵
self.atten = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
mask = mask.unsqueeze(1) # 需要扩充维度给head,表示第几个head
batch_size = query.size(0)
query, key, value = [model(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2)
for model, x in zip(self.linears, (query, key, value))]
# [batch_size, head, seq_len, d_k]
# 每个head的输出传入到注意力层
x, self.atten = attention(query, key, value, mask, self.dropout)
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.head * self.d_k)
return self.linears[-1](x)这里我们做了一个transpose轴交换,因为我们需要注意力关注的是seq和embedding之间的信息,所以我们把seq_len这维和head这维交换,即[batch_size, seq_len, head, d_k] -> [batch_size, head, seq_len, d_k] 。
3.4 前馈全连接层、规范化层和子层连接结构
3.4.1 什么是基于位置的前馈网络(Position-wise Feed-Forward Networks)
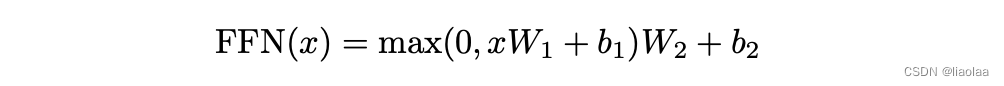
在编码器的注意力子层之后有一个前馈全连接层。我们的编码器和解码器中的每个层都包含一个全连接的前馈网络,该前馈网络单独且相同地应用于每个位置。它由两个线性变换组成,之间有一个 ReLU 激活。考虑到单纯一个注意力层可能泛化能力不够,所以增加了这一层。
3.4.2 什么是规范化层(Norm)
在所有的深层网络中都会有这样的层,随着网络层数的增加,通过多层的计算之后参数会慢慢变得很大或者很小(超出LongTensor表示范围,梯度爆炸或着梯度消失),会让模型参数学习过程出现异常,模型收敛可能很慢或者出错,所以我们在堆叠了一定网络层数之后会接上一个规范化层,把特征数值拉回合理的区间范围。在这里我们对词嵌入的维度做规范化。
3.4.3 子层连接结构-残差连接
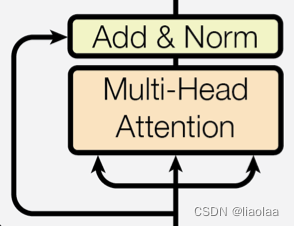
如上图,在编码器和解码器中每个子层之间都采用残差连接(跳接)的结构,有以下几点作用:
1. 信息传递:残差连接允许特征信息直接传导至下一层,有助于信息的流动和网络的训练;
2. 梯度回传:通过残差连接,梯度可以快速地回传;
3. 梯度保持:随着网络层数堆叠,神经元的相关性和梯度的空间结构会逐渐减弱,通过残差连接在一定程度上解决了梯度消失问题,并保留了梯度的空间结构。
Reference
https://arxiv.org/pdf/1706.03762.pdf
Attention Is All You Need-CSDN博客
深入探讨:残差网络解决了什么,为什么有效?