0、引入
假设给定一个长度为 1001 的数组,即下标 0 到 1000。
现在需要完成 3 个功能:
add(1, 200, 6); //给下标 1 到 200 的每个数都加 6;
update(7, 375, 4); //下标 7 到 375 的数全部修改为 4
query(3, 999); //下标 3 到 999 所有数的累加和
如果暴力解,则上述的每个功能的时间复杂度都为 O ( N ) O(N) O(N);而如果是使用线段树,则可以做到时间复杂度 O ( l o g N ) O(logN) O(logN)。
1、简介
为了简单起见,涉及到线段树的数组下标从 1 开始。
线段树是一种支持范围整体修改和范围整体查询的数据结构。
首先,希望将一个数组分成树状
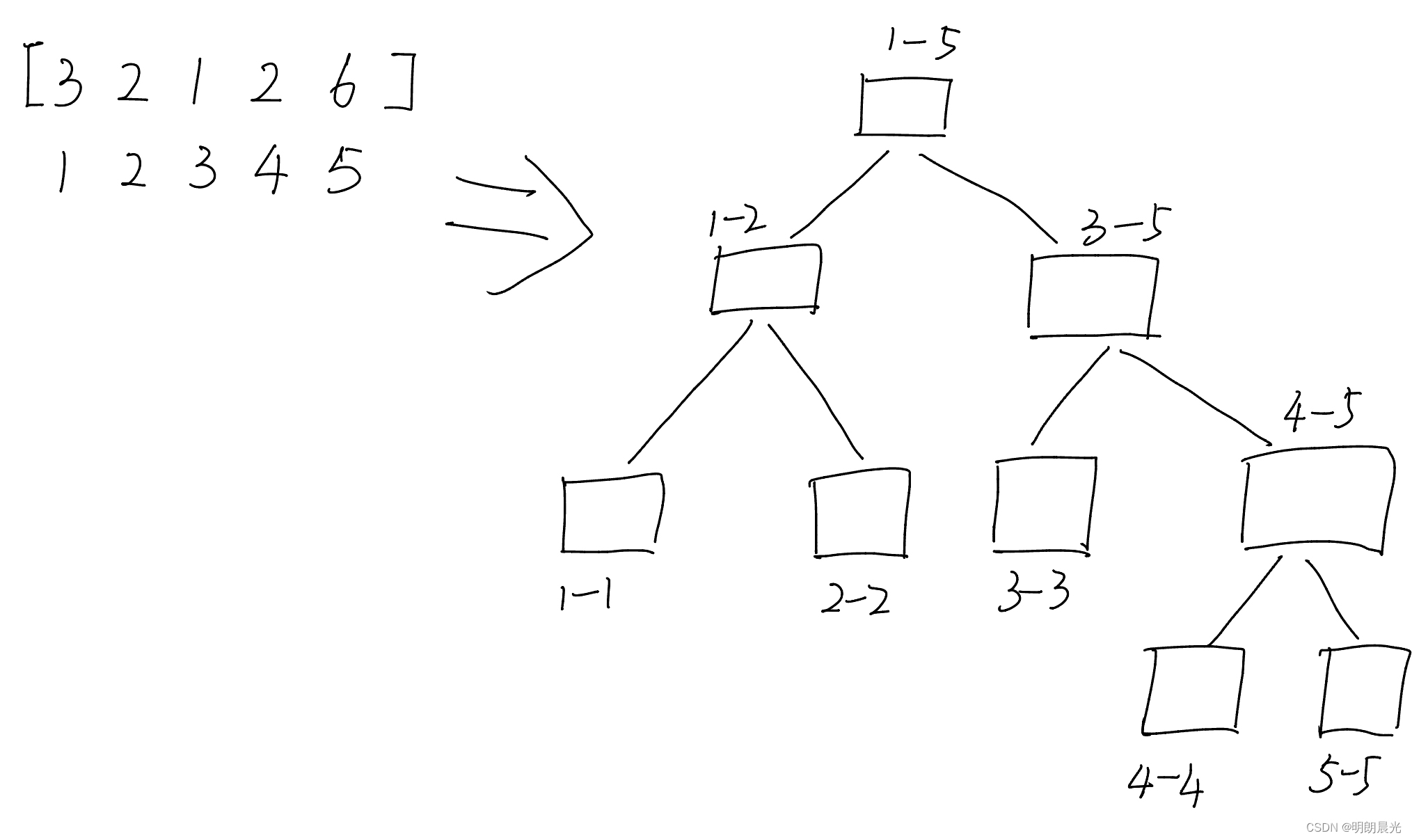
怎么做到呢?申请一个数组,只要满足下标
i
i
i 的父节点是
i
/
2
i/2
i/2 ,左孩子为
i
∗
2
i * 2
i∗2,右孩子为
i
∗
2
+
1
i * 2 + 1
i∗2+1 就能转换为一个树状。
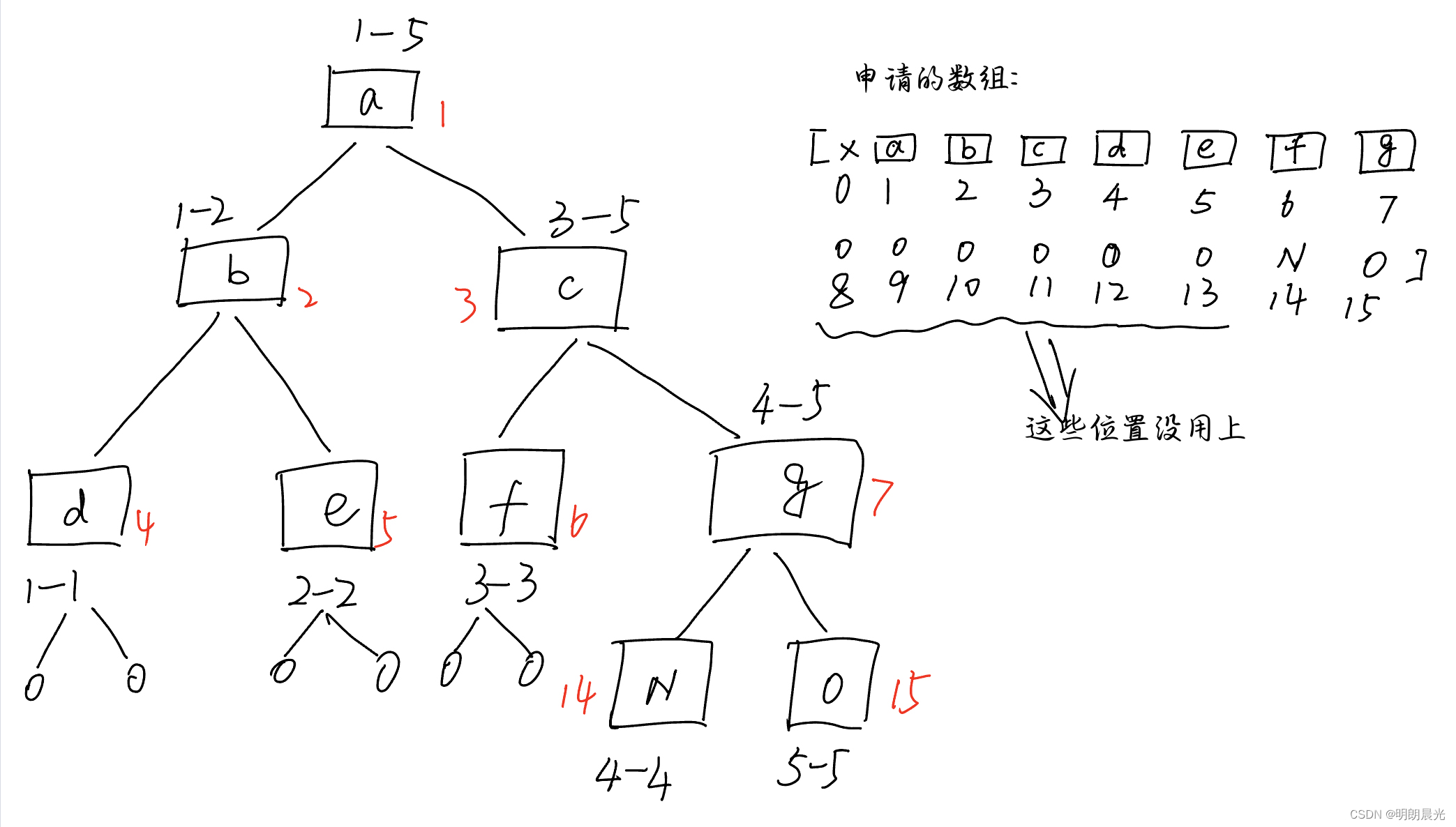
那么 申请的数组到底要准备多长呢? 如果原数组长度为
N
N
N,则准备
4
N
4N
4N 长度是够用的,包括一些用不上的位置。
这个结论怎么来的呢?
首先,当数组长度为 2 x 2^x 2x 次方时最省空间,因为没有废的空间。例长度为 4 时,申请 7 长度的的数组(0位置不用,下标1到7)即可, 就算包含弃而不用的 0 位置,也只需要 8 长度的空间。
当数组长度为 2 x + 1 2^x+1 2x+1 时,最费空间,但是也不会超过 4 N 4N 4N 长度。
2、懒更新:add
例如要给 3 ~ 874 下标范围的每个值都 +5,懒更新就是当树状数组中的某个范围包含在 3 ~ 874 时,就不再往下下发任务,而是就地处理。即只要树状中包含的数组范围没有完全包含在3 ~ 874中,就下发任务。
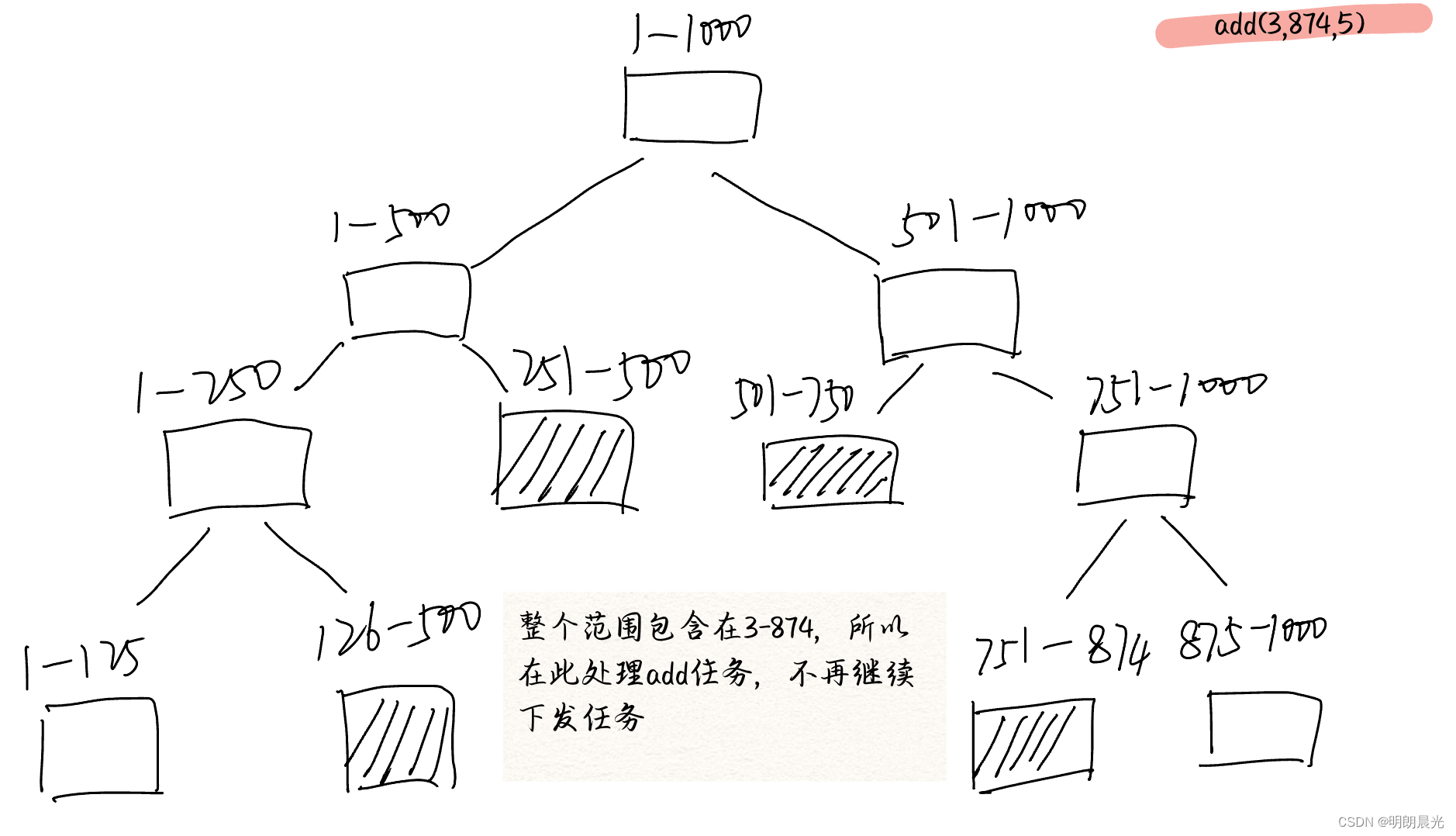
可以认为当一个任务到来时,卡着左边界和右边界各下放一次,中间该懒的就懒了(不往下发),时间复杂度
O
(
l
o
g
n
)
O(logn)
O(logn) 级别,非常快。
具体来说,就是一开始准备一个累加和数组(即
4
N
4N
4N长度)和一个懒更新数组,初始时:
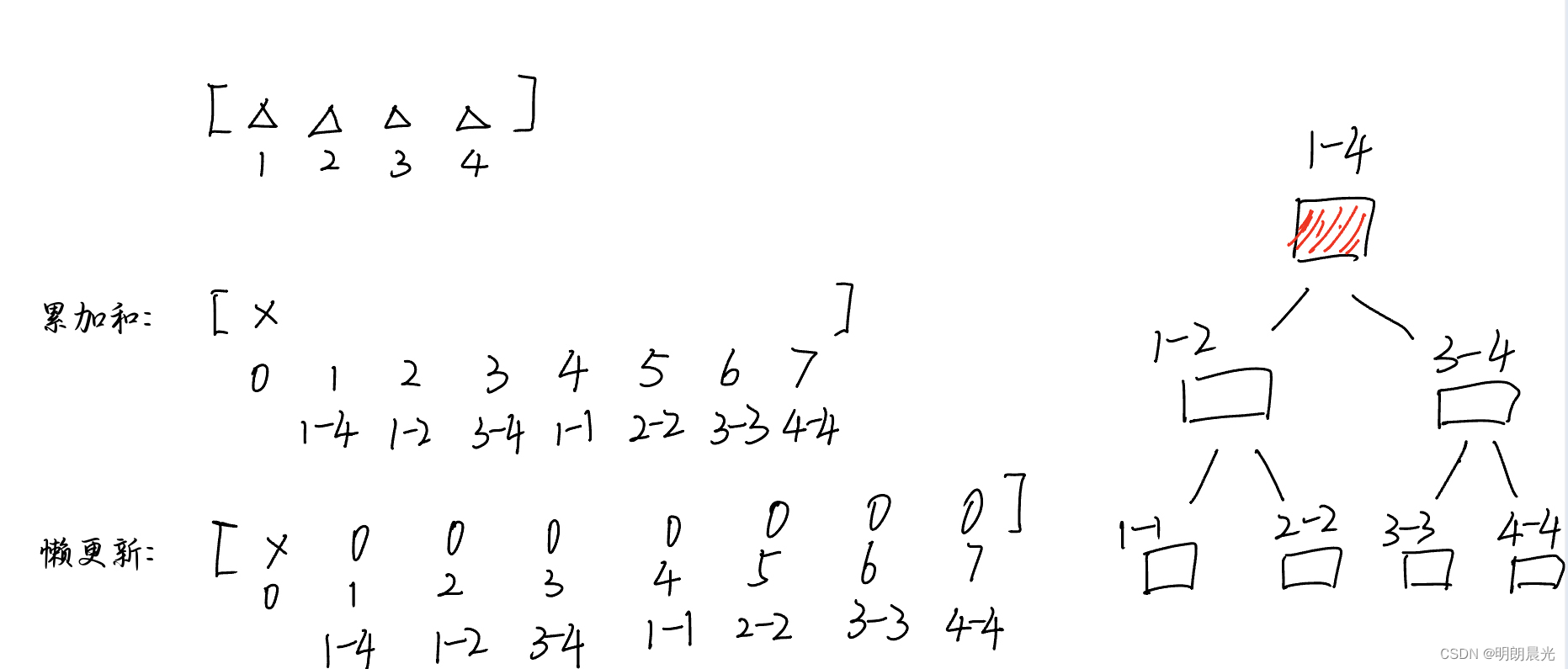
如果来了一个任务 add(1,4,3),即1~4下标范围的每个数都+3,对应到树状中,树根的范围已经完全包含在这个任务要求的范围中了,于是不再下发任务,而是就地处理。于是,懒更新数组更新为:
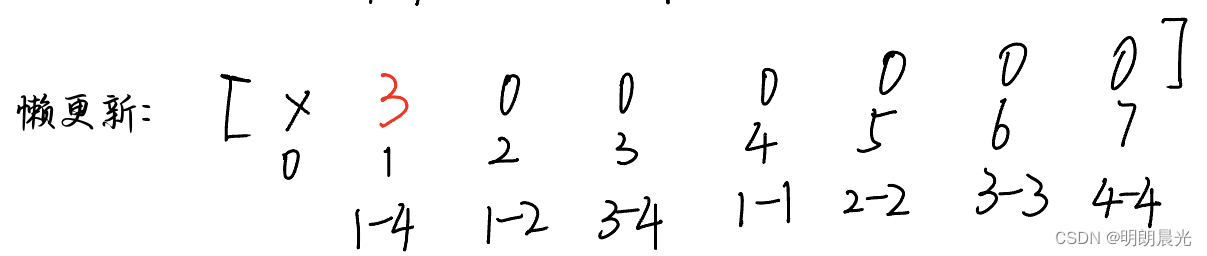
如果接着又来了一个任务 add(1,2,4)。首先,先看是否有懒信息,当前的情况是有,于是将该信息下发一层(下发到1-2 和 3-4),然后清空本层的懒信息:

然后执行任务 add(1,2,4),这个任务只需要分给 1-2,于是1-2 这个格子就得到了每个数+4的任务,先检查之前1-2 是否有懒信息,发现有,于是将当前的懒信息往下下发一层(1-1 和 2-2),将自己清空,发现任务1-2 包含了当前的1-2,于是拦住这个任务,1-2 的懒信息更新为4:
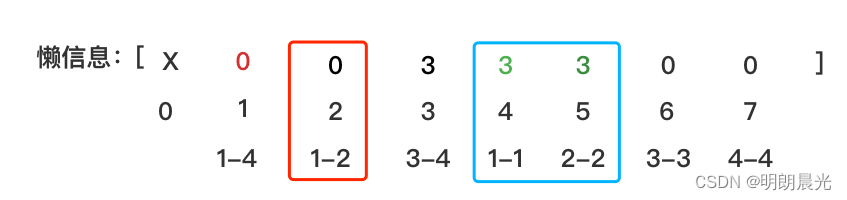
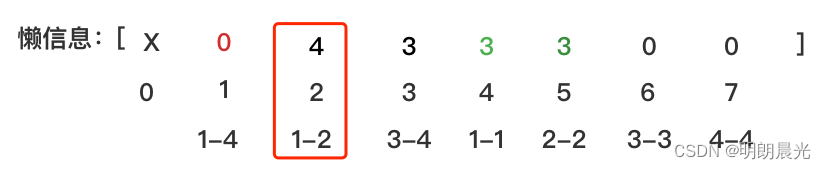
也就是如果当前层有懒信息,需要先将任务往下发一层然后再执行新任务。
3、懒更新:update
change 数组和 lazy 数组、sum 数组一样,都是原数组长度的 4 倍,只是用于记录原数组的不同信息。
为什么需要一个布尔类型的数组 update 呢?
例如原数组下标为1 ~ 500:
sum[1] = 100 万表示1 ~ 500 的累加和为 100万,而sum[1] = 0表示累加和为0,没有歧义;add[1] = 7表示 1 ~ 500 每个数加7,而add[1] = 0无论是每个数都加0 还是 表示没有懒信息 都是可以的;change[1] = 7表示1 ~ 500 的每个数都修改为7;但是change[1] = 0就有歧义,不知道是1 ~ 500 每个数都变成 0 还是 1 ~ 500 的每个数没有update信息,造成了歧义。
所以再增加一个布尔类型的 update 数组,如果 update[1] = 1, change[1] = 0 就表示 1 ~ 500 的每个数变成0;而update = 0, change[1] = 0 表示没有关于 update 的懒信息,原数组该什么样就什么样。
4、懒更新:query
当需要查询区间的累加和时,要先将区间的其他任务(更新、累加)进行下发,然后执行查询任务。
5、解决的问题
线段树是用于解决区间增加、区间更新和区间查询的问题。
6、线段树代码实现
public class SegmentTree {
public static class SegmentTree {
private int MAXN;
private int[] arr; //缓存数组,原序列的信息从0开始,但在arr里是从1开始的,0位置不用
private int[] sum; //模拟线段树维护区间和,原数组arr长度扩4倍
private int[] lazy; //为累加和懒惰标记,原数组arr长度扩4倍
private int[] change; //范围上所有的值被更新成的值
private boolean[] update; //update信息的慵懒标记,是否有修改信息
public SegmentTree(int[] origin) {
MAXN = origin.length + 1;
arr = new int[MAXN]; // arr[0]不用,从1开始使用
for (int i = 1; i < MAXN; i++) {
arr[i] = origin[i - 1];
}
sum = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围的累加和信息
lazy = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围沒有往下傳遞的纍加任務
change = new int[MAXN << 2]; // 用来支持脑补概念中,某一个范围有没有更新操作的任务
update = new boolean[MAXN << 2]; // 用来支持脑补概念中,某一个范围更新任务,更新成了什么
}
private void pushUp(int rt) { //树状中根的累加和 = 左孩子的累加和 + 右孩子的累加和
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; //sum[i] = sum[2*i] + sum[2*i+1]
}
// 之前的,所有懒增加,和懒更新,从父范围,发给左右两个子范围
// 分发策略是什么
// rt表示父节点的下标,ln表示左子树元素结点个数,rn表示右子树结点个数
private void pushDown(int rt, int ln, int rn) {
//先检查“更新”信息,再检查“累加”信息
//之所以这样,是因为在update()函数操作的时候会将lazy信息清空
//如果既有update信息又有lazy信息,则说明最近一次更新到目前为止又攒了几个累加信息
//所以在分发任务的时候要先检查“更新”,再检查“累加”,因为两者同时存在时,更新是早的,累加是后攒起来的
if (update[rt]) { //如果父节点有“更新”信息,则下发一级
//左右孩子都有更新信息
update[rt << 1] = true;
update[rt << 1 | 1] = true;
//左右孩子都改成父节点的change信息
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
//左右孩子的累加和(lazy)信息都清空,被update信息覆盖掉
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
//左右孩子的累加和重新计算
sum[rt << 1] = change[rt] * ln;
sum[rt << 1 | 1] = change[rt] * rn;
//父节点的“更新”信息清空
update[rt] = false;
}
if (lazy[rt] != 0) { //有懒信息,向下分发一级:更新左右孩子的累加和信息和和懒信息
lazy[rt << 1] += lazy[rt]; //左孩子的懒信息加上父节点的懒信息
sum[rt << 1] += lazy[rt] * ln; //左孩子的累加和更新加上左边节点个数 * 懒信息
lazy[rt << 1 | 1] += lazy[rt]; //右孩子的懒信息加上父节点的懒信息
sum[rt << 1 | 1] += lazy[rt] * rn; //右孩子的累加和更新
lazy[rt] = 0; //孩子承接了懒任务,所以父节点的懒信息清零
}
}
// 该函数就是将原数组建立成一个树状结构,最大范围一定在 1 这个下标上
// 在初始化阶段,先把sum数组,填好
// 在arr[l~r]范围上,去build,1~N,
// rt : 这个范围在sum中的下标
public void build(int l, int r, int rt) { //l~r这个范围在sum数组中对应的下标为rt
if (l == r) { //叶节点,只有一个数,将原数组中的l范围的值填到sum[rt]即可
sum[rt] = arr[l];
return;
}
int mid = (l + r) >> 1; //求出中点
build(l, mid, rt << 1); //左孩子
build(mid + 1, r, rt << 1 | 1); //右孩子
pushUp(rt); //计算出左孩子和右孩子后,将左右孩子相加得到根节点的值
}
//任务:将L到R范围上的数都修改为C
//目前到了rt这个下标的节点,它代表的是l到r区间
public void update(int L, int R, int C, int l, int r, int rt) {
//任务把此时的范围全部包括了
if (L <= l && r <= R) {
update[rt] = true; //设置“更新”操作的懒信息
change[rt] = C; //“更新”操作的懒信息
sum[rt] = C * (r - l + 1); //直接设置累加和
lazy[rt] = 0; //因为已经进行了“更新”操作,所以之前累加和的懒信息全部清空
return;
}
// 当前任务躲不掉,无法懒更新,要往下发
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid); //检查是否有老任务要先下发
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
// L到R范围上的每个数都加C (即任务),是固定的
// 当前来到的格子是rt,表示的范围是l到r
public void add(int L, int R, int C, int l, int r, int rt) {
// 任务如果把此时的范围全包了!
//如任务为[3,874]范围的每个数都加5,而当前来到的是树状的3位置的[251,500]区间
//因为[251,500] 包含在[3,874],则懒更新,即直接在这里处理任务,而不是下发任务
if (L <= l && r <= R) {
sum[rt] += C * (r - l + 1); //l到r范围共r-l+1个数,则累加和变大 C*(r-l+1)
lazy[rt] += C; //懒更新信息
return;
}
// 任务没有把你全包!
// l r mid = (l+r)/2
int mid = (l + r) >> 1;
//先处理老任务
pushDown(rt, mid - l + 1, r - mid); //如果有懒信息先下发一级再处理当前的任务
//然后处理新任务
if (L <= mid) { //任务需要发给左边
add(L, R, C, l, mid, rt << 1);
}
if (R > mid) { //任务需要发给右边
add(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt); //调整自己的累加和
}
// 任务:查询L到R范围上的累加和
// 目前到了下标为rt的节点,代表的区间是l到r
public long query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
//将之前缓存的任务先下发在处理查询
pushDown(rt, mid - l + 1, r - mid);
long ans = 0;
if (L <= mid) { //任务需要分给左边,左边的查询结果
ans += query(L, R, l, mid, rt << 1);
}
if (R > mid) { //任务需要分给右边,右边的查询结果
ans += query(L, R, mid + 1, r, rt << 1 | 1);
}
return ans;
}
}
//纯暴力
public static class Right {
public int[] arr;
public Right(int[] origin) {
arr = new int[origin.length + 1];
for (int i = 0; i < origin.length; i++) {
arr[i + 1] = origin[i];
}
}
public void update(int L, int R, int C) {
for (int i = L; i <= R; i++) {
arr[i] = C;
}
}
public void add(int L, int R, int C) {
for (int i = L; i <= R; i++) {
arr[i] += C;
}
}
public long query(int L, int R) {
long ans = 0;
for (int i = L; i <= R; i++) {
ans += arr[i];
}
return ans;
}
}
public static int[] genarateRandomArray(int len, int max) {
int size = (int) (Math.random() * len) + 1;
int[] origin = new int[size];
for (int i = 0; i < size; i++) {
origin[i] = (int) (Math.random() * max) - (int) (Math.random() * max);
}
return origin;
}
public static boolean test() {
int len = 100;
int max = 1000;
int testTimes = 5000;
int addOrUpdateTimes = 1000;
int queryTimes = 500;
for (int i = 0; i < testTimes; i++) {
int[] origin = genarateRandomArray(len, max);
SegmentTree seg = new SegmentTree(origin);
int S = 1;
int N = origin.length;
int root = 1;
seg.build(S, N, root);
Right rig = new Right(origin);
for (int j = 0; j < addOrUpdateTimes; j++) {
int num1 = (int) (Math.random() * N) + 1;
int num2 = (int) (Math.random() * N) + 1;
int L = Math.min(num1, num2);
int R = Math.max(num1, num2);
int C = (int) (Math.random() * max) - (int) (Math.random() * max);
if (Math.random() < 0.5) { //0.5的概率执行add
seg.add(L, R, C, S, N, root);
rig.add(L, R, C);
} else { //0.5的概率执行update
seg.update(L, R, C, S, N, root);
rig.update(L, R, C);
}
}
for (int k = 0; k < queryTimes; k++) {
int num1 = (int) (Math.random() * N) + 1;
int num2 = (int) (Math.random() * N) + 1;
int L = Math.min(num1, num2);
int R = Math.max(num1, num2);
long ans1 = seg.query(L, R, S, N, root);
long ans2 = rig.query(L, R);
if (ans1 != ans2) {
return false;
}
}
}
return true;
}
public static void main(String[] args) {
int[] origin = { 2, 1, 1, 2, 3, 4, 5 };
SegmentTree seg = new SegmentTree(origin);
int S = 1; // 整个区间的开始位置,规定从1开始,不从0开始 -> 固定
int N = origin.length; // 整个区间的结束位置,规定能到N,不是N-1 -> 固定
int root = 1; // 整棵树的头节点位置,规定是1,不是0 -> 固定
int L = 2; // 操作区间的开始位置 -> 可变
int R = 5; // 操作区间的结束位置 -> 可变
int C = 4; // 要加的数字或者要更新的数字 -> 可变
// 区间生成,必须在[S,N]整个范围上build
seg.build(S, N, root);
// 区间修改,可以改变L、R和C的值,其他值不可改变
seg.add(L, R, C, S, N, root);
// 区间更新,可以改变L、R和C的值,其他值不可改变
seg.update(L, R, C, S, N, root);
// 区间查询,可以改变L和R的值,其他值不可改变
long sum = seg.query(L, R, S, N, root);
System.out.println(sum);
System.out.println("对数器测试开始...");
System.out.println("测试结果 : " + (test() ? "通过" : "未通过"));
}
}