U参考来源
U
这里移植到windows 上 ,使用 devc++ 开发。
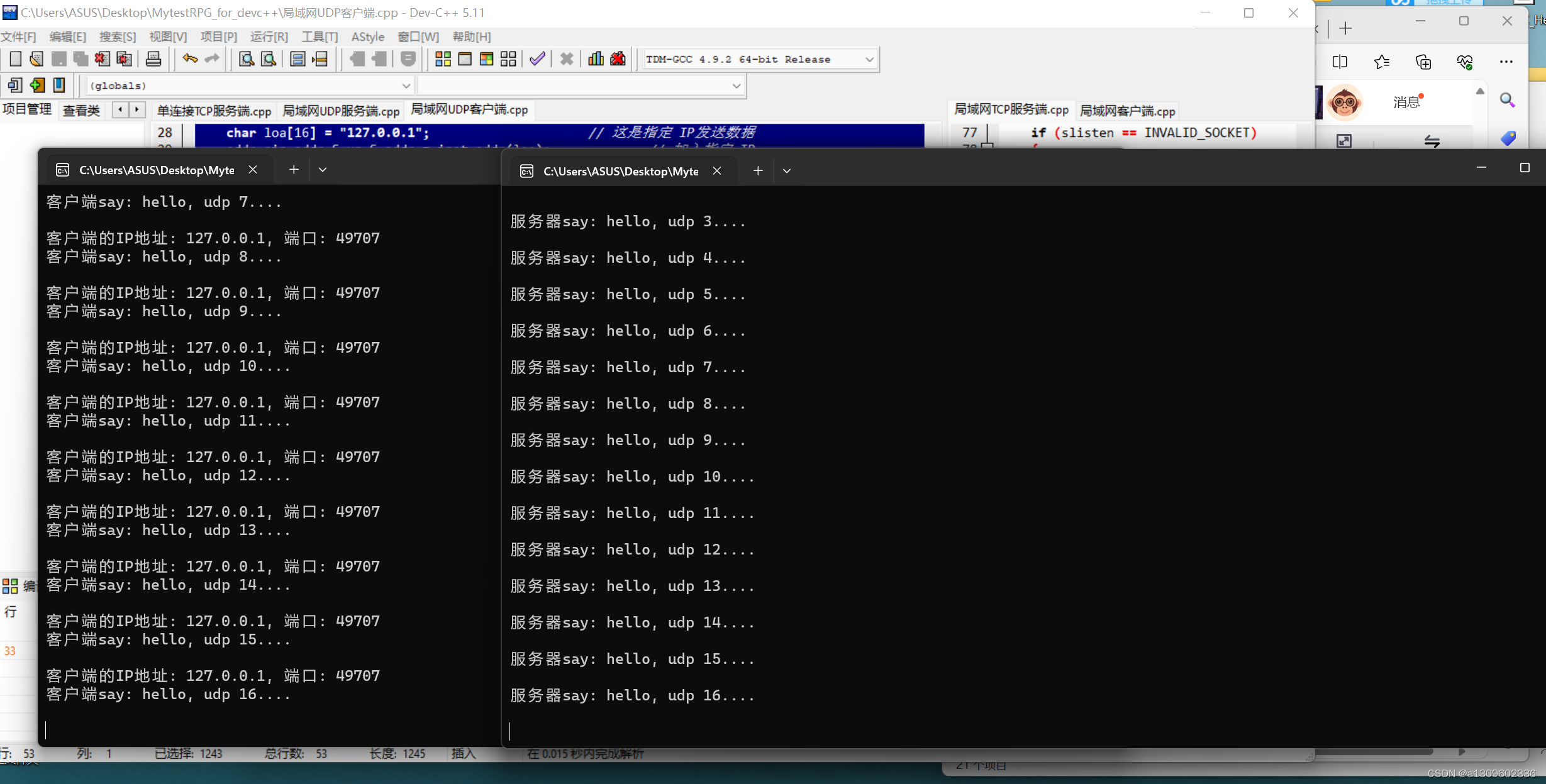
服务端代码
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include <winsock2.h>
int main()
{
WORD sockVersion = MAKEWORD(2, 2);
WSADATA data;
if (WSAStartup(sockVersion, &data) != 0)
{
return 0;
}
// 1. 创建通信的套接字
SOCKET fd = socket(AF_INET, SOCK_DGRAM, IPPROTO_UDP);
if (fd == INVALID_SOCKET)
{
printf("无效的 socket !");
return 0;
}
// 2. 通信的套接字和本地的IP与端口绑定
struct sockaddr_in addr;
addr.sin_family = AF_INET;
addr.sin_port = htons(9999); // 大端
addr.sin_addr.s_addr = htonl(INADDR_ANY); // 0.0.0.0
int ret = bind(fd, (struct sockaddr*)&addr, sizeof(addr));
if(ret == -1)
{
perror("bind");
exit(0);
}
char buf[1024];
struct sockaddr_in cliaddr;
int len = sizeof(cliaddr);
// 3. 通信
while(1)
{
// 接收数据
memset(buf, 0, sizeof(buf));
int rlen = recvfrom(fd, buf, sizeof(buf), 0, (struct sockaddr*)&cliaddr, &len);
printf("客户端的IP地址: %s, 端口: %d\n",
inet_ntoa(cliaddr.sin_addr),
ntohs(cliaddr.sin_port));
printf("客户端say: %s\n", buf);
// 回复数据
// 数据回复给了发送数据的客户端
sendto(fd, buf, rlen, 0, (struct sockaddr*)&cliaddr, sizeof(cliaddr));
}
close(fd);
return 0;
}客户端代码
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include <winsock2.h>
int main()
{
WORD sockVersion = MAKEWORD(2, 2);
WSADATA data;
if (WSAStartup(sockVersion, &data) != 0)
{
return 0;
}
// 1. 创建通信的套接字
SOCKET fd = socket(AF_INET, SOCK_DGRAM, IPPROTO_UDP);
if (fd == INVALID_SOCKET)
{
printf("无效的 socket !");
return 0;
}
// 2. 通信的套接字和本地的IP与端口绑定
struct sockaddr_in addr;
addr.sin_family = AF_INET;
addr.sin_port = htons(9999); // 大端
// addr.sin_addr.s_addr = htonl(INADDR_BROADCAST); // 255.255.255.255 广播
char loa[16] = "127.0.0.1"; // 这是指定 IP发送数据
addr.sin_addr.S_un.S_addr = inet_addr(loa); // 加入指定 IP
char buf[1024];
char ipbuf[64];
int num = 0;
// 2. 通信
while(1)
{
sprintf(buf, "hello, udp %d....\n", num++);
// 发送数据, 数据发送给了服务器
sendto(fd, buf, strlen(buf)+1, 0, (struct sockaddr*)&addr, sizeof(addr));
// 接收数据
memset(buf, 0, sizeof(buf));
recvfrom(fd, buf, sizeof(buf), 0, NULL, NULL);
printf("服务器say: %s\n", buf);
sleep(1);
}
close(fd);
return 0;
}