🌞欢迎来到PyTorch的世界
🌈博客主页:卿云阁💌欢迎关注🎉点赞👍收藏⭐️留言📝
🌟本文由卿云阁原创!
📆首发时间:🌹2024年2月16日🌹
✉️希望可以和大家一起完成进阶之路!
🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢!
目录
回归问题
建立数据集
建立神经网络
训练网络
可视化训练过程
分类问题
建立数据集
建立神经网络
训练网络
可视化训练过程
神经网络的快速搭建
保存和提取
搭建网络
两种途径来保存
提取网络
只提取网络参数
显示结果
输入端优化:梯度下降的三种方式
BGD梯度下降算法
SGD随机梯度下降法
小批量梯度下降算法
训练过程的优化-Optimizer 优化器
建立数据集
每个优化器优化一个神经网络
优化器 Optimizer
训练
回归问题
建立数据集
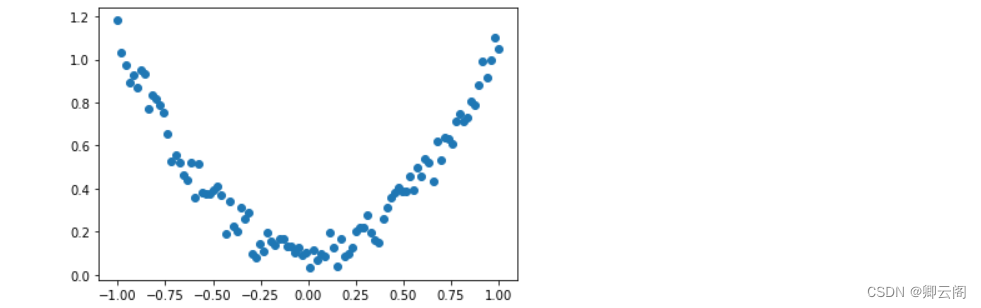
我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数:
y = a * x^2 + b, 我们给y数据加上一点噪声来更加真实的展示它.import torch import matplotlib.pyplot as plt x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1) y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1) # 画图 plt.scatter(x.data.numpy(), y.data.numpy()) plt.show()
建立神经网络
建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(
__init__()), 然后再一层层搭建(forward(x))层于层的关系链接.import torch import torch.nn.functional as F # 激励函数都在这 class Net(torch.nn.Module): # 继承 torch 的 Module def __init__(self, n_feature, n_hidden, n_output): super(Net, self).__init__() # 继承 __init__ 功能 # 定义每层用什么样的形式 self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出 self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出 def forward(self, x): # 这同时也是 Module 中的 forward 功能 # 正向传播输入值, 神经网络分析出输出值 x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值) x = self.predict(x) # 输出值 return x net = Net(n_feature=1, n_hidden=10, n_output=1) print(net) # net 的结构 Net( (hidden): Linear(in_features=1, out_features=10, bias=True) (predict): Linear(in_features=10, out_features=1, bias=True) )训练网络
训练的步骤如下:
# optimizer 是训练的工具 optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 传入 net 的所有参数, 学习率 loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差) for t in range(100): prediction = net(x) # 喂给 net 训练数据 x, 输出预测值 loss = loss_func(prediction, y) # 计算两者的误差 optimizer.zero_grad() # 清空上一步的残余更新参数值 loss.backward() # 误差反向传播, 计算参数更新值 optimizer.step() # 将参数更新值施加到 net 的 parameters 上可视化训练过程
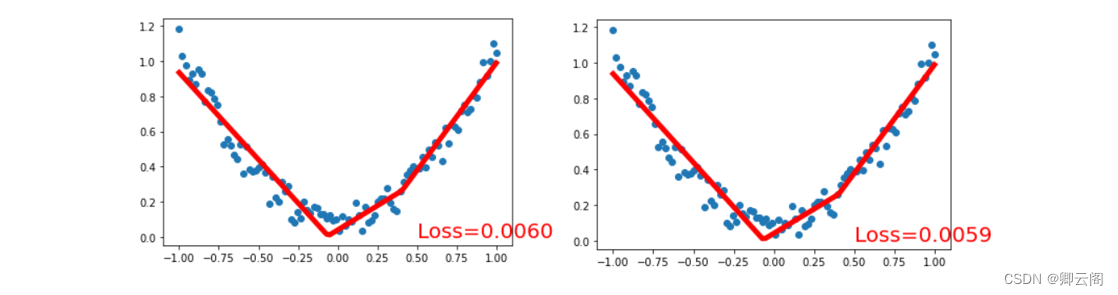
为了可视化整个训练的过程, 更好的理解是如何训练, 我们如下操作:
import matplotlib.pyplot as plt plt.ion() # 画图 plt.show() for t in range(200): prediction = net(x) # 喂给 net 训练数据 x, 输出预测值 loss = loss_func(prediction, y) # 计算两者的误差 optimizer.zero_grad() # 清空上一步的残余更新参数值 loss.backward() optimizer.step() # 接着上面来 if t % 5 == 0: # plot and show learning process plt.cla() plt.scatter(x.data.numpy(), y.data.numpy()) plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5) plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'}) plt.pause(0.1)
分类问题
建立数据集
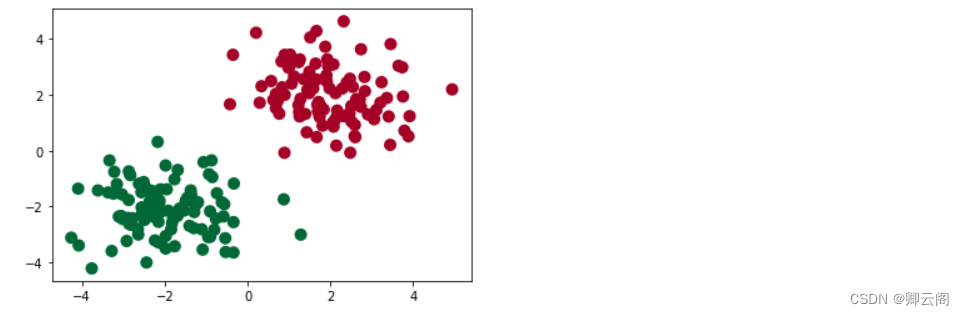
我们创建一些假数据来模拟真实的情况.
import torch import matplotlib.pyplot as plt # 假数据 n_data = torch.ones(100, 2) # 数据的基本形态 x0 = torch.normal(2*n_data, 1) # 类型0 x data (tensor), shape=(100, 2) y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100, ) x1 = torch.normal(-2*n_data, 1) # 类型1 x data (tensor), shape=(100, 1) y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100, ) # 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据) x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # FloatTensor = 32-bit floating y = torch.cat((y0, y1), ).type(torch.LongTensor) # LongTensor = 64-bit integer plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn') plt.show()
建立神经网络
import torch import torch.nn.functional as F # 激励函数都在这 class Net(torch.nn.Module): # 继承 torch 的 Module def __init__(self, n_feature, n_hidden, n_output): super(Net, self).__init__() # 继承 __init__ 功能 self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出 self.out = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出 def forward(self, x): # 正向传播输入值, 神经网络分析出输出值 x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值) x = self.out(x) # 输出值, 但是这个不是预测值, 预测值还需要再另外计算 return x net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output print(net) # net 的结构 """ Net ( (hidden): Linear (2 -> 10) (out): Linear (10 -> 2) ) """训练网络
# optimizer 是训练的工具 optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # 传入 net 的所有参数, 学习率 # 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,) # 但是预测值是2D tensor (batch, n_classes) loss_func = torch.nn.CrossEntropyLoss() for t in range(100): out = net(x) # 喂给 net 训练数据 x, 输出分析值 loss = loss_func(out, y) # 计算两者的误差 optimizer.zero_grad() # 清空上一步的残余更新参数值 loss.backward() # 误差反向传播, 计算参数更新值 optimizer.step() # 将参数更新值施加到 net 的 parameters 上可视化训练过程
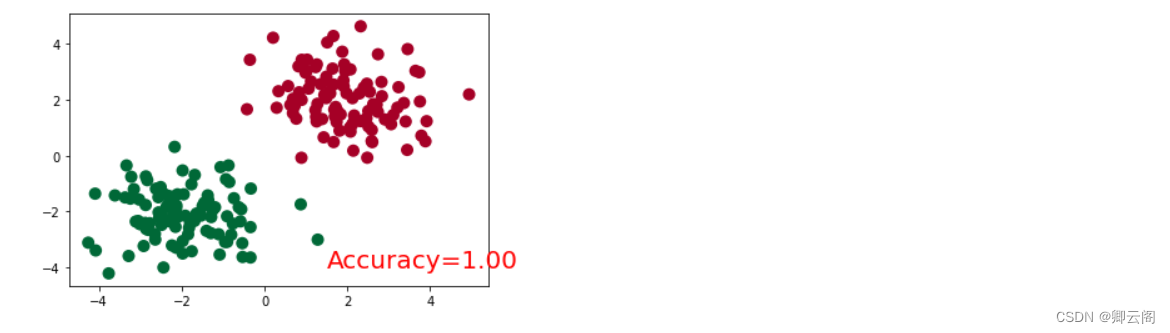
import matplotlib.pyplot as plt plt.ion() # 画图 plt.show() for t in range(100): out = net(x) # 喂给 net 训练数据 x, 输出分析值 loss = loss_func(out, y) # 计算两者的误差 optimizer.zero_grad() # 清空上一步的残余更新参数值 loss.backward() optimizer.step() # 接着上面来 if t % 2 == 0: plt.cla() # 过了一道 softmax 的激励函数后的最大概率才是预测值 prediction = torch.max(F.softmax(out), 1)[1] pred_y = prediction.data.numpy().squeeze() target_y = y.data.numpy() plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn') accuracy = sum(pred_y == target_y)/200. # 预测中有多少和真实值一样 plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'}) plt.pause(0.1) plt.ioff() # 停止画图 plt.show()
神经网络的快速搭建
class Net(torch.nn.Module): def __init__(self, n_feature, n_hidden, n_output): super(Net, self).__init__() self.hidden = torch.nn.Linear(n_feature, n_hidden) self.predict = torch.nn.Linear(n_hidden, n_output) def forward(self, x): x = F.relu(self.hidden(x)) x = self.predict(x) return x net1 = Net(1, 10, 1) # 这是我们用这种方式搭建的 net1net2 = torch.nn.Sequential( torch.nn.Linear(1, 10), torch.nn.ReLU(), torch.nn.Linear(10, 1) )print(net1) """ Net ( (hidden): Linear (1 -> 10) (predict): Linear (10 -> 1) ) """ print(net2) """ Sequential ( (0): Linear (1 -> 10) (1): ReLU () (2): Linear (10 -> 1) ) """
net2多显示了一些内容, 这是为什么呢? 原来他把激励函数也一同纳入进去了, 但是net1中, 激励函数实际上是在forward()功能中才被调用的. 这也就说明了, 相比net2,net1的好处就是, 你可以根据你的个人需要更加个性化你自己的前向传播过程, 比如(RNN).
保存和提取
搭建网络
torch.manual_seed(1) # reproducible # 假数据 x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1) y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1) def save(): # 建网络 net1 = torch.nn.Sequential( torch.nn.Linear(1, 10), torch.nn.ReLU(), torch.nn.Linear(10, 1) ) optimizer = torch.optim.SGD(net1.parameters(), lr=0.5) loss_func = torch.nn.MSELoss() # 训练 for t in range(100): prediction = net1(x) loss = loss_func(prediction, y) optimizer.zero_grad() loss.backward() optimizer.step()两种途径来保存
torch.save(net1, 'net.pkl') # 保存整个网络 torch.save(net1.state_dict(), 'net_params.pkl') # 只保存网络中的参数 (速度快, 占内存少)提取网络
这种方式将会提取整个神经网络, 网络大的时候可能会比较慢.
def restore_net(): # restore entire net1 to net2 net2 = torch.load('net.pkl') prediction = net2(x)只提取网络参数
这种方式将会提取所有的参数, 然后再放到你的新建网络中.
def restore_params(): # 新建 net3 net3 = torch.nn.Sequential( torch.nn.Linear(1, 10), torch.nn.ReLU(), torch.nn.Linear(10, 1) ) # 将保存的参数复制到 net3 net3.load_state_dict(torch.load('net_params.pkl')) prediction = net3(x)显示结果
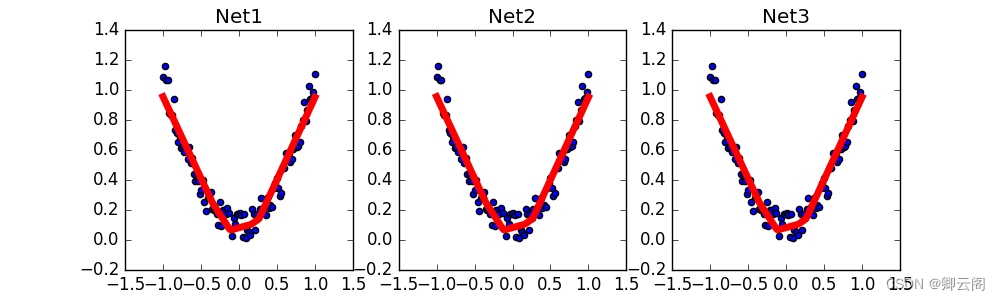
调用上面建立的几个功能, 然后出图.
#plot result plt.subplot(132) plt.title('Net2') plt.scatter(x.data.numpy(),y.data.numpy()) plt.plot(x.data.numpy(),prediction.data.numpy(),'r-',lw=5)
输入端优化:梯度下降的三种方式
形式 特点 Batch Gradient Descent 批量梯度下降算法 直接整个数据集来训练,若数据量大将面临内存不足,收敛速度慢问题直接整个数据集来训练,若数据量大将面临内存不足,收敛速度慢问题 Stochastic Gradient Descent 随机梯度下降算法(在线学习) 一个一个数据来训练,每训练一个就更新一次参数,收敛速度较快,但是可能高频的参数更新导致方差过大最终导致目标函数数值震荡 Mini-batch Gradient Descent 小批量梯度下降算法 综合BGD和SGD算法,每次取一小个batch数量的数据来计算,训练过程较稳定 BGD梯度下降算法
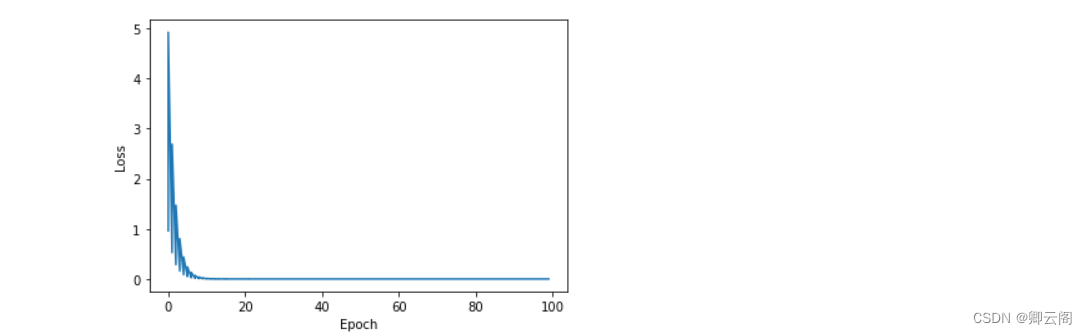
import numpy as np import matplotlib.pyplot as plt # Initialize parameters x_data = [1.0, 2.0, 3.0] y_data = [2.0, 4.0, 6.0] w = 1.0 # Define function def forward(x): return x * w # Define the loss function def cost(xs, ys): cost = 0 for x, y in zip(xs, ys): y_pred = forward(x) cost += (y_pred - y) ** 2 return cost / len(xs) # Gradient function def gradient(xs, ys): grad = 0 for x, y in zip(xs, ys): grad += 2 * x * (x * w - y) return grad / len(xs) cost_list = [] epoch_list = [] # Trainging for epoch in range(100): epoch_list.append(epoch) cost_val = cost(x_data, y_data) cost_list.append(cost_val) grad_val = gradient(x_data, y_data) w -= 0.1 * grad_val print('Epoch:', epoch, 'w=', w, 'loss=', cost_val) # Visualize the results plt.plot(epoch_list, cost_list) plt.ylabel('Loss') plt.xlabel('Epoch') plt.show()
可以很明显的看到,随着训练的进行,Loss是平滑的收敛于0。
SGD随机梯度下降法
SGD与BGD最大的不同在于每个epoch,SGD是一个一个数据来训练,BGD是所有数据一起训练 。
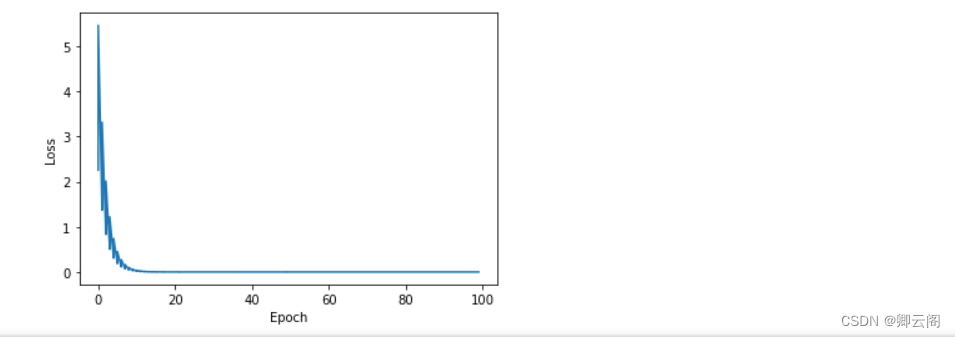
import numpy as np import matplotlib.pyplot as plt # Initialize parameters x_data = [1.0, 2.0, 3.0] y_data = [2.0, 4.0, 6.0] w = 1.0 # Define function def forward(x): return x * w # Define the loss function def loss(x, y): y_pred = forward(x) return (y_pred - y) ** 2 # Gradient function def gradient(x, y): return 2 * x * (x * w - y) loss_list = [] epoch_list = [] # Trainging for epoch in range(100): for x, y in zip(x_data, y_data): grad = gradient(x, y) w -= 0.01 * grad Loss = loss(x, y) loss_list.append(Loss) epoch_list.append(epoch) print('Epoch:', epoch, 'w=', w, 'loss=', Loss) # Visualize the results plt.plot(epoch_list, loss_list) plt.ylabel('Loss') plt.xlabel('Epoch') plt.show()
可以看到明显的看到,随着训练的进行,Loss上下浮动的收敛于0。
小批量梯度下降算法
import numpy as np import matplotlib.pyplot as plt # Initialize parameters x_data = np.array([1.0, 2.0, 3.0]) y_data = np.array([2.0, 4.0, 6.0]) w = 1.0 # Define function def forward(x): return x * w # Define the loss function def loss(x, y): y_pred = forward(x) return (y_pred - y) ** 2 # Gradient function def gradient(x, y): return 2 * x * (x * w - y) # Mini-batch gradient descent parameters batch_size = 2 learning_rate = 0.01 epochs = 100 loss_list = [] epoch_list = [] # Training for epoch in range(epochs): for i in range(0, len(x_data), batch_size): x_batch = x_data[i:i+batch_size] y_batch = y_data[i:i+batch_size] grad = gradient(x_batch, y_batch).mean() w -= learning_rate * grad Loss = loss(x_batch, y_batch).mean() loss_list.append(Loss) epoch_list.append(epoch) print('Epoch:', epoch, 'w=', w, 'loss=', Loss) # Visualize the results plt.plot(epoch_list, loss_list) plt.ylabel('Loss') plt.xlabel('Epoch') plt.show()
可以看到明显的看到,随着训练的进行,Loss上下浮动的收敛于0。
训练过程的优化-Optimizer 优化器
越复杂的神经网络 , 越多的数据 , 我们需要在训练神经网络的过程上花费的时间也就越多. 原因很简单, 就是因为计算量太大了. 可是往往有时候为了解决复杂的问题, 复杂的结构和大数据又是不能避免的, 所以我们需要寻找一些方法, 让神经网络聪明起来, 快起来.这些基本都是在参数更新上不同。
- Stochastic Gradient Descent (SGD)
- Momentum 更新方法
- AdaGrad 更新方法
- RMSProp 更新方法
- Adam 更新方法
建立数据集
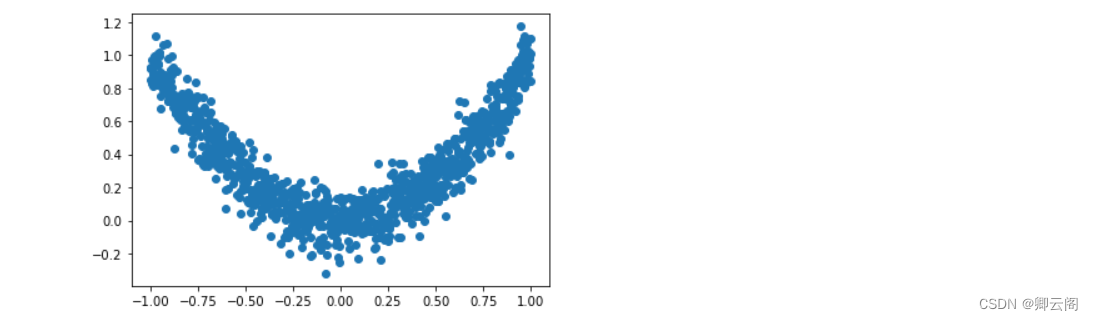
import torch import torch.utils.data as Data import torch.nn.functional as F import matplotlib.pyplot as plt torch.manual_seed(1) # reproducible LR = 0.01 BATCH_SIZE = 32 EPOCH = 12 # fake dataset x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1) y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size())) # plot dataset plt.scatter(x.numpy(), y.numpy()) plt.show() # 使用上节内容提到的 data loader torch_dataset = Data.TensorDataset(x, y) loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
每个优化器优化一个神经网络
为了对比每一种优化器, 我们给他们各自创建一个神经网络, 但这个神经网络都来自同一个
Net形式.# 默认的 network 形式 class Net(torch.nn.Module): def __init__(self): super(Net, self).__init__() self.hidden = torch.nn.Linear(1, 20) # hidden layer self.predict = torch.nn.Linear(20, 1) # output layer def forward(self, x): x = F.relu(self.hidden(x)) # activation function for hidden layer x = self.predict(x) # linear output return x # 为每个优化器创建一个 net net_SGD = Net() net_Momentum = Net() net_RMSprop = Net() net_Adam = Net() nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]优化器 Optimizer
接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个
loss_func用来计算误差. 我们用几种常见的优化器,SGD,Momentum,RMSprop,Adam.# different optimizers opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR) opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8) opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9) opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99)) optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam] loss_func = torch.nn.MSELoss() losses_his = [[], [], [], []] # 记录 training 时不同神经网络的 loss训练
接下来训练和 loss 画图.
for epoch in range(EPOCH): print('Epoch: ', epoch) for step, (b_x, b_y) in enumerate(loader): # 对每个优化器, 优化属于他的神经网络 for net, opt, l_his in zip(nets, optimizers, losses_his): output = net(b_x) # get output for every net loss = loss_func(output, b_y) # compute loss for every net opt.zero_grad() # clear gradients for next train loss.backward() # backpropagation, compute gradients opt.step() # apply gradients l_his.append(loss.data.numpy()) # loss recoder
SGD是最普通的优化器, 也可以说没有加速效果, 而Momentum是SGD的改良版, 它加入了动量原则. 后面的RMSprop又是Momentum的升级版. 而Adam又是RMSprop的升级版. 不过从这个结果中我们看到,Adam的效果似乎比RMSprop要差一点. 所以说并不是越先进的优化器, 结果越佳. 我们在自己的试验中可以尝试不同的优化器, 找到那个最适合你数据/网络的优化器.
【Deep Learning 1】神经网络的搭建
news2026/3/3 1:52:50
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1450539.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Flutter Android开发 梳理Google Material Design颜色体系
前言
做安卓开发(Kotlin语言),Flutter开发的人员应该都听说过谷歌一直推崇的Material Design,而Material Design Color是其推崇的颜色体系,具体来说,Material Design Color是一套旨在帮助设计师和开发者创…
问题:单层工业厂房柱子吊装时,其校正的内容包括( )。 #微信#经验分享#知识分享
问题:单层工业厂房柱子吊装时,其校正的内容包括( )。
A、截面尺寸偏差
B、平面位置
C、标高
D、垂直度
E、柱的长度
参考答案如图所示
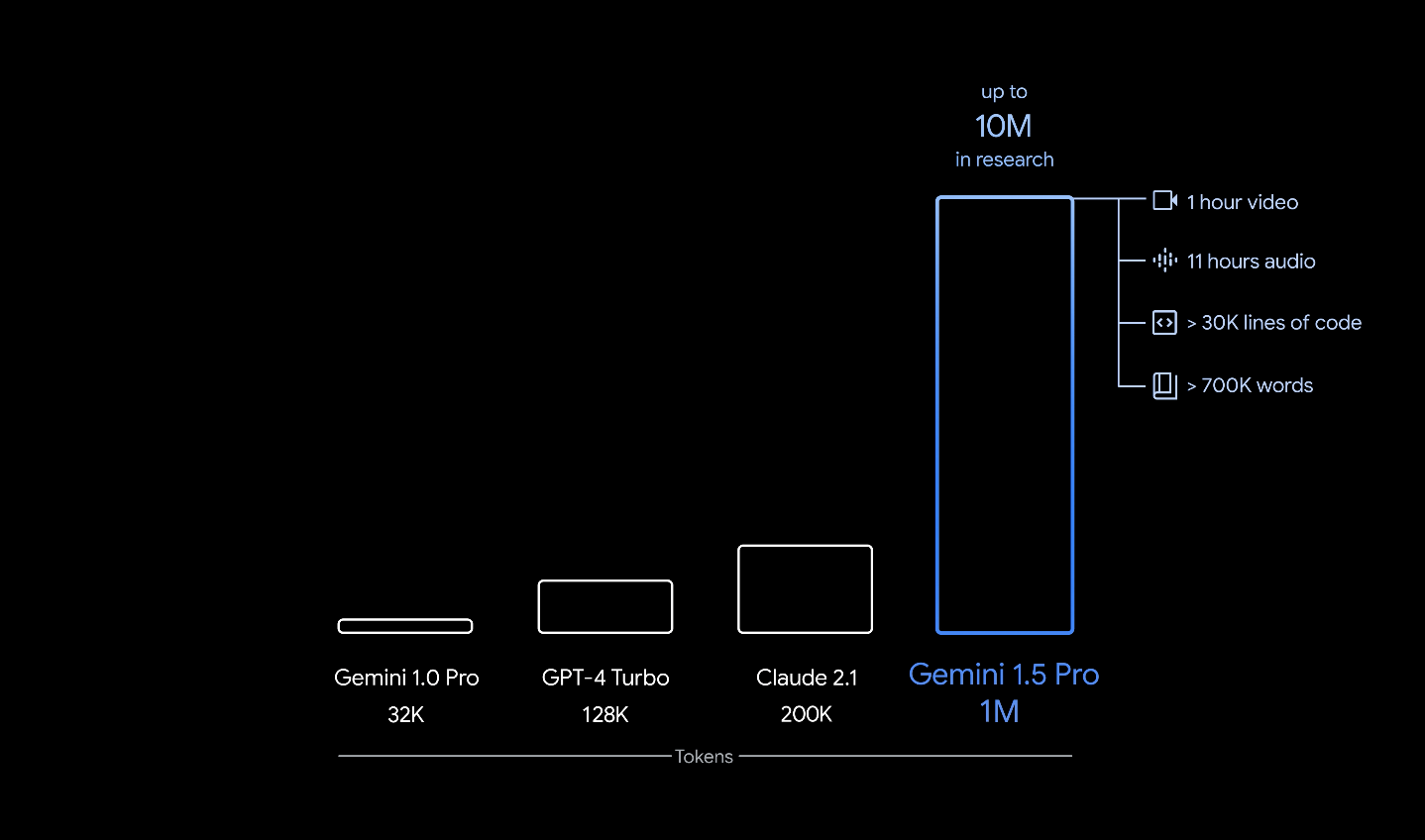
重磅更新!谷歌发布Gemini 1.5 Pro!多模态,1000K上下文!附Waitlist链接!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,所以创建了“AI信息Gap”这个公众号,专注于分享AI全维度知识…
[OPEN SQL] 修改数据
MODIFY语句用于修改数据库表中的数据
MODIFY拥有INSERT和UPDATE的操作,如果数据库表中不存在符合条件的数据则会添加该条新数据,反之数据库表中存在符合条件的数据则会更新该条数据
本次操作使用的数据库表为SCUSTOM,其字段内容如下所示 航…
【计算机网络】多路复用和多路分解
多路分解 demultiplexing 数据到达接收主机时,需要指定对应的套接字,所以在运输层报文段中放置了一些字段用于套接字的识别,从而将报文段定向到套接字,将运输层报文段数据交付到正确套接字的工作就是多路分解。多路复用 multiple…
day42 一个极简动画效果(复习相关属性)
<!DOCTYPE html>
<html><head><title>动画页面</title><style>body {font-family: Arial, sans-serif;background-color: #f2f2f2;margin: 0;padding: 0;}.container {max-width: 800px;margin: 0 auto;margin-top: 100px;padding: 20px;b…
(N-144)基于微信小程序在线订餐系统
开发工具:IDEA、微信小程序
服务器:Tomcat9.0, jdk1.8
项目构建:maven
数据库:mysql5.7
前端技术:vue、ElementUI、 Vant Weapp
服务端技术:springbootmybatisredis
本系统分微信小程序和…
ChatGPT重大升级:能自动记住用户的习惯和喜好,用户有权决定是否共享数据给OpenAI
OpenAI刚刚宣布了ChatGPT的一项激动人心的更新!
OpenAI在ChatGPT中新加了记忆功能和用户控制选项,这意味着GPT能够在与用户的互动中记住之前的对话内容,并利用这些信息在后续的交谈中提供更加相关和定制化的回答。
这一功能目前正处于测试阶…
基于PSO优化的LSTM多输入时序回归预测(Matlab)粒子群优化长短期神经网络时序回归预测
目录
一、程序及算法内容介绍:
基本内容:
亮点与优势:
二、实际运行效果:
三、 部分代码展示:
四、完整代码数据下载: 一、程序及算法内容介绍:
基本内容: 本代码基于Matalb平…
视觉slam十四讲学习笔记(五)非线性优化
已经知道,方程中的位姿可以由变换矩阵来描述,然后用李代数进行优化。观测方程由相机成像模型给出,其中内参是随相机固定的,而外参则是相机的位姿。 目录
前言
一、状态估计问题
1 最大后验与最大似然
2 最小二乘的引出
二、非…
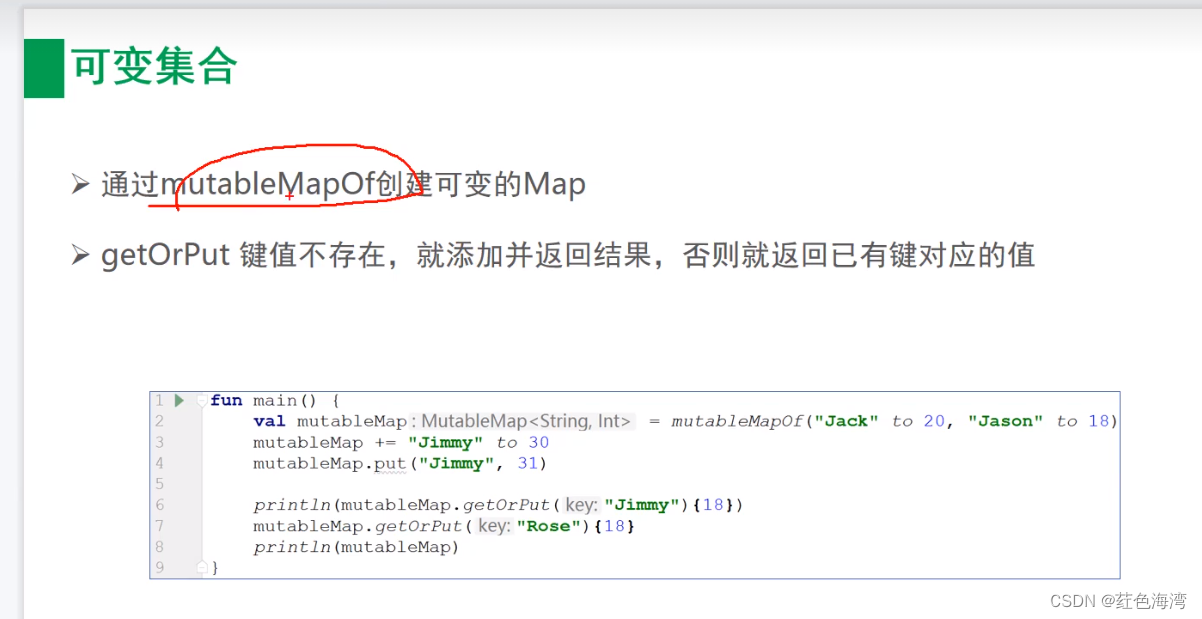
Kotlin基本语法3集合
1.List集合 1.1 只读List
fun main() {val list listOf("Jason", "Jack", "Jacky")println(list.getOrElse(3){"Unknown"})println(list.getOrNull(3)?:"Unknown")
} 1.2 可变List fun main() {val mutableList mutabl…
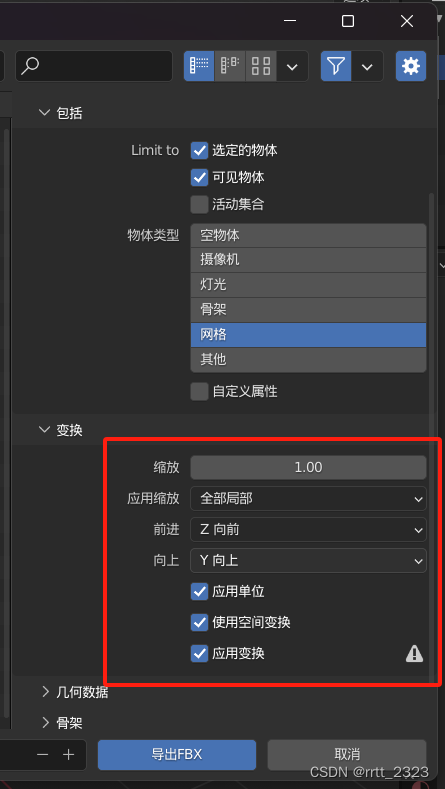
搭建 blender python api 的外部开发环境
以下都是为了不直接在 blender 的 script ide 里写脚本而做,直接在 blender 里写的话就没什么参考意义了。
首先是2个blender的设置选项,建议开启,会比较方便。 开发选项启用后,你在一些菜单上右键的话,会多出来 在线…
计算机网络——多媒体网络
前些天发现了一个巨牛的人工智能学习网站
通俗易懂,风趣幽默,忍不住分享一下给大家, 跳转到网站
小程一言
我的计算机网络专栏,是自己在计算机网络学习过程中的学习笔记与心得,在参考相关教材,网络搜素…
[职场] 面试失败的解压方式是什么 #经验分享#职场发展#知识分享
面试失败的解压方式是什么 1、心态调整:自我暗示、找人吐槽发泄情绪都是极佳的心态调整办法; 2、策略调整:当面对同一个岗位多次不成功的时候,需要我们调整策略,尝试去应聘相近的工作岗位; 3、总结提升&…
边缘计算:重塑数字世界的未来
引言 随着物联网(IoT)设备的激增和5G网络的普及,我们正站在一个计算模式的新纪元门槛上——边缘计算。这一技术范式将数据处理和分析推向网络的边缘,即设备或终端,为实时性要求较高的应用提供了前所未有的可能性。 目…
高级感的网站首屏页面,气质拿捏死死的。
高级感是客户对设计师灵魂的拷问,对于高级感的解读那真是千人千面。我尝试发一些国外的高级感首屏页面,总结出高级感的接特征。
图片要高清,精美,主题突出,有冲击力文字要有层次和对比度,尤其是大小对比和…
ESP32学习(4)——电脑远程控制LED灯
1.思路梳理 首先需要让ESP32连接上WIFI 然后创建udp socket 接着接收udp数据 最后解析数据,控制LED
2.代码实现
import network
from socket import *
from machine import Pin
p2Pin(2,Pin.OUT)def do_connect(): #连接wifi wlan network.WLAN(network.STA_IF)…
淘宝项目实战相关知识点
淘宝各个方面的布局大部分都是常规操作,在这里我就简单记录一下练习过程中的相关知识点,比较简短。相关知识点如下: 行高的取值 假设font-size为16px line-height:normal; line-height:1.5;24px,先继承后计算 line-height:200%;3…
[office] Excel CHITEST 函数 使用实例教程 #媒体#知识分享#其他
Excel CHITEST 函数 使用实例教程
提示
此函数已由 CHISQ.TEST 函数替换,新函数可以提供更好的精确度,其名称更好地反映其用法。旧函数仍可用于与早期版本Excel 的兼容。但是,如果不需要向后兼容,那么应考虑直接使用新函数&…
51单片机编程基础(C语言):LED点阵屏
点阵屏介绍 类似于数码管,要用到肉眼视觉效应。扫描,才能把每一个LED都能选中,从而显示我们想要的图形,否则, 只能一次点亮一个LED,
LED使用
51单片机点阵屏电路图: 实际连接顺序如下图&#…

![[OPEN SQL] 修改数据](https://img-blog.csdnimg.cn/direct/a275ec0c8bb44cae93bbd67bb39bb922.png)





![[职场] 面试失败的解压方式是什么 #经验分享#职场发展#知识分享](https://img-blog.csdnimg.cn/img_convert/13872b155dc597139593e2c62a2f92ae.jpeg)



![[office] Excel CHITEST 函数 使用实例教程 #媒体#知识分享#其他](https://img-blog.csdnimg.cn/img_convert/72480a7f0328615b4d14d99752204d89.png)
