你可能已经更新了操作系统以修复错误或使用最新功能。但是,如果Windows在更新后无法启动呢?
如果你面临这样的问题,主要是由于安装文件中的错误或你的系统与最新更新不兼容。此外,损坏的MBR或驱动程序也会阻止电脑启动。
不管是什么原因,本文将用十种简单的技术来指导你修复最近更新后无法启动的Windows。
为什么Windows在更新后无法启动
一些Windows用户在更新计算机后遇到了不同的问题,有时你的电脑会变得迟缓,启动缓慢,引发内核死机,等等。因此,如果你在更新操作系统后遇到困难,我们建议你执行系统还原。
同样,一些用户抱怨他们的Windows无法启动。事实上,这种情况可能由于多种原因而发生,而且很难确定确切的问题。
尽管如此,以下可能是你面临此问题的主要原因:
-
Windows更新文件已损坏或不兼容
-
启动错误
-
损坏的启动扇区(MBR)
-
损坏的Windows操作系统文件和驱动程序
-
挂起的XML文件
如何修复更新后Windows无法启动的问题
如果你的电脑没有启动,卡在黑屏上,或者在启动后经常触发蓝屏死机错误,你可以在继续进行主要修复之前尝试常规修复。
首先,我们建议强制关闭你的电脑并重新启动。这将删除可能阻止Windows启动的不需要的临时文件。
如果不起作用,请再次强制关闭电脑。然后,拔下所有USB设备(键盘、鼠标、扬声器、耳机)并打开电脑电源。这样,Windows就不必测试外围设备是否正常工作,并且很可能会启动。
现在,如果上述两种方法都没有解决启动问题,你可以继续进行下面的十个修复。
卸载最新更新
Windows可能在最近的更新后无法启动,主要是因为你的电脑不支持最新的安装文件。此外,更新中可能存在损坏重要Windows文件的错误。
因此,消除此问题的最佳方法是从Windows恢复环境中卸载更新文件:
1、首先,强制关闭你的Windows PC或笔记本电脑。
2、接下来,打开电脑并再次强制关闭。通常,这样做三次将启动自动修复。
3、现在,选择高级选项以进入恢复控制台。
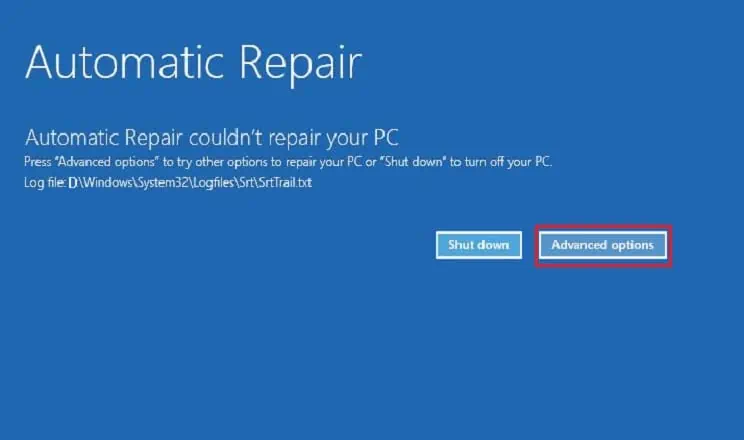
4、在“选择选项”窗口下,切换到“疑难解答”选项。
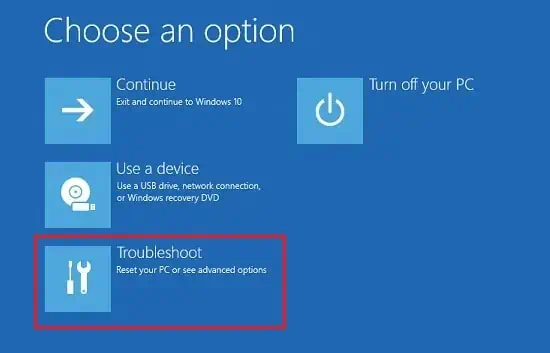
5、然后,单击高级选项。

6、在此处,选择“卸载更新”选项以删除最近安装的质量或功能Windows更新。