缺角正方形网格的铺地砖问题
“挑战难题:多米诺骨牌与无法覆盖的方格”
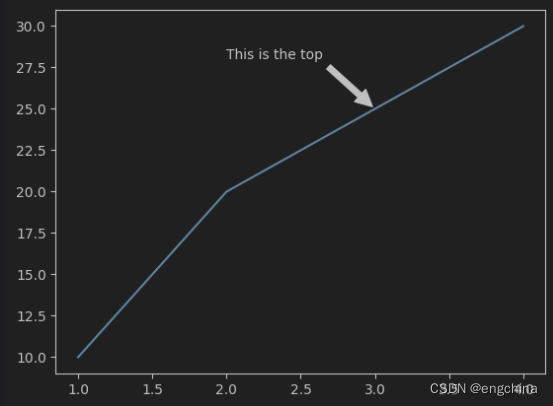
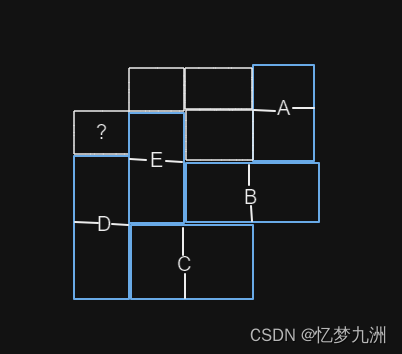
这里有个著名的难题。画八横八纵正方形网格,去掉相对的两个角。你能用多米诺骨牌形状的地砖——每一块正好覆盖两个相邻方格,把剩余部分覆盖吗?我在下图中表明,如果用四横四纵来代替八横八纵,你是办不到的。假设你决定用一块地砖覆盖我图中标为A的区域,那么容易看出,你必须还要把地砖放到B、C、D和E的位置上,剩下一个小方格无法覆盖。既然右上角的格子无论如何总要覆盖住,而仅剩的另一种覆盖的方式也会导致类似的问题(通过位置的对称关系),所以覆盖整个图形是不可能的。
“挑战与不可能:八横八纵方格铺设问题的解析”
如果我们用五来代替四,网格的铺设仍然是不可能的,原因很简单,每块地砖占两个方格,而小方格总数是23——是个奇数。但是
8
2
−
2
=
62
8^2-2=62
82−2=62是个偶数,所以我们不能把这样的论证用于八横八纵的方格。另一方面,若想找到一种类似于刚才四横四纵情况中我给的证明,你很快就会放弃,因为你所需要考虑的可能情况实在太多了。那对这个问题应该怎样入手呢?如果你从没接触过这个问题,我强烈建议你在继续阅读之前先尝试求解一下,或者暂时跳过下一段,因为如果你解决了它,你将能够对数学中的愉悦感有很好的理解。
对于无视我建议的读者——经验表明这些人占大多数,有一个词几乎可以代表全部证明:国际象棋。国际象棋的棋盘是八横八纵的方格。每个小格交错地填上黑色和白色(就象棋游戏本身来考虑似乎并不是必要的,不过能够使视觉看起来更轻松)。两个对顶角方格颜色是相同的。如果它们都是黑色的,那么一旦把它们去掉,剩下的棋盘就有32个白格子和30个黑格子。每一块骨牌只能覆盖两种颜色的方格各一块,所以一旦你放进了30块骨牌,无论是怎么放的,最终都必然剩下两个白方格,它们是无法覆盖的。
“证明之美:数学中的思想与探索”
这个简短的论证极好地表明,证明何以能够不仅仅保证陈述的正确性。例如,四乘四方格去掉两个对顶角无法被覆盖,这条陈述我们现在有了两种证明。一种是我前面给出的,另一种是四乘四版本的象棋盘论证法。这两种证明都得到了我们想要的结果,但只有第二种给了我们一种关于无法覆盖的类似推理的东西。这样的推理能够立即告诉我们,一万乘一万的方格去掉相对的两角也是无法覆盖的。第一种论证则只能告诉我们四乘四的情况。
第二种论证有个值得瞩目的特征,它完全依赖于一种思想,这种思想虽出人意料,但一经理解便显得非常自然。人们经常很困惑,为什么数学家有时会用“优美”、“漂亮”甚至“绝妙”来形容一些证明。这样的例子就让我们对其含义有了一点理解。音乐也能够提供一个有用的类比:一段乐曲刚开始可能沿意想不到的和声方向行进,过后却感觉非常完美恰当,或者一段管弦织体呈现出整体大于部分之和的境界,其方式我们还无法全然理解一一每当这些时候我们就会为之陶醉。在数学证明中,有突如其来的启发,有出人意料却自然而然的思想,还有引人入胜、有待进一步发掘的暗示,这些都能够给我们带来类似的偷说感。当然,数学的美不同于音乐的美,可音乐的美同样也不同于绘画的美、诗歌的美、姣好面容的美。
总结
缺角正方形网格的铺地砖问题是一个著名的数学难题。无论是八横八纵的方格还是用其他尺寸的方格,都无法用多米诺骨牌形状的地砖完全覆盖剩余部分。通过类比国际象棋的棋盘,我们可以利用颜色交错的方格来证明无法覆盖剩余的小方格。这个问题的解析展示了数学证明的美妙之处,其中包括意外的思想、引人入胜的推理和待探索的暗示。这种美妙的证明过程使我们对数学的思维方式和探索过程产生了更深入的理解。
无论是数学、音乐、绘画还是诗歌,每种形式都有其独特的美,而数学证明中的美妙之处也展现了数学的独特之美。






![Cocos2dx-lua ScrollView[一]基础篇](https://img-blog.csdnimg.cn/direct/8d35bd370b854f478e54a7fd86f165b8.png)