目录
树的定义:
深度和高度:
二叉树
由来
二叉树种类:
满二叉树:
完全二叉树:
严格二叉树(Strict Binary Tree):
平衡二叉树(Balanced Binary Tree):
存储结构(顺序存储和链式存储)
顺序存储
优点:
缺点:
链式存储
链式存储结构的主要特点包括:
二叉树的遍历
前序遍历
代码实现(递归):
中序遍历
代码实现(递归):
后序遍历
代码实现(递归):
层序遍历有点复杂,下一篇专门写这方面的总结。
树的定义:
树(层级结构)是一种重要的非线性数据结构(递归的数据结构),它由n(n≥0)个有限节点组成一个具有层次关系的集合。这些节点具有如下特性:(在一个有效的树中,如果有n个节点,就会有n-1条边。)
- 每个节点有零个或多个子节点。
- 没有父节点的节点称为根节点。根:树的最顶部的节点,唯一没有双亲的节点。
- 每一个非根节点有且只有一个父节点。
- 除了根节点外,每个子节点可以分为多个不相交的子树。
树的术语包括:
- 结点:使用树结构存储的每一个数据元素都被称为“结点”。
- 森林:多棵互不相交的树的集合称为森林。
- 有序树和无序树:如果树中结点的子树从左到右看有规定的顺序,这棵树称为有序树;反之称为无序树。
树的最常见实现方式:就是动态创建节点,用指针或者引用把他们链接起来。
如下图:
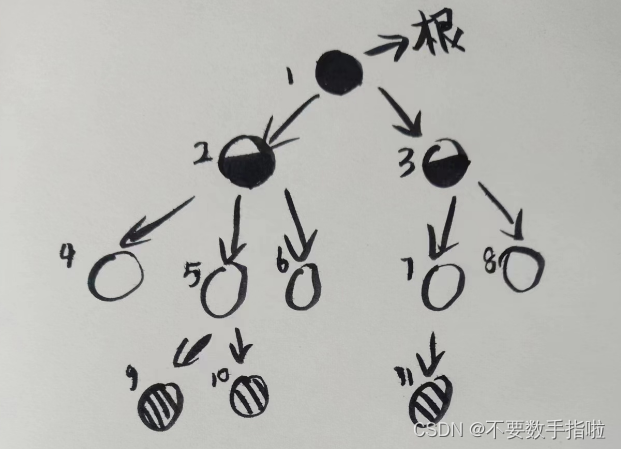

链接是有方向的,它不是双向而是单向的。当我们遍历一棵树的时候,只能从一个方向进行。
深度和高度:
树的深度(Depth):从根节点开始自顶向下逐层累加,直到最远的叶节点。换句话说,最深的叶结点的深度就是树的深度。如果有多个叶节点位于同一最大深度,那么树的深度就是这个最大深度。因此,树的深度等于树中节点的最大层次。同一深度的节点可以被称为同一级的节点。
树的高度(Height):从树的底层叶节点开始自底向上逐层累加,直到根节点。也就是说,树的高度就是从根节点到最远叶节点的最长路径长度。对于任何树,树的高度等于树的最大层数。
值得注意的是,有些教材或资料在定义树的高度时,可能会将其定义为根节点的高度,即从根节点到最远叶节点的最长路径长度减一。这种定义方式在实际应用中也较为常见。
二叉树
由来
树还有不同的类型,例如二叉树。二叉树是树型结构的一个重要类型,它的每个节点的度(即子节点的数量)不大于2。这意味着二叉树的每个节点最多有两个子节点,通常被称为左子节点和右子节点。
二叉树种类:
满二叉树:
是一种特殊的二叉树,其特点是除最后一层外,每一层上的所有节点都有两个子节点。也就是说,如果一个二叉树的深度为K,且结点总数是(2^k) -1,则它就是满二叉树。满二叉树的每一层都包含最大数量的节点,因此在给定深度下,满二叉树具有最多的节点。满二叉树是完全二叉树的特例,完全二叉树是指除最后一层外,其他层的节点数达到最大,且最后一层的节点都集中在左边。在满二叉树中,因为每一层都已经满了,所以它也是一棵完全二叉树。
完全二叉树:
是由满二叉树而引出的概念。对于深度为k的有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,这棵二叉树被称为完全二叉树。也就是说,如果对树中的结点按从上至下、从左到右的顺序进行编号,编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树就是完全二叉树。
完全二叉树的特点包括:
- 叶子结点只能出现在最下层和次下层。
- 最下层的叶子结点集中在树的左部。
- 倒数第二层若存在叶子结点,一定在右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即没有右子树。
- 同样结点数目的二叉树,完全二叉树深度最小。
需要注意的是,满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。另外,完全二叉树第i层至多有2^(i-1)个节点,共i层的完全二叉树最多有2^i - 1个节点。
严格二叉树(Strict Binary Tree):
是二叉树的一种特殊类型,它的特点是每个非终端节点(非叶子节点)都有且仅有两个子节点。也就是说,在严格二叉树中,不存在只有一个子节点或没有子节点的非终端节点。严格二叉树与满二叉树和完全二叉树有所不同。满二叉树要求除最后一层外,每一层上的所有节点都有两个子节点,而严格二叉树则只要求非终端节点有两个子节点,对叶子节点没有要求。完全二叉树则要求除最后一层外,其他层的节点数达到最大,且最后一层的节点都集中在左边,而严格二叉树则没有这个要求。
平衡二叉树(Balanced Binary Tree):
是一种特殊的二叉树,其特点是在进行插入、删除等操作后,依然能保持树的平衡性,即任何节点的两个子树的高度差的绝对值不超过1。平衡二叉树有多种实现方式,如AVL树和红黑树等。平衡二叉树的重要性在于它能够保证在最坏情况下,查找、插入和删除操作的时间复杂度都是O(log n),这对于处理大量数据非常有效。如果没有平衡性,最坏情况下二叉树可能退化为链表,导致时间复杂度变为O(n)。
存储结构(顺序存储和链式存储)
顺序存储
二叉树的顺序存储结构通常使用数组来实现。在顺序存储结构中,二叉树中的每个节点按照完全二叉树的顺序存储在一个数组中。完全二叉树的特性使得这种存储方式成为可能,因为在完全二叉树中,除了最后一层之外,其他层的节点数都是满的,并且最后一层的节点都集中在左边。
对于任意一个在数组中的位置为i的节点,其左孩子节点的位置可以通过计算 2i+1 得到,其右孩子节点的位置可以通过计算 2i+2 得到。同样地,对于任意一个位置为j的孩子节点,其父节点的位置可以通过计算 (j-1)/2 得到。
优点:
顺序存储结构的优点是可以快速地访问任意节点,因为每个节点都有一个固定的数组索引。
缺点:
这种存储方式的缺点也很明显,即它可能会浪费存储空间。因为在二叉树中,如果节点数较少,那么数组中的很多位置可能都是空的。此外,对于非完全二叉树,这种存储方式也无法直接表示。
总的来说,顺序存储结构适用于完全二叉树或者节点数较多的二叉树。对于其他类型的二叉树,或者节点数较少的二叉树,链式存储结构可能是一个更好的选择。
链式存储
链式存储结构,又称为链接存储结构,是一种数据的存储方式。
在这种结构中,每个数据元素(通常称为节点)除了包含自身的信息(称为信息域)外,还包含指向其逻辑关系中的下一个节点的指针(称为指针域)。因此,每个节点都通过其指针域与其逻辑关系中的下一个节点相连。这种存储方式不要求逻辑上相邻的元素在物理位置上也相邻,因此它没有顺序存储结构所具有的弱点。
链式存储结构的主要特点包括:
- 存储密度比顺序存储结构小,因为每个节点都需要额外的存储空间来存储指向下一个节点的指针。
- 插入和删除操作灵活,节点可以被插入到链表的任何位置,包括首、中、末,而且不需要移动其他节点中的指针。
- 链表的大小可以按需伸缩,是一种动态存储结构,因此在增加或删除元素时性能更高。
- 查找节点时的效率相对较低,因为只能从第一个节点开始逐个查找,直到找到所需的节点。
总的来说,链式存储结构是一种非常有用的数据结构,特别适用于需要频繁进行插入和删除操作的情况。然而,由于其查找效率相对较低,因此在需要频繁查找的情况下可能不是最佳选择。
二叉树的遍历
二叉树的每个节点都只会被访问一次。
二叉树有一个前驱和两个后继。
二叉树的遍历顺序有4种,分别是:前序遍历,中序遍历,后序遍历和层序遍历。
前序遍历
先访问根节点,再访问左右子树。
运动轨迹如下:

代码实现(递归):
void Tree(Tree* root) {
if (root == NULL) {
return;
}
printf("%d", root->data);
Tree(root->L_ch);
Tree(root->R_ch);
}中序遍历
先访问左子树,再访根节点,最后访问右子树。
运动轨迹如下:
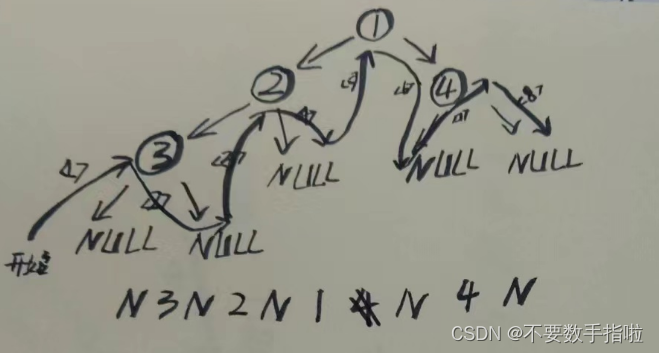
代码实现(递归):
void Tree(Tree* root) {
if (root == NULL) {
return;
}
Tree(root->L_ch);
printf("%d", root->data);
Tree(root->R_ch);
}后序遍历
先左子树,再右子树,最后根节点。
运动轨迹如下:

代码实现(递归):
void Tree(Tree* root) {
if (root == NULL) {
return;
}
Tree(root->L_ch);
Tree(root->R_ch);
printf("%d", root->data);
}