C++:priority_queue模拟实现
- 什么是priority_queue
- 模拟实现
- 向上调整算法
- 向下调整算法
- 插入与删除
- 仿函数
什么是priority_queue
priority_queue称为优先级队列。优先级队列是一种特殊的队列,其中每个元素都有一个相关的优先级。元素的优先级决定了它们在队列中的顺序。具有较高优先级的元素在队列中被排在前面,而具有较低优先级的元素在队列中被排在后面。
可以简单理解为,priority_queue其实就是堆,如果作用于整型,可以让最大/最小的数字处于堆顶,而其也可以作用于其它类型,比如作用于string,那么可以根据字典序来排序。
接下来我带大家实现一下这个结构:
模拟实现
在STL中,preority_queue是一个容器适配器,因为其只要求了数据按照指定的顺序排列,但是没有对底层结构做要求,所以我们直接用其他容器做底层即可。
在此我使用了vector做底层,因为在优先级队列中,我们需要频繁地进行下标访问,使用deque也是可以的。
基本结构:
template <class T, class Container = vector<T>>
class preority_queue
{
private:
Container _con;
};
模板参数:
T:这个优先级队列承载的元素类型
Container:底层容器类型,此处默认值为vector
我们看看preority_queue有哪些接口:
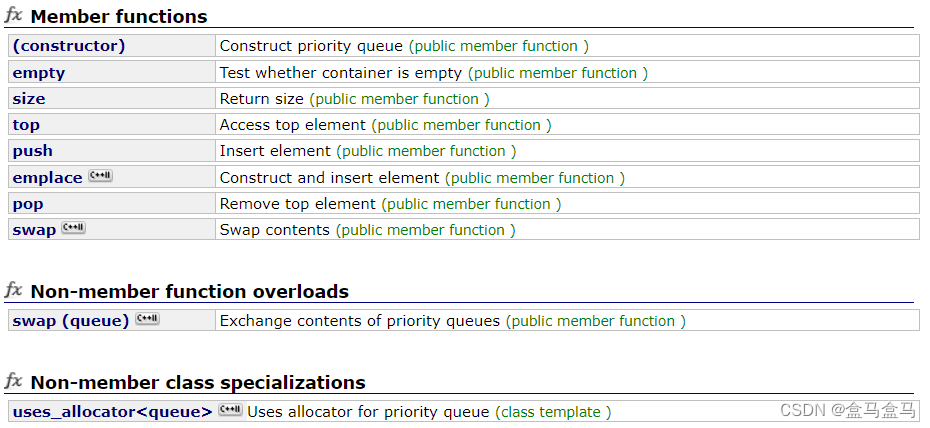
接下来我们一一实现:
top:
想要得到preority_queue优先级最高的元素,其实就是拿到vector的第一个元素_con[0]。
const T& top()
{
return _con[0];
}
size:
preority_queue的大小,就是vector的大小。
size_t size()
{
return _con.size();
}
empty:
判断preority_queue是否为空,就是判断vector是否为空。
bool empty()
{
return _con.empty();
}
向上调整算法
现在假设我有以下堆结构:
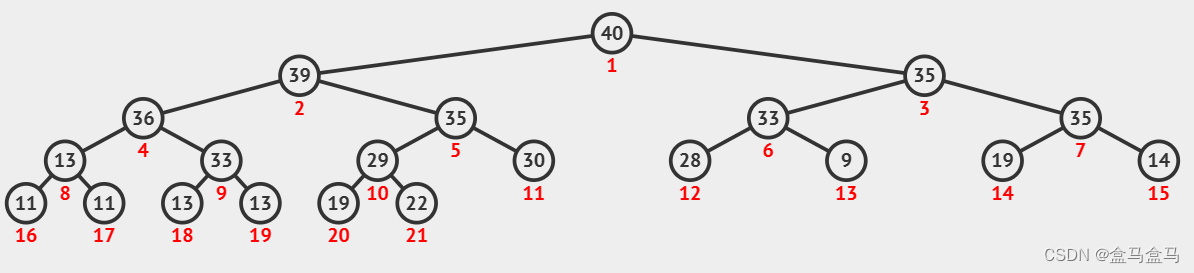
我现在在堆尾部插入一个数据,如何将数据调整到合适的位置,保证这个结构依然满足堆的要求?
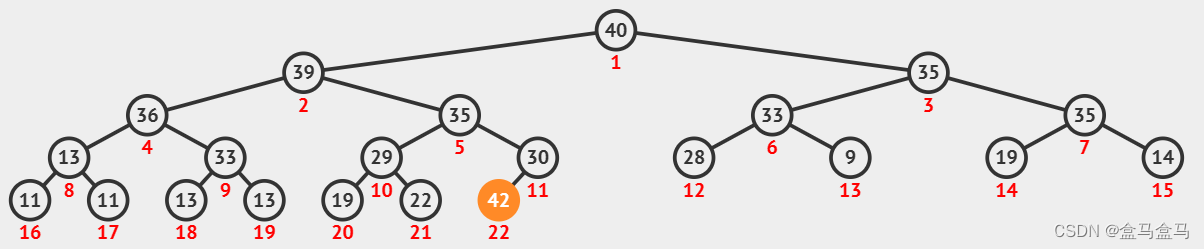
想要将其插入到指定位置,就要使用到向上调整算法:将最后一个节点向上调整到合适的位置。
首先讲解一个公式:堆结构中父节点与子节点的下标关系
假设父节点的下标为
parent,则其左子节点的下标为 2 *parent+1,右子节点的下标为 2 *parent+2。
由于大堆要保证每隔父亲节点大于两个子节点,而除去最后一个节点,其它的节点已经满足堆结构了,所以此处需要将最后一个节点不断地与其父亲节点比较,如果其比父亲节点大,就交换位置,然后继续和新的父亲节点比较,直到比当前的父亲节点小,或者到达堆顶为止。
图示:
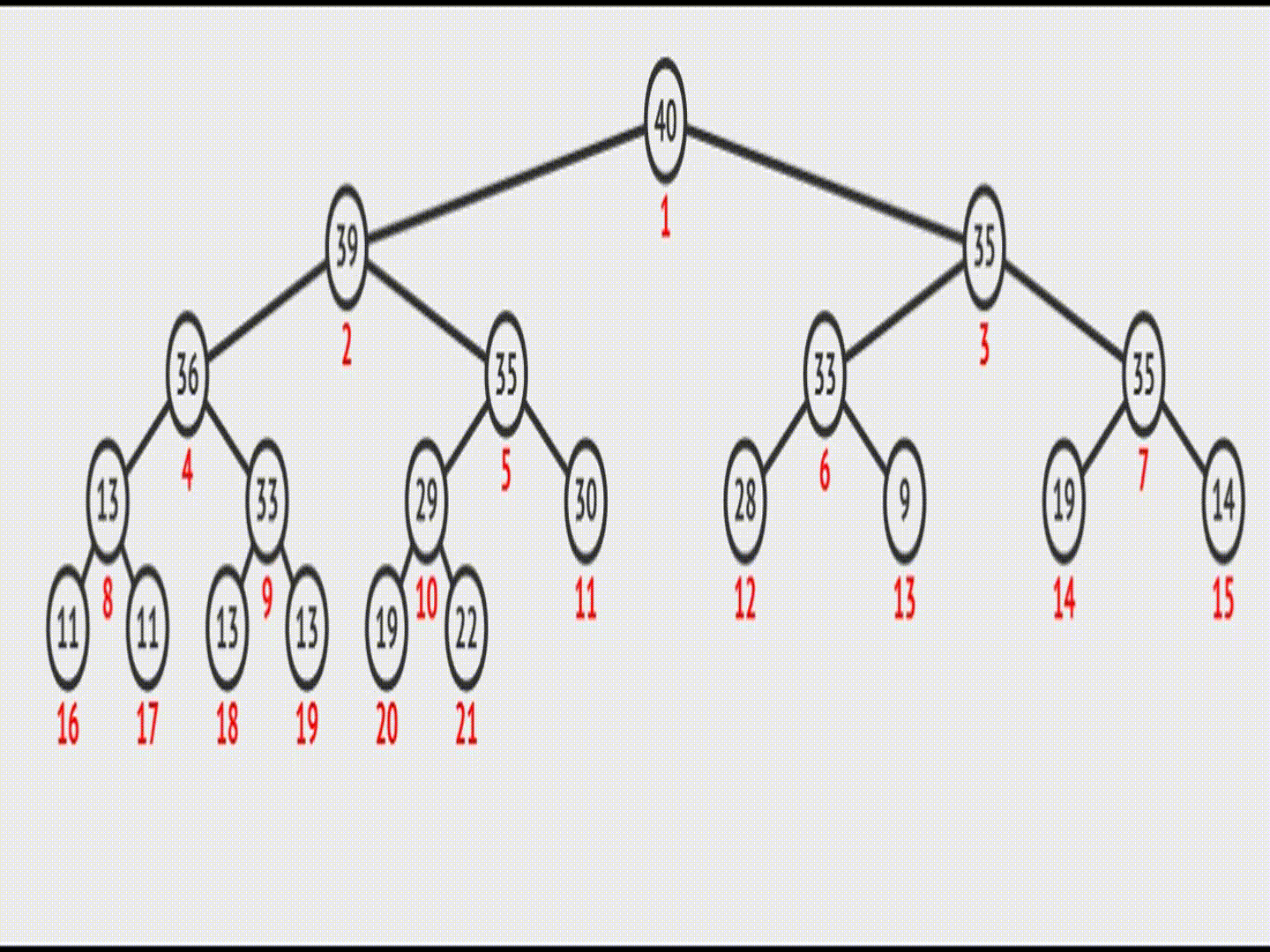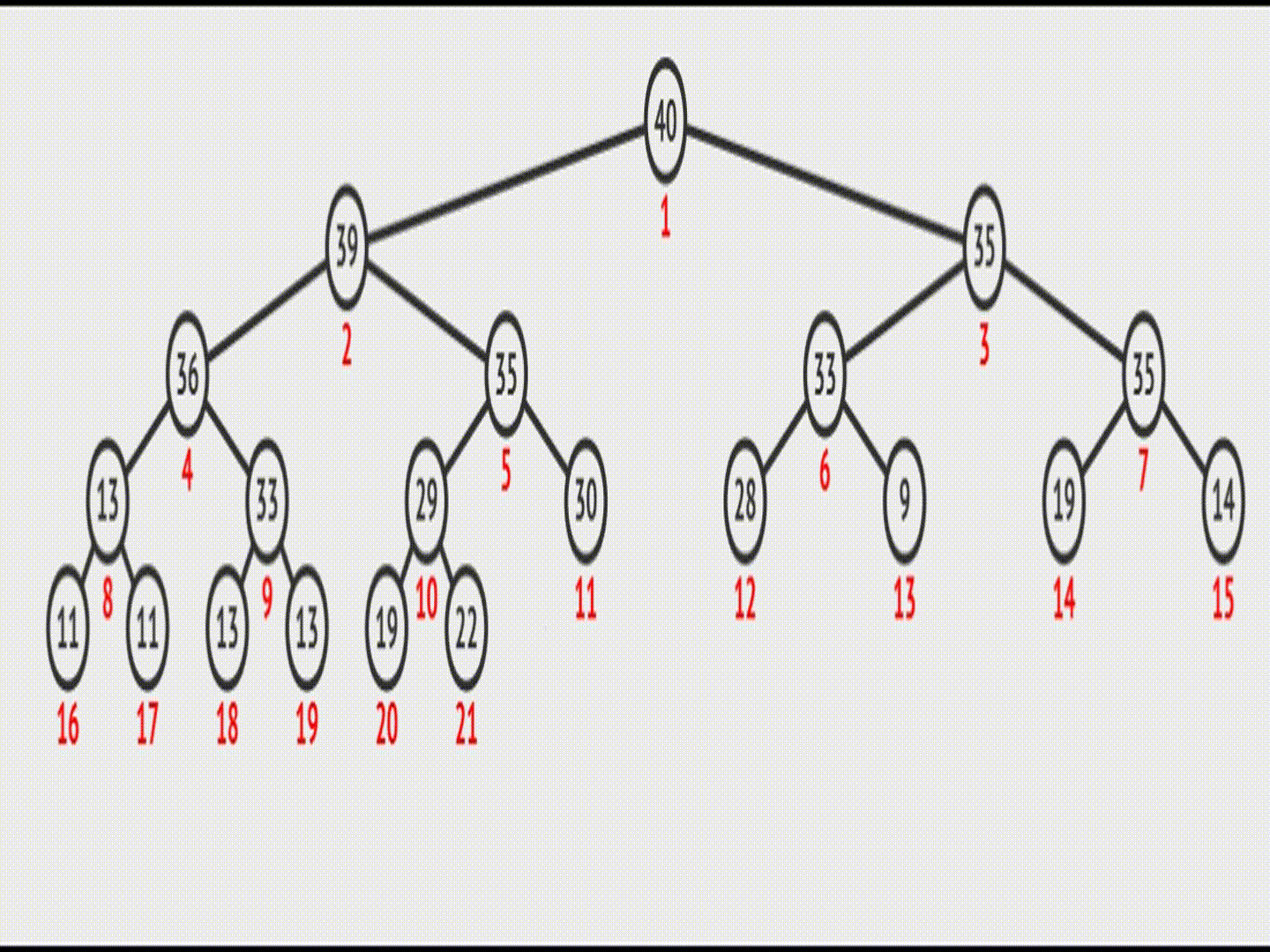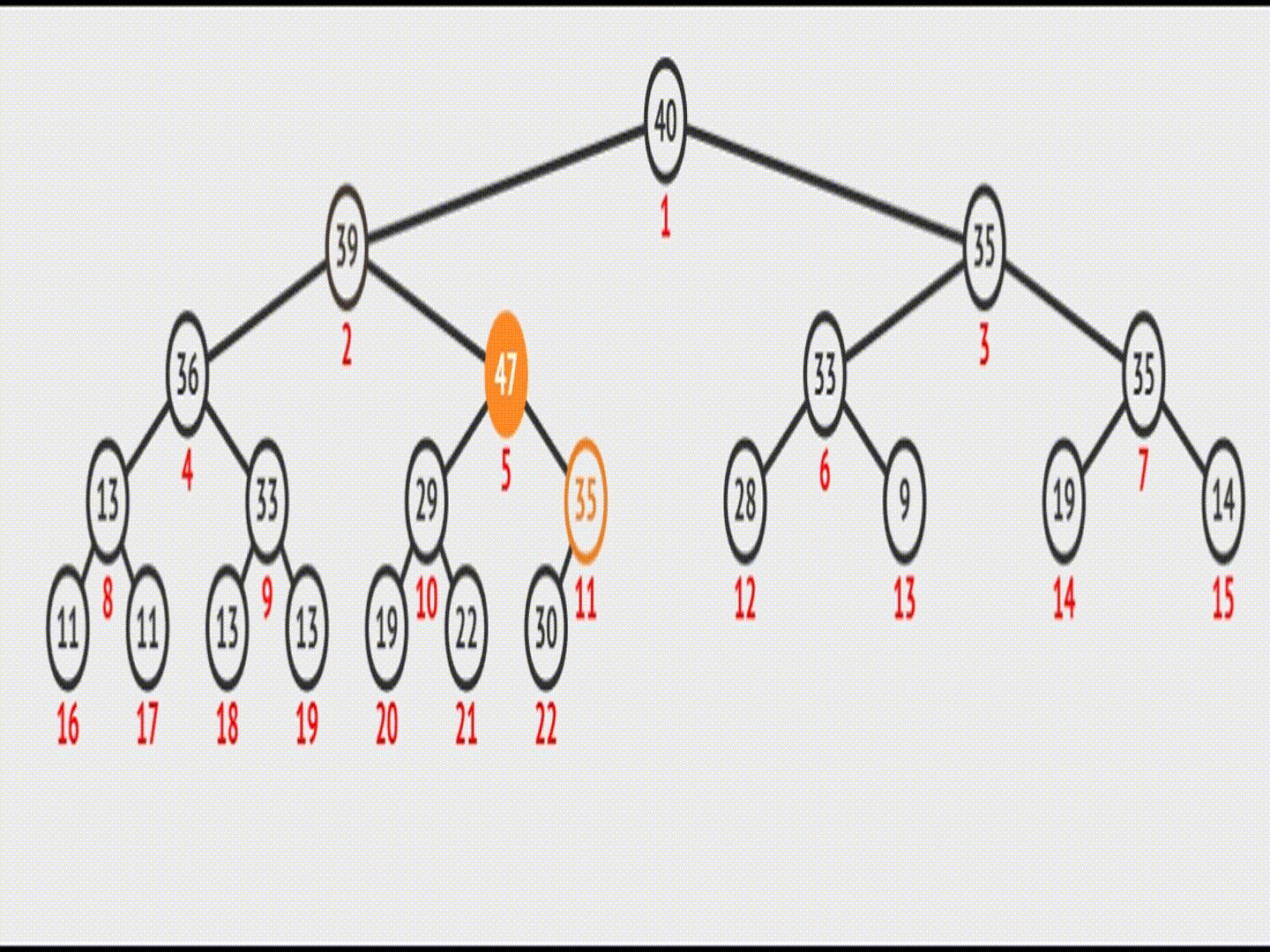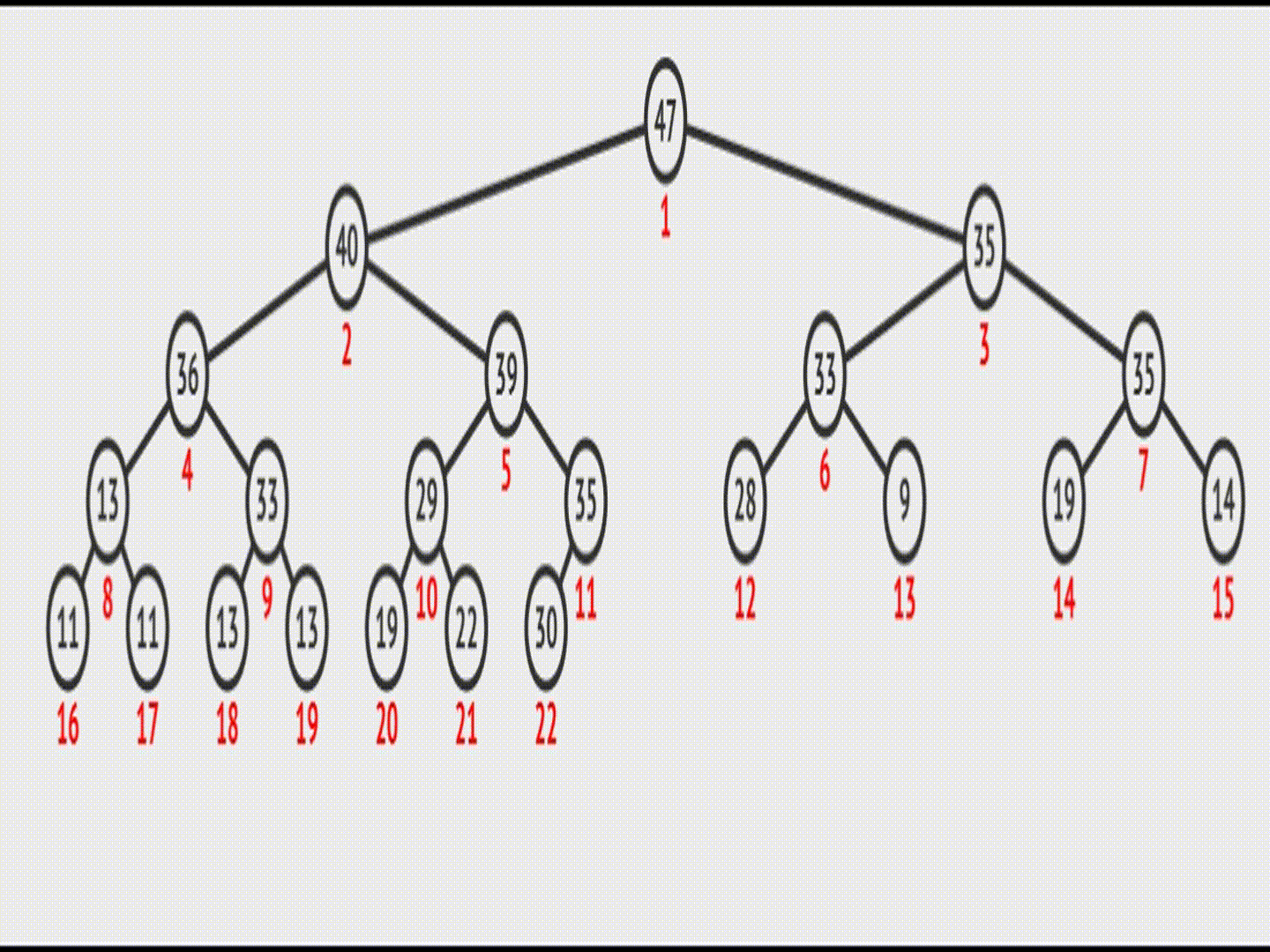
在vector中的效果(实际效果):
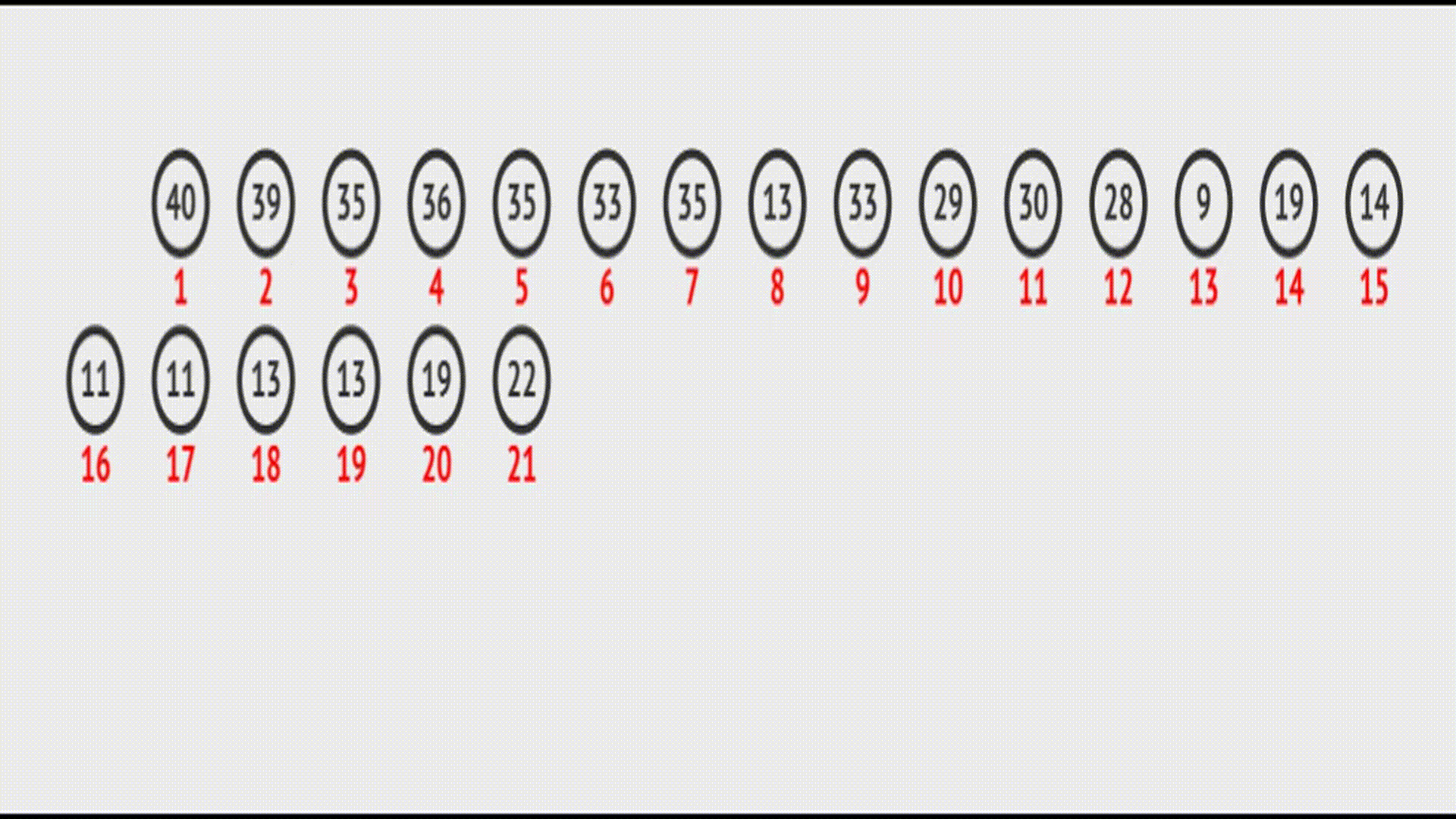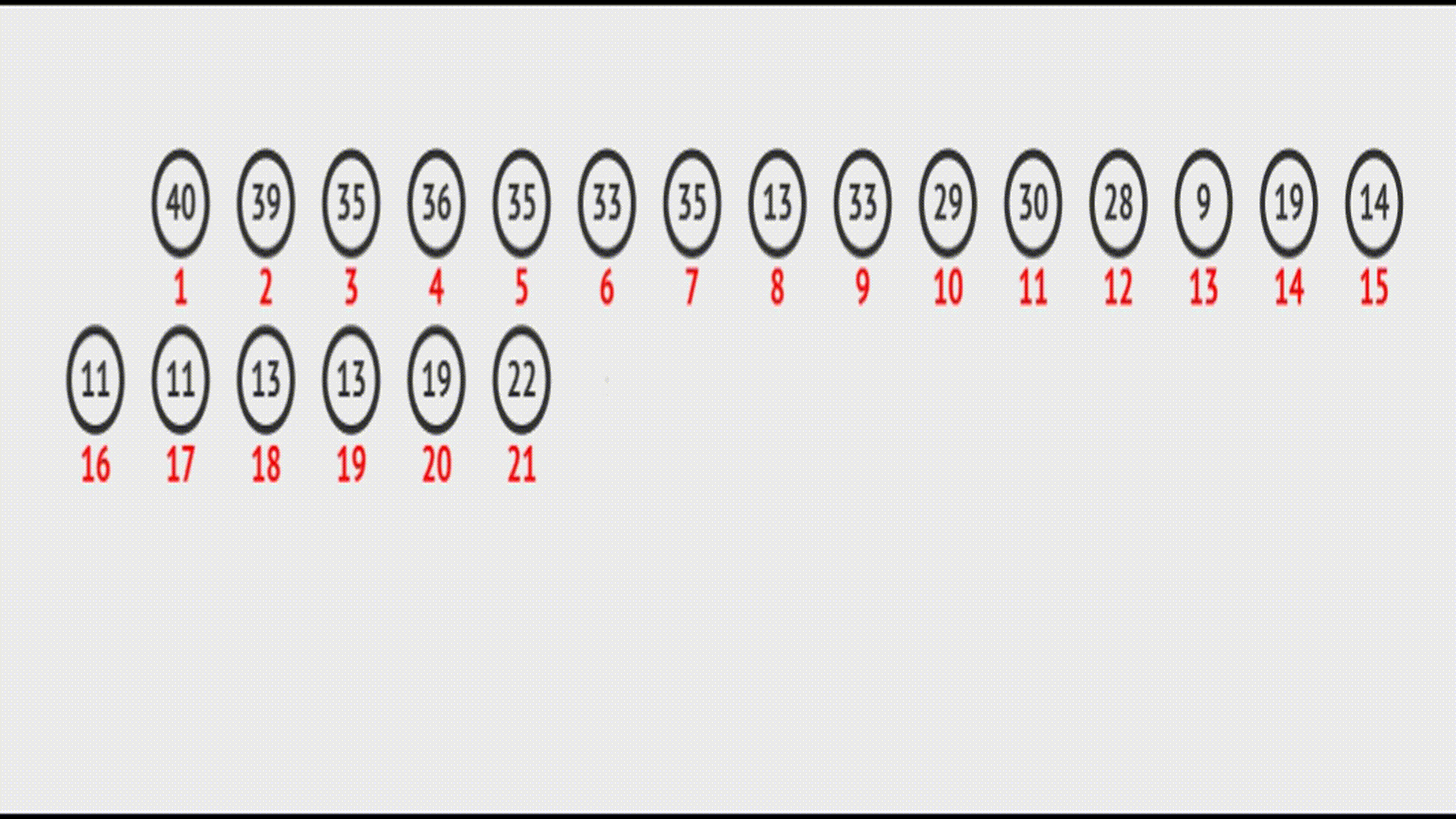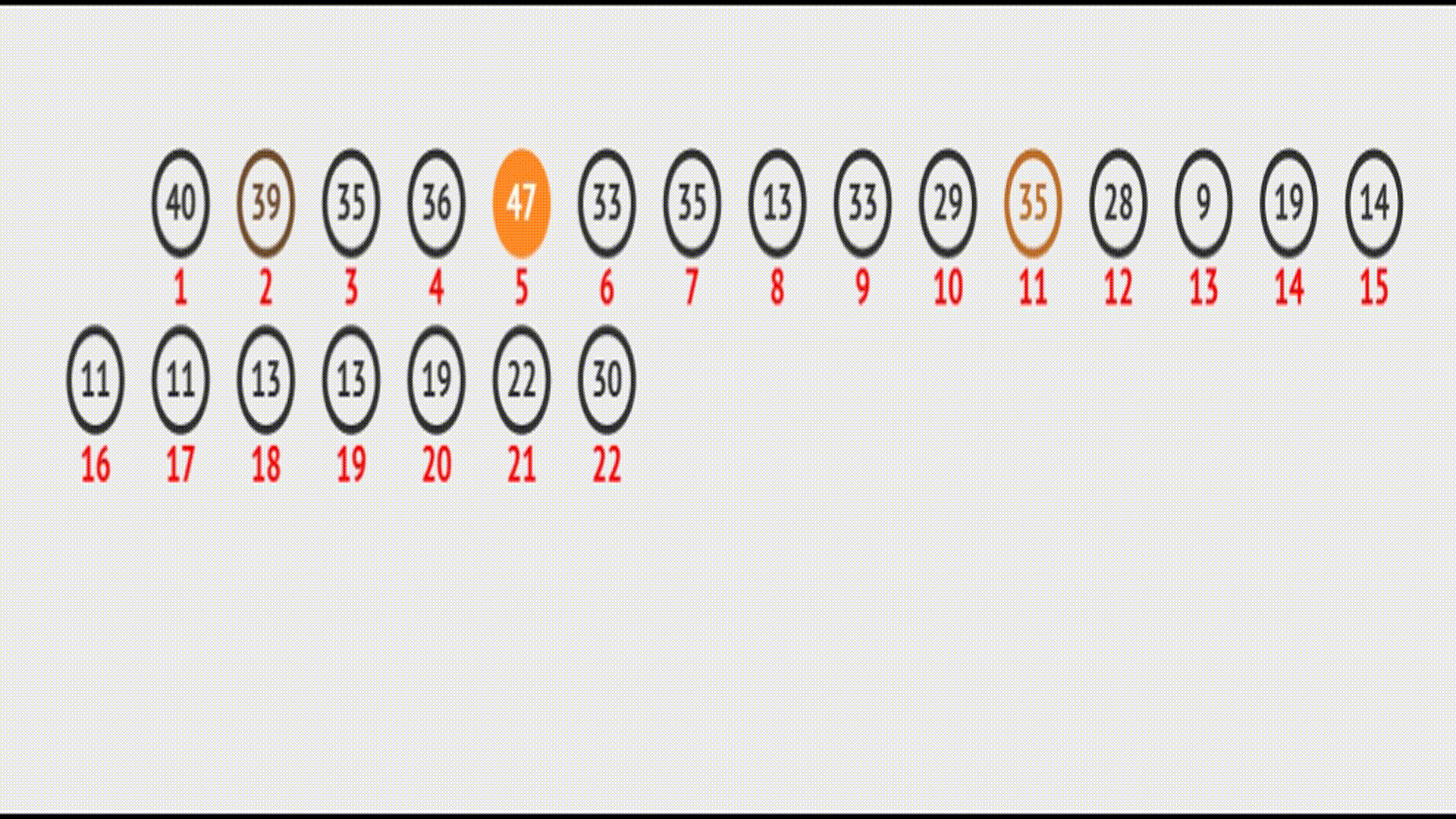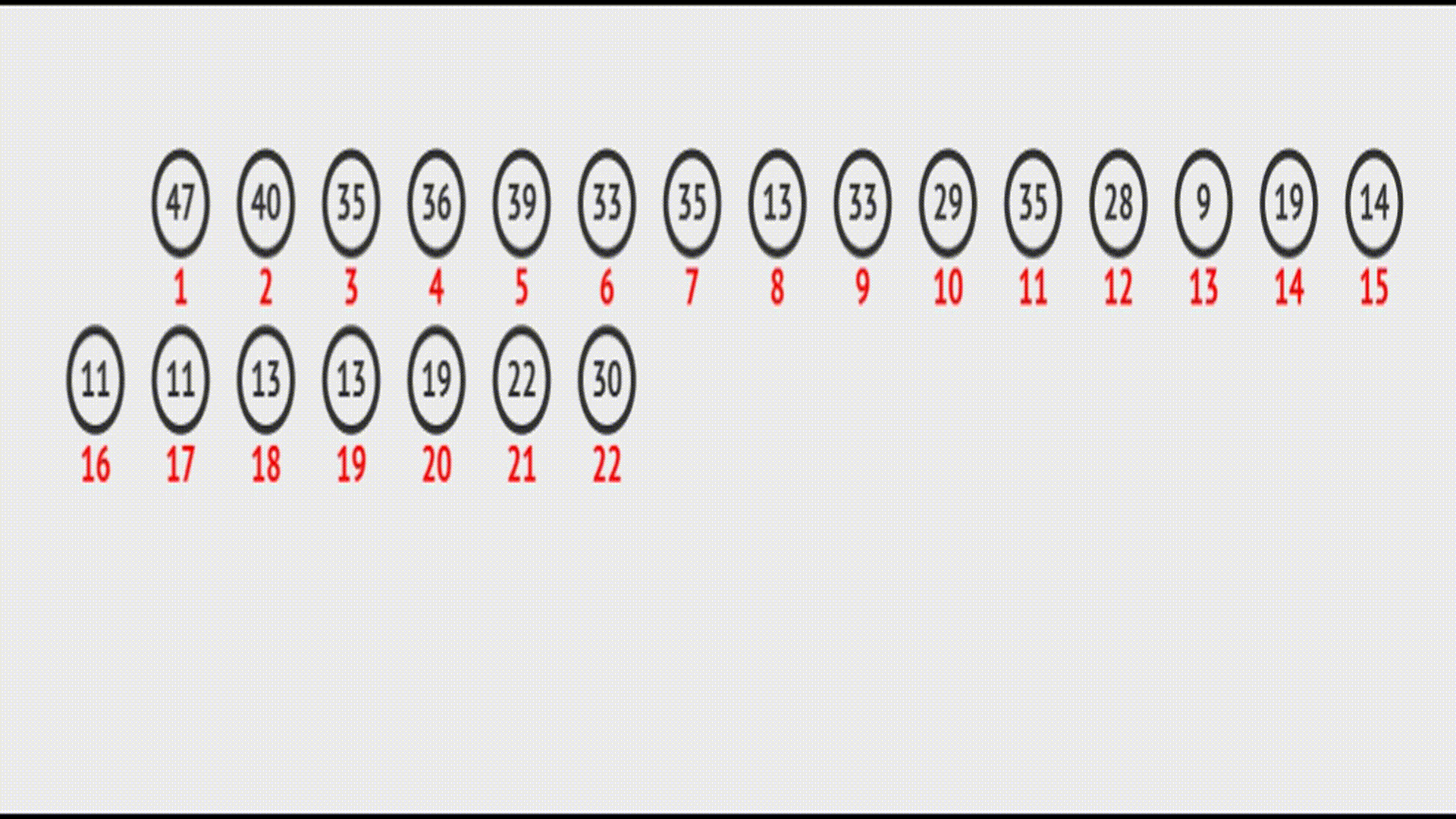
代码实现:
void AdjustUp(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_con[child] > _con[parent])
{
Swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
代码详解:
- 定义父节点索引:
int parent = (child - 1) / 2;
根据完全二叉树的性质,节点i的父节点索引是(i - 1) / 2,所以计算出child节点的父节点索引。
- 进入循环:
while (child > 0)
当child大于0时,继续执行循环。循环的目的是将child节点与其父节点进行比较,并根据需要进行交换。
- 比较
child节点与其父节点的大小:
if (_con[child] < _con[parent])
如果child节点的值小于其父节点的值,说明需要进行交换。这是一个小堆的向上调整操作。如果想要实现大堆的向上调整,需要将判断条件改为>。
- 交换节点值和更新索引:
Swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
交换child节点和父节点的值,然后更新child和parent的值,使其指向交换后的节点。
- 循环结束:
else
{
break;
}
如果child节点大于等于其父节点,说明调整完成,跳出循环。
通过这个向上调整的操作,可以将新插入的元素调整到合适的位置,以保证堆的性质。
向下调整算法
如果堆中某个节点的值被修改,如何调整这个堆的结构保证其依然满足堆的要求?
当堆中的某个节点的值发生改变时(例如,该节点的值被修改),需要进行向下调整操作来保持堆的性质。
向下调整的基本思想是将当前节点与其子节点进行比较,并根据堆的类型(大堆或小堆)选择合适的交换操作。如果当前节点的值小于(或大于)其子节点的值,那么需要将当前节点与其子节点中的较大(或较小)值进行交换。然后,继续向下调整交换后的子节点,直到满足堆的性质为止。
示意图如下:
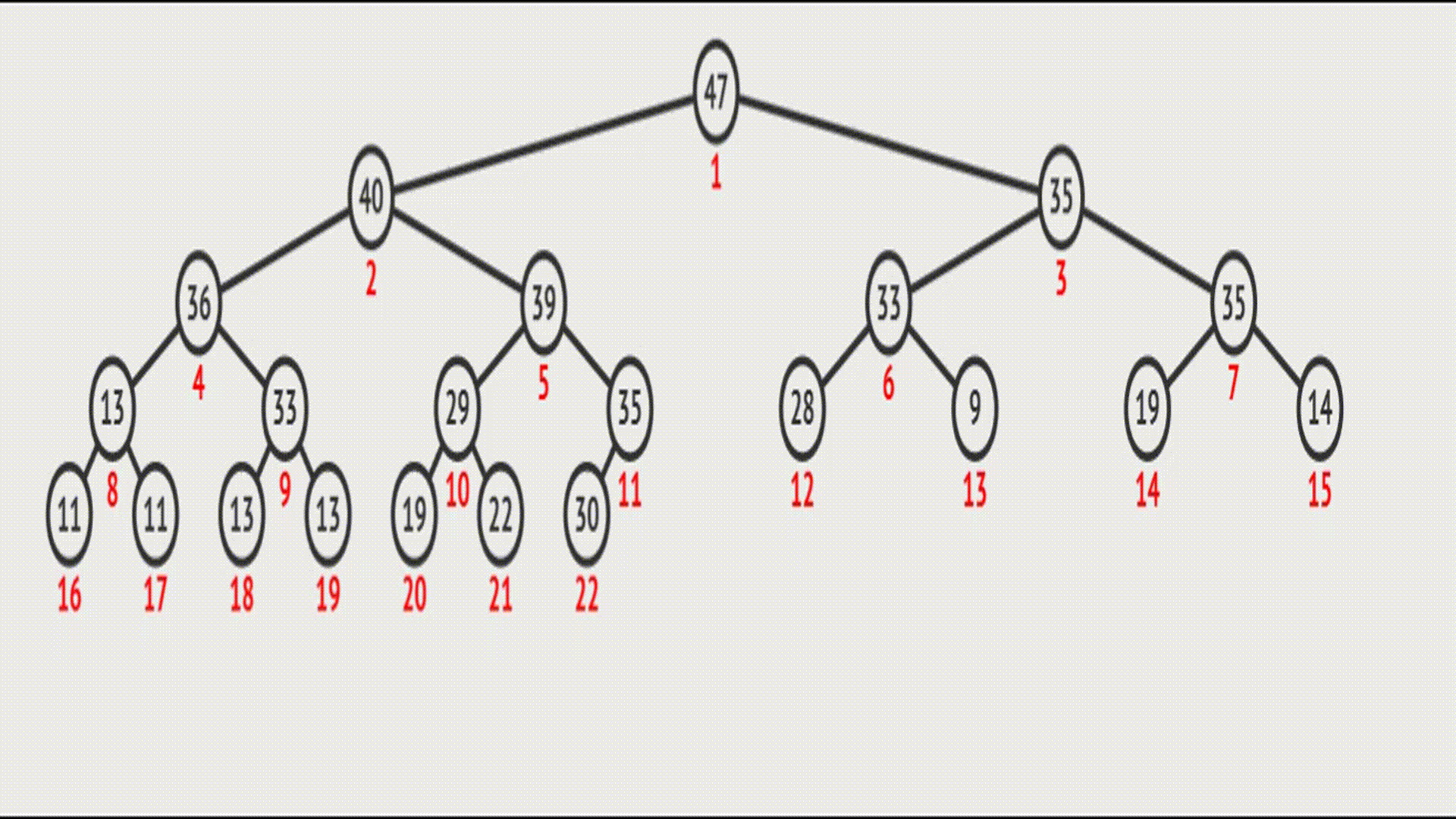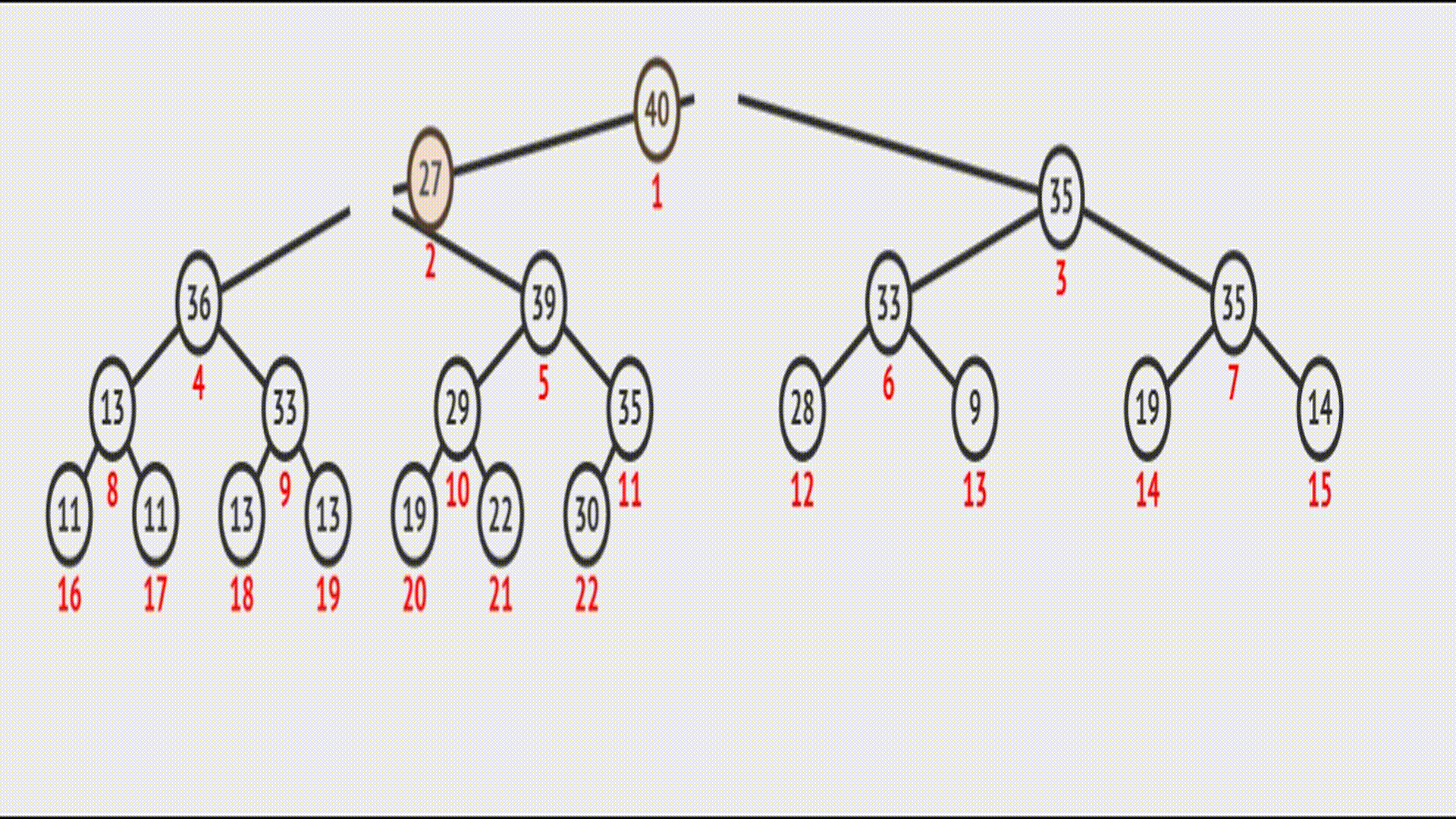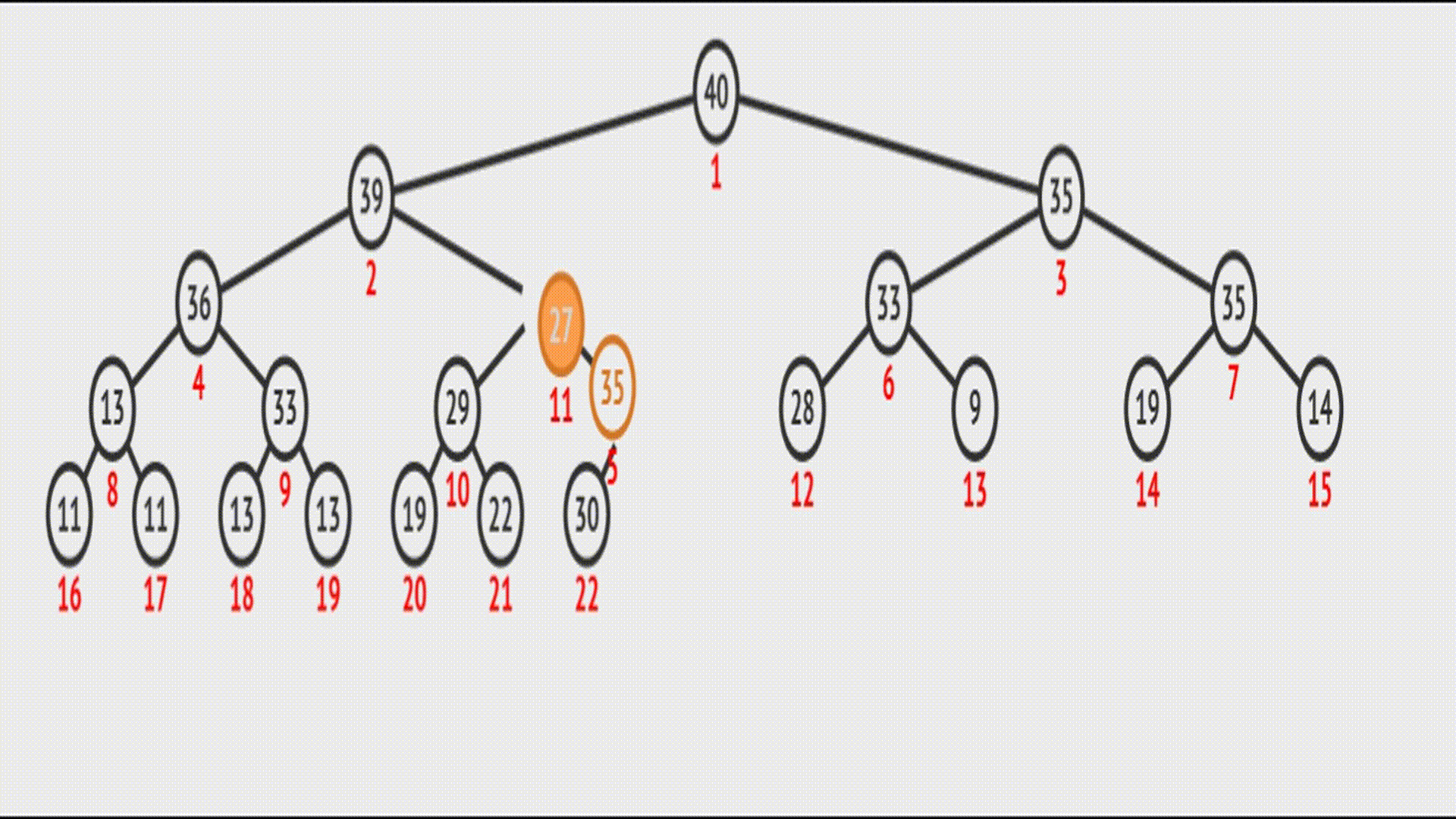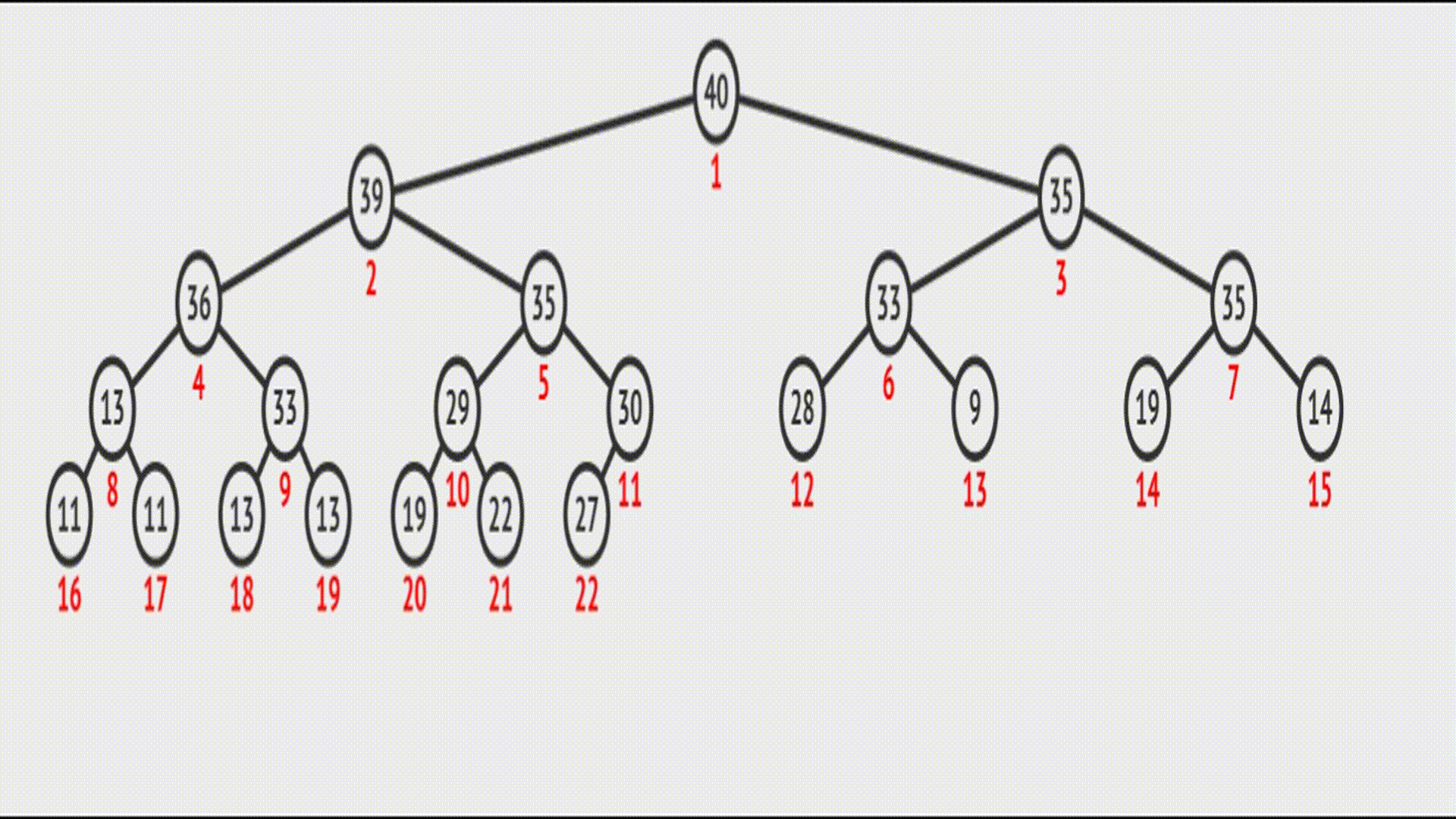 在
在vector中的效果(实际效果):
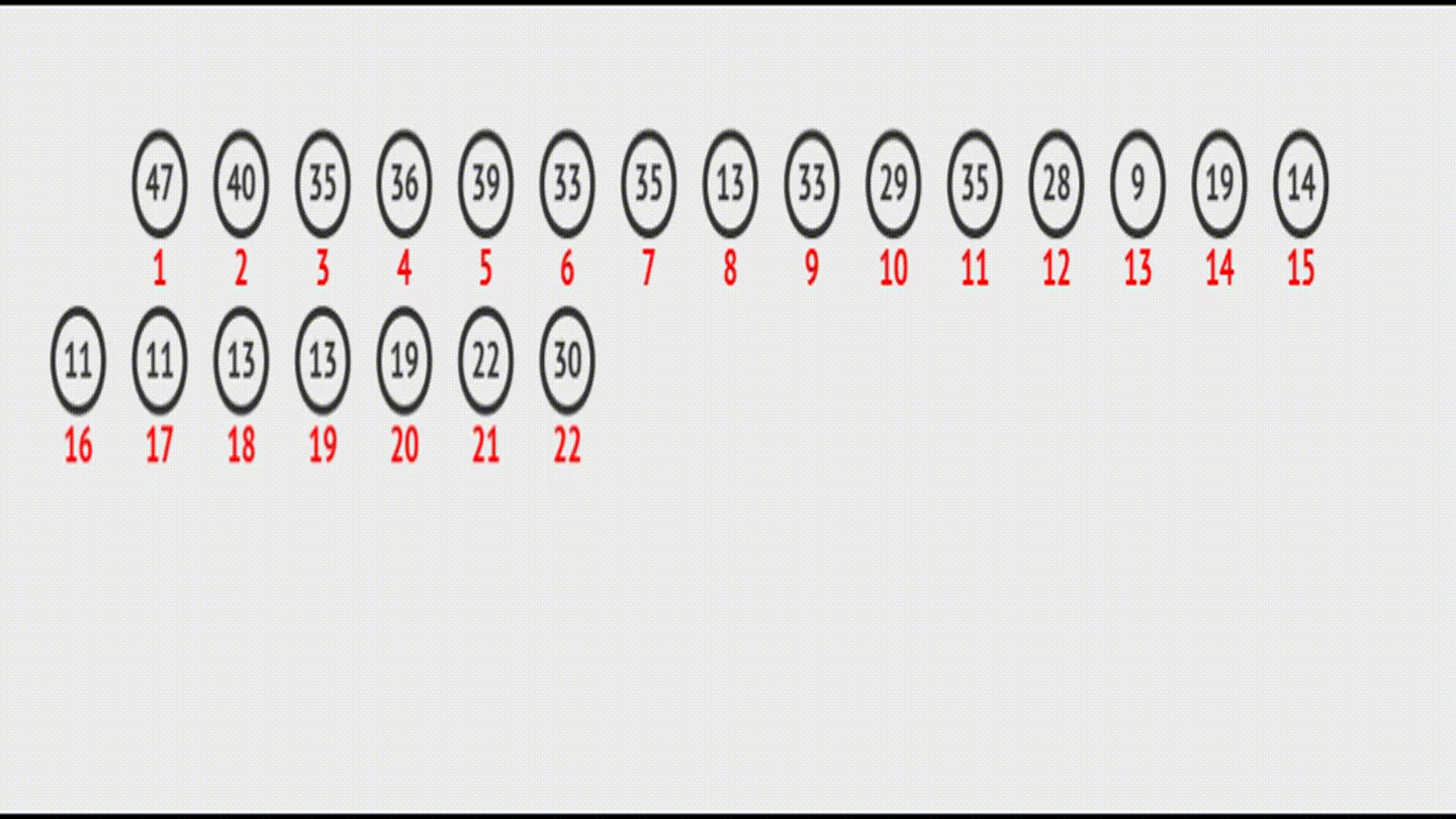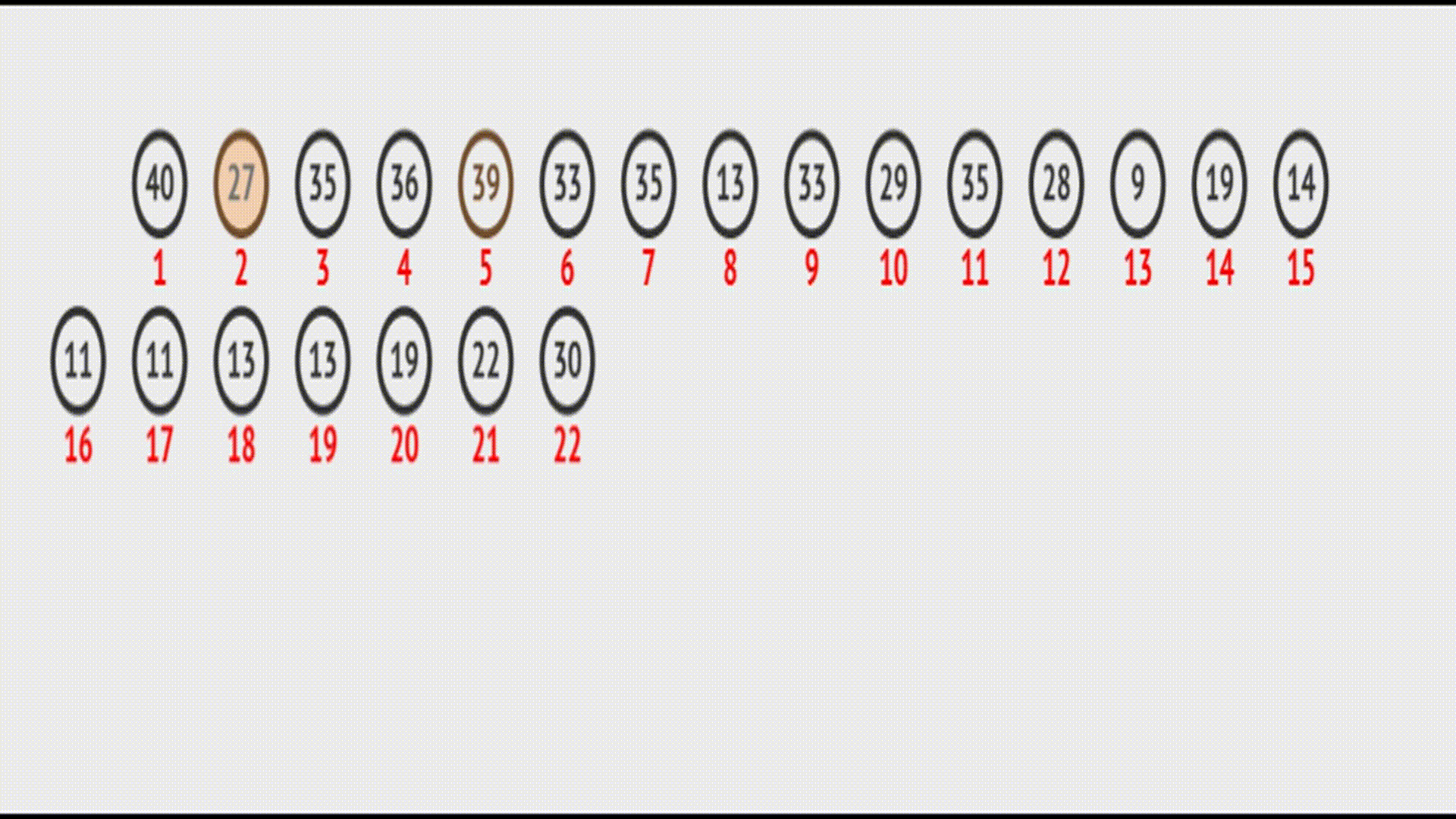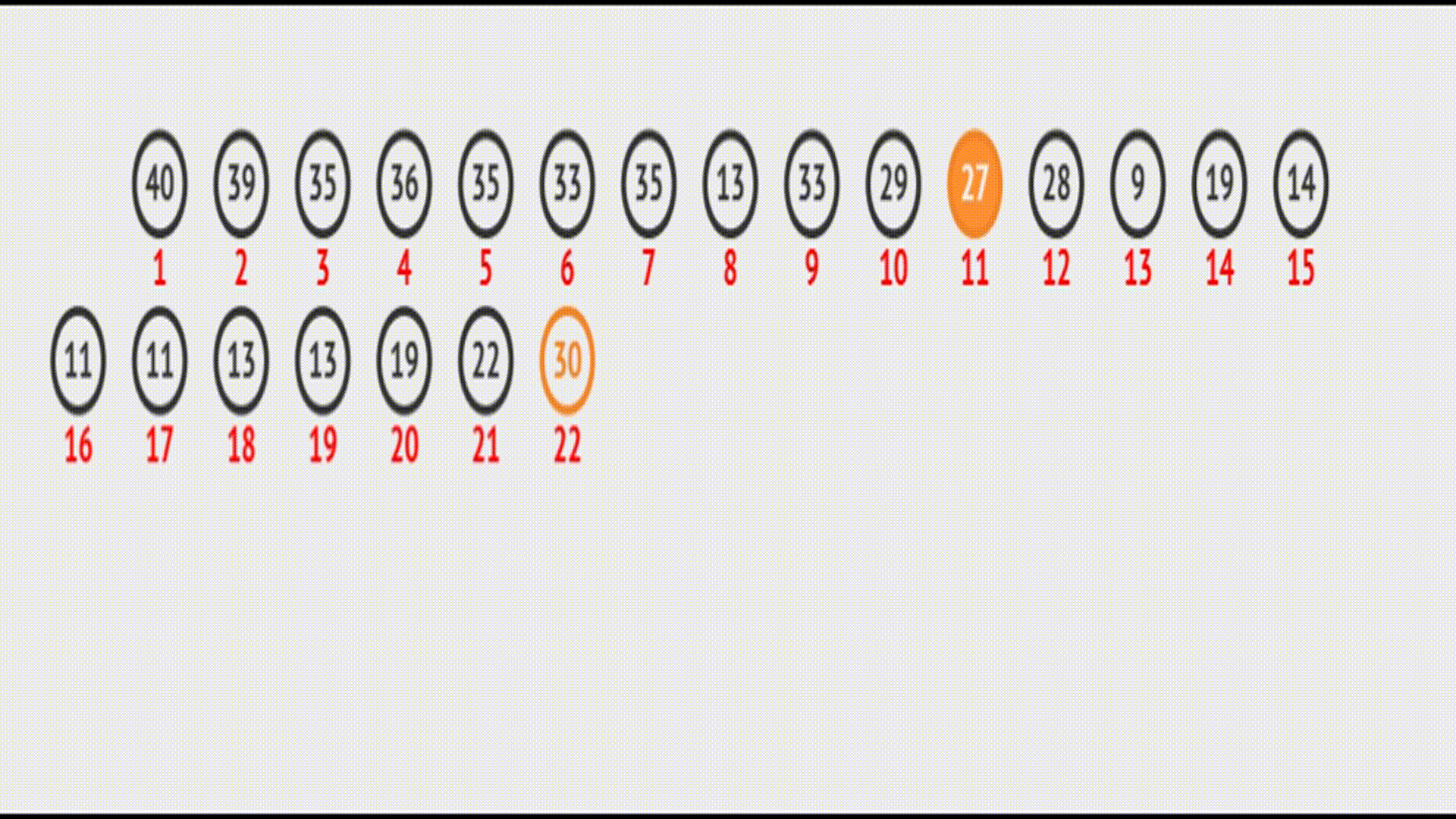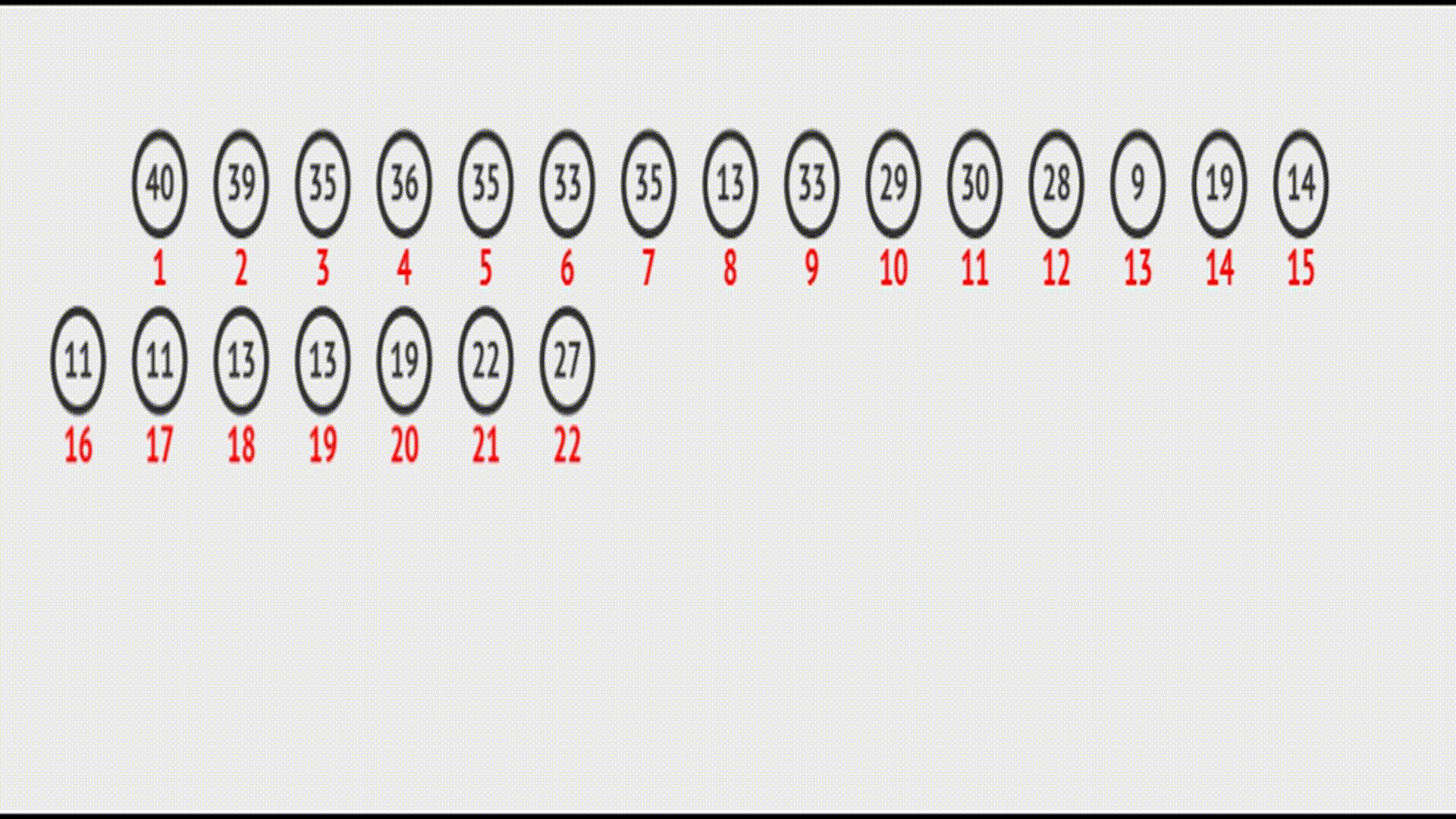
代码如下:
void AdjustDown(int parent)
{
int child = parent * 2 + 1;
while (child < _con.size())
{
if (child + 1 < con.size() && _con[child + 1] > _con[child])
{
child++;
}
if (_con[child] > _con[parent])
{
Swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
首先,计算待调整节点的左子节点下标child = parent * 2 + 1。
然后,进入一个循环,判断child是否越界。如果child < size,则说明待调整节点有左子节点。
在循环中,首先判断是否存在右子节点,并且右子节点的值大于左子节点的值,如果满足这个条件,则将child更新为右子节点的下标。
接下来,判断child节点的值是否大于parent节点的值。如果满足这个条件,则交换child和parent节点的值,并更新parent为child,再次计算child的值。
如果child节点的值不大于parent节点的值,则退出循环。
函数结束后,即可保证以parent节点为根的子树满足堆的性质。
插入与删除
push:
我们只需要将待插入元素放到末尾,然后将其向上调整即可:
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size() - 1);
}
pop:
我们只需要将第一个元素与最后一个元素交换,然后删除最后一个元素,最后把刚刚交换上来的第一个元素向下调整即可:
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
但是至此我们的优先级队列还不是完全体,因为其只能固定是大堆/小堆,或者说优先级的比较方式是固定的,想要解决这个问题,我们就需要仿函数。
仿函数
仿函数本质上是一个类,它具有函数调用运算符(operator())的特性。仿函数的本质是一种可调用的对象,它可以像函数一样被调用。
我先为大家展示一个仿函数:
class Add
{
int operator()(int a, int b)
{
return a + b;
}
};
int main()
{
Add add;
int result = add(3, 4);
return 0;
}
在上面的示例中,我们定义了一个名为Add的类,它重载了函数调用运算符operator(),并实现了对两个整数相加的逻辑。在主函数中,我们创建了一个Add的实例add,并通过调用函数调用运算符对两个整数进行相加。
add本质上明明是一个类的对象,但是由于重载了运算符operator(),所以可以模仿函数的行为,完成函数的调用。
那么我们为什么不直接写一个函数,完成两个数字的加法,而是要搞仿函数这样的东西呢?
这就不得不提到被人诟病的C语言函数指针体系了,在C语言中,如果我们想将一个函数作为参数传给其他函数,那么我们就要在形参列表中准确写出函数指针的类型。但是函数指针经常会非常复杂,用起来很难受。
但是对象就不一样了,如果我们将仿函数的对象作为参数传递,此时的类型就非常好写了。
其次是内联函数的问题:
仿函数是定义在类中的,类中的成员函数默认为内联函数,此时短小的函数就会被展开。而如果是一般的函数,用inline修饰后,由于要在指定位置展开,此时就没有地址,没有函数指针了,所以内联函数无法作为参数传递。如果inline修饰的函数被作为函数指针传递,此时这个函数的inline就会失效,从而无法展开。而仿函数很好解决了这个问题
所以仿函数有两大优点:
- 避免了复杂的函数指针体系,我们可以很方便的将仿函数作为参数传递
- 仿函数可以作为参数传递的同时,还支持内联函数
对于我们的优先级队列,我们就可以使用仿函数作为一个模板参数。
用户使用优先级队列时,可以自己传入一个仿函数,从而制定自己的规则,按照自己设想的方法来排列数据。
比大小的仿函数:
template <class T>
struct less
{
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
template <class T>
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
完整版priority_queue:
template <class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
void adjust_up(int x)
{
int child = x;
int parent = (child - 1) / 2;
while (child > 0)
{
if (Compare()(_con[parent], _con[child]))
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void adjust_down(int x)
{
int parent = x;
int child = 2 * parent + 1;
while (child < _con.size())
{
if (child + 1 < _con.size() && Compare()(_con[child], _con[child + 1]))
{
child++;
}
if (Compare()(_con[parent], _con[child]))
{
swap(_con[child], _con[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size() - 1);
}
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
const T& top()
{
return _con[0];
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
在模板参数中,我们传入了第二个参数,用于接受一个仿函数Compare ,这个仿函数用于决定后续比较时的优先级规则。
后续我们在比较parent与child大小的地方调用了仿函数:Compare()(_con[parent], _con[child])
这里并没有多写一对括号,Compare()是一个匿名对象,而后面的(_con[parent], _con[child])则是在调用operator()。
当然,如果你认为这样可读性太差了,也可以在类中多定义一个compare类的对象cmp,后续直接cmp(_con[parent], _con[child])这样调用这个仿函数。