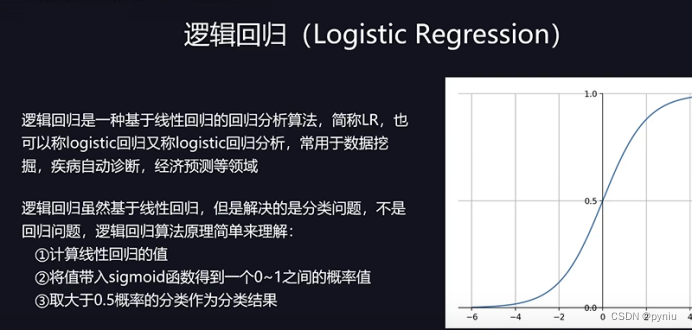


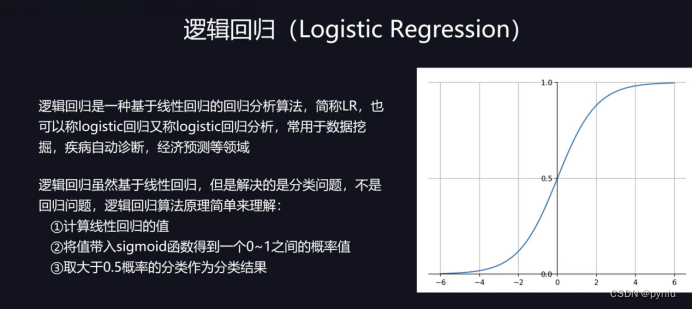
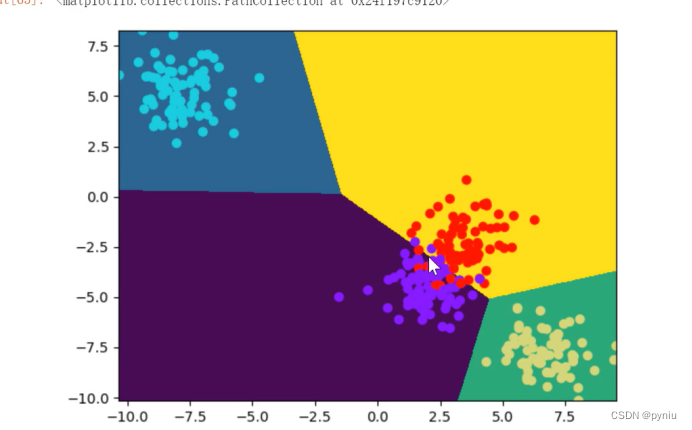
逻辑回归是基于线性回归是直线分的也可以做多分类
## 数学基础
import numpy as np
np.pi
# 三角函数
np.sin()
np.cos()
np.tan()
# 指数
y=3**x
# 对数
np.log10(10)
np.log2(2)
np.e
np.log(np.e) #ln(e)
# 对数运算
# log(AB) = log(A) + logB
np.log(3*4)==np.log(3)+np.log(4)
# logA² = 2 * logA
np.log(3**4)==4*np.log(3)
导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)
矩阵: 在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合
**方阵**: 行数、列数相等的矩阵
阶: 方阵的行数或列数
import numpy as np
n=np.array([[1,2,9],[2,3,4]])
n
#### 矩阵求逆
# np.linalg: linear algebra 线性代数
# 求逆
np.linalg.inv(n)
# 行列式的值
np.linalg.det(n)
np.round(np.linalg.det(n)) #np.round()是NumPy库中的一个函数,用于对数组或单个数值进行四舍五入
**单位矩阵**
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。根据单位矩阵的特点,任何矩阵与单位矩阵相乘都等于本身
矩阵积
np.dot(n2, n)
单位矩阵符合交换律: 任何矩阵与单位矩阵相乘都等于本身
I是单位矩阵
I.A = A.I = A
n1 = np.array([[1, 2, 3], [2, 3, 4]])
n2 = np.array([[1, 2, 3], [2, 3, 4], [3, 4, 5]])
display(n1,n2)
np.dot(n1,n2)
# 求n的逆
n_inv=np.linalg.inv(n)
n_inv
#### 矩阵的秩 (了解)
定义: 在m * n矩阵A中, 最高阶非零子式的阶数,称为矩阵A的秩, 记作R(A)或r(A)
linalg: linear algebra 线性代数
**满秩矩阵(non-singular matrix)**: 设A是n阶矩阵, 若r(A) = n, 则称A为满秩矩阵。但满秩不局限于n阶矩阵。若矩阵秩等于行数,称为行满秩;若矩阵秩等于列数,称为列满秩。既是行满秩又是列满秩则为n阶矩阵即n阶方阵。如果是方阵,行满秩矩阵与列满秩矩阵是等价的。
满秩有行满秩和列满秩,既是行满秩又是列满秩的话就一定是是方阵
**奇异矩阵** 是线性代数的概念,就是该矩阵的秩不是满秩。首先,看这个矩阵是不是方阵(即行数和列数相等的矩阵。若行数和列数不相等,那就谈不上奇异矩阵和非奇异矩阵)