原题链接:https://atcoder.jp/contests/abc340/tasks/abc340_c
Time Limit: 2 sec / Memory Limit: 1024 MB
Score: 300 points
问题陈述
黑板上写着一个整数 N。
高桥将重复下面的一系列操作,直到所有不小于2的整数都从黑板上移除:
- 选择写在黑板上的一个不小于2的整数x。
- 擦去黑板上出现的一个x。然后,在黑板上写下两个新的整数 ⌊x/2⌋ 和 ⌈x/2⌉。
- 高桥必须支付 x 日元才能完成这一系列操作。
这里,⌊a⌋表示不大于a的最大整数,⌈a⌉表示不小于a的最小整数。
当不能再进行操作时,高桥支付的总金额是多少?
可以证明,无论操作的顺序如何,他支付的总金额是不变的。
Constraints
- 2≤N≤10^17
Sample Input 1Copy
3
Sample Output 1Copy
5
样本输出 1
下面是高桥如何执行操作的示例:
- 最初,黑板上写着一个 3。
- 他选择了 3。他支付了3日元,擦去了黑板上的一个3,并在黑板上写下了⌊3/2⌋=1和⌈3/2⌉=2
- 黑板上写着一个2和一个1。
- 他选择了2。他支付了2日元,擦去了黑板上的一个2,并在黑板上写下了⌊2/2⌋=1和⌈2/2⌉=1
- 黑板上写了三个1。
- 由于所有不小于2的整数都已从黑板上擦除,因此过程结束。
高桥为整个过程总共支付了3+2=5日元,因此打印5。
Sample Input 2Copy
340
Sample Output 2Copy
2888
Sample Input 3Copy
100000000000000000
Sample Output 3Copy
5655884811924144128
解题思路:
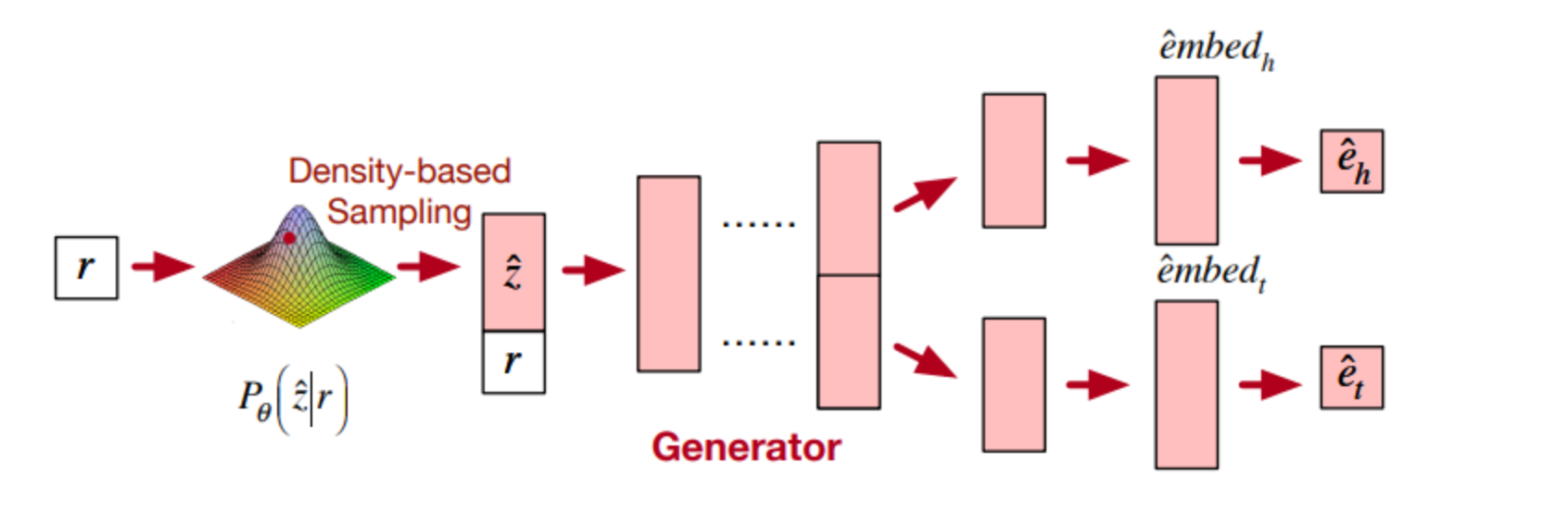
首先这个题目n非常大,肯定不能暴力,像这种题要么就是有什么规律,要么就是可以打表直接推出计算公式的,这个题目我当时是打表然后直接推出了计算公式做出来的,这个题目不难,但是我觉得有点意思,所以这里来说一下我的思路,我看了榜上有很多D,E都做出来了但是这个题目没做出来的,D纯纯最短路模板题,然后E区间维护(树状数组,线段树)模板题,没什么意思,这个C比D,E有意思多了,下面我贴一个我打表的图:

第一个图n=10,下面红色框框里面的每一行的和都是10,其他的图也是如此,这里我只列举了几个数据,那么对于任意的n的红色框框中会有几行呢,多打表几个数据会发现,n有几个因子2,那么就会有几行,那么这一部分的计算方式就是n*(row),row表示n的因子2的个数,那么对于红色框框的下面这一部分(也就是最后一行)怎么计算呢,我们可以知道的是最后一行有一部分1和一部分2,根据题意1属于无效数据,所以我们只需要关心最后一行有多少个2即可,实际上下面还有一行全是1,只是1是无效数据,这一行我就没列举出来了,最后一行的2实际上就是在一部分1上面加1,由于n的所有因子2在上面红色框操作结束之后到最后一行都会变成1,在最后一行1上面加1,实际上就是n除去所有因子2之后的余数,假设n有k个因子2,那么余数r=n-(2^k),那么这一部分会让r个1变为2,会有r*2的贡献,这一部分的计算方式就是r*2,那么总的计算公式就是n*row+r*2。
时间复杂度:计算n有多少个因子2,时间为O(logn)。
空间复杂度:O(1)。
cpp代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n;
int main()
{
cin >> n;
LL v = 2;
LL ans = 0;
while (v <= n)
{
ans += n; //有多少个因子2就加多少个n
v *= 2;
}
v /= 2; //上面求出来的是大于n的最小的2的幂,这里除以2就是小于等于n的最大的2的幂
ans += 2ll * (n - v); //n-v就是余数了
cout << ans << endl;
return 0;
}