2.13学习总结

news2024/11/30 4:55:42

1.出差（Bleeman—ford）（spfa）
（dijkstra）
2.最小生成树（prim）（Kruskal）

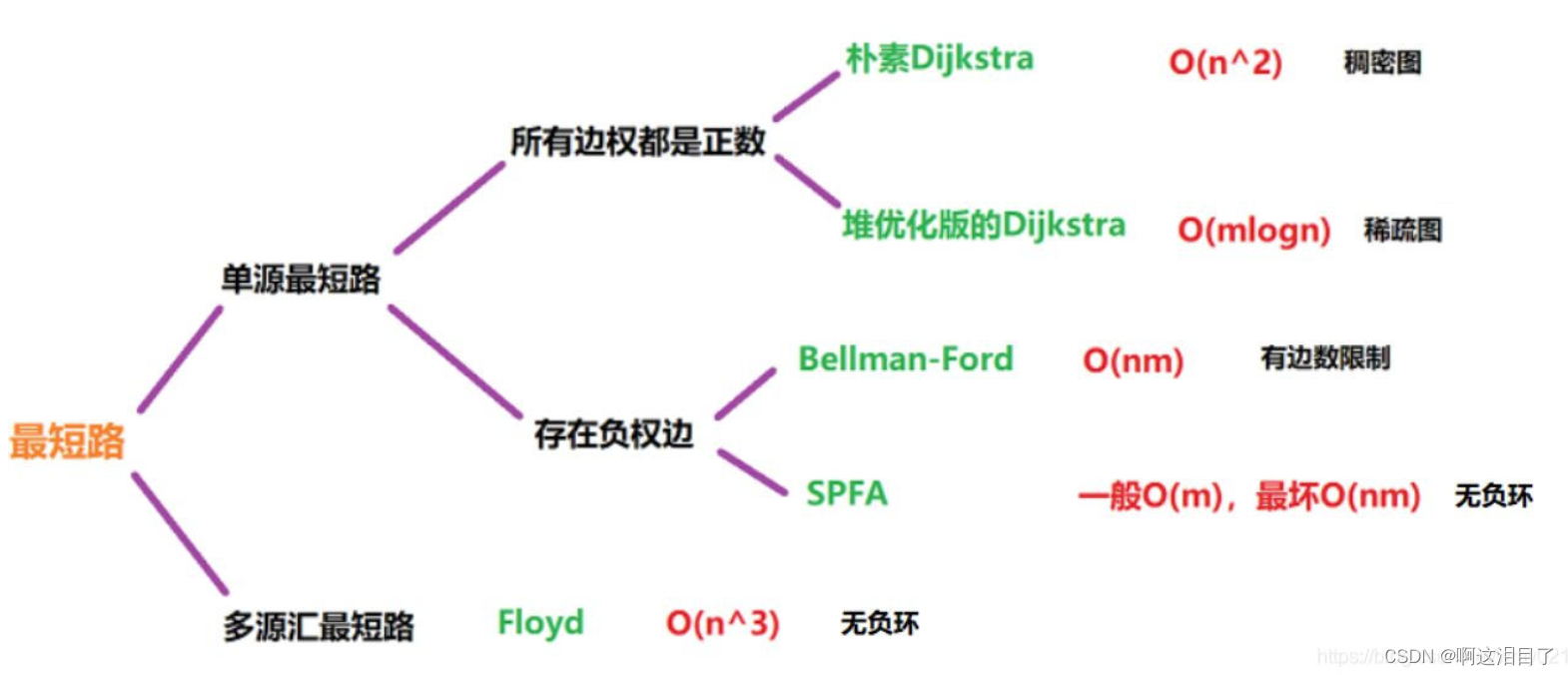
最短路问题：

出差https://www.luogu.com.cn/problem/P8802

题目描述

AA 国有 �N 个城市，编号为 1…�1…N 小明是编号为 11 的城市中一家公司的员工，今天突然接到了上级通知需要去编号为 �N 的城市出差。

由于疫情原因，很多直达的交通方式暂时关闭，小明无法乘坐飞机直接从城市 11 到达城市 �N，需要通过其他城市进行陆路交通中转。小明通过交通信息网，查询到了 �M 条城市之间仍然还开通的路线信息以及每一条路线需要花费的时间。

同样由于疫情原因，小明到达一个城市后需要隔离观察一段时间才能离开该城市前往其他城市。通过网络，小明也查询到了各个城市的隔离信息。（由于小明之前在城市 11，因此可以直接离开城市 11，不需要隔离）

由于上级要求，小明希望能够尽快赶到城市 NN, 因此他求助于你，希望你能帮他规划一条路线，能够在最短时间内到达城市 �N 。

输入格式

第 11 行：两个正整数 �,�N,M 表示 A 国的城市数量, �M 表示末关闭的路线数量。

第 22 行: �N 个正整数，第 �i 个整数 ��Ci​ 表示到达编号为 ii 的城市后需要隔离的时间。

第 3…�+23…M+2 行: 每行 33 个正整数, �,�,�u,v,c, 表示有一条城市 �u 到城市 �v 的双向路线仍然开通着，通过该路线的时间为 �c。

输出格式

第 11 行：11 个正整数，表示小明从城市 11 出发到达城市 �N 的最短时间。（到达城市 �N，不需要计算城市 �N 的隔离时间）

输入输出样例

输入 #1复制

4 4
5 7 3 4
1 2 4
1 3 5
2 4 3
3 4 5

输出 #1复制

13

说明/提示

【样例说明】

【评测用例规模与约定】

对于 100%100% 的数据, 1≤�≤1000,1≤�≤10000,1≤��≤200,1≤�,�≤1≤N≤1000,1≤M≤10000,1≤Ci​≤200,1≤u,v≤ �,1≤�≤1000N,1≤c≤1000

Dijkstra算法：

主要是利用邻接表和优先队列实现，总复杂度是O（nlongn）

实现：起点先入队，然后找到所有的邻居入队（除了已经标记了找到最短路的），找后序点的时候，优先选择路径短的点（用优先队列实现）

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f
const int N=20010;
int n,m;
int t[N],dist[N];
struct edge{
	int to;
	int w;
	edge(int a,int b) {
		to=a;
		w=b;
	}	
};
vector<edge>e[N];
struct node{
	int id;
	int n_dis;
	node(int aa,int bb){
		id=aa;
		n_dis=bb;
	}
	bool operator < (const node& a)const{
		return n_dis > a.n_dis;
	}
};
void dijkstra(){
	bool done[N];	//标记数组，用于确定是否该节点找到最短路径 
	for (int i=1;i<=n;++i){
		done[i]=false;
		dist[i]=INF;
	}
	dist[1]=0;	//初始化，起点到起点的距离为0 
	priority_queue<node>q;
	q.push(node(1,dist[1]));
	while (!q.empty()){
		node p=q.top(); q.pop();
		if (done[p.id]) continue;
		done[p.id]=true;
		for (int i=0;i<e[p.id].size();++i){
			int y=e[p.id][i].to;
			int w=e[p.id][i].w;
			if (done[y]) continue;
			int res=t[y];
			if (y==n) res=0;
			if (dist[y]> p.n_dis+w+res){	//当前节点y到起点的最短路径大于路过p点到y点的路径 
				dist[y]=p.n_dis+w+res;
				q.push(node(y,dist[y]));
			}
		}
	}
}
signed main(){
	cin>>n>>m;
	for (int i=1;i<=n;++i) cin>>t[i];
	for (int i=0;i<m;++i){	//建立邻接表 
		int a,b,c;
		cin>>a>>b>>c;
		e[a].push_back(edge(b,c));
		e[b].push_back(edge(a,c));
	}
	dijkstra();
	cout<<dist[n];
}

Bleeman—ford算法：

复杂度的是O（n^2），相比与floyd算法，该算法主要是找相邻节点,每一轮操作会找到一个最短路径的点，由于有n个点，所以需要进行n次，然后每次需要遍历所有的边。

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
int INF=0x3f3f3f3f;
const int N=20010;
int t[N],dist[N];
struct edge{
	int a;
	int b;
	int c;
}e[N];
signed main(){
	int n,m;
	cin>>n>>m;
	for (int i=1;i<=n;++i) cin>>t[i];
	for (int i=0;i<m;++i){
		int a,b,c;
		cin>>a>>b>>c;
		e[i].a=a,e[i].b=b,e[i].c=c;
		e[i+m].a=b,e[i+m].b=a,e[i+m].c=c;
	}
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	for (int k=1;k<=n;++k){	
		for (int i=0;i<2*m;++i){	//双向的 
			int u=e[i].a,v=e[i].b;
			int res=t[v];
			if (v==n)res=0;
			dist[v]=min(dist[v],dist[u]+res+e[i].c);	
		}
	}
	cout<<dist[n];
}

SPFA算法：算法复杂度和Dijkstra一样，但是在最坏的情况下会达到O（n^2）是Bleeman—ford的优化，只更新上一轮有变化的点，不更新所有的点

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f
const int N=20010;
int n,m;
int t[N],dist[N];
struct edge{
	int to;
	int w;
	edge(int a,int b) {
		to=a;
		w=b;
	}	
};
vector<edge>e[N];
int inq[N];	//判断是否在队列内 
void spfa(){
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	queue<int>q;	//队列内存放的是节点号 
	q.push(1);
	inq[1]=1;
	while (!q.empty()){
		int u=q.front(); q.pop();
		inq[u]=0;
		for (int i=0;i<e[u].size();++i){
			int v=e[u][i].to;
			int w=e[u][i].w;
			int res=t[v];
			if (v==n) res=0;
			if (dist[v]>res+dist[u]+w){		//只处理更新的节点 
				dist[v] =dist[u]+w+res;
				if (!inq[v]){
				inq[v]=1;
				q.push(v);
				}
			}
		}
	}
}
signed main(){
	cin>>n>>m;
	for (int i=1;i<=n;++i) cin>>t[i];
	for (int i=0;i<m;++i){
		int a,b,c;
		cin>>a>>b>>c;
		e[a].push_back(edge(b,c));
		e[b].push_back(edge(a,c));
	}
	spfa();
	cout<<dist[n];
}

最小生成树：

最小生成树https://www.luogu.com.cn/problem/P3366

题目描述

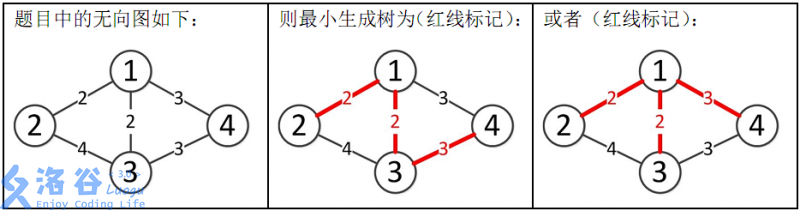
如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 �,�N,M，表示该图共有 �N 个结点和 �M 条无向边。

接下来 �M 行每行包含三个整数 ��,��,��Xi​,Yi​,Zi​，表示有一条长度为 ��Zi​ 的无向边连接结点 ��,��Xi​,Yi​。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

输入输出样例

输入 #1复制

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出 #1复制

7

说明/提示

数据规模：

对于 20%20% 的数据，�≤5N≤5，�≤20M≤20。

对于 40%40% 的数据，�≤50N≤50，�≤2500M≤2500。

对于 70%70% 的数据，�≤500N≤500，�≤104M≤104。

对于 100%100% 的数据：1≤�≤50001≤N≤5000，1≤�≤2×1051≤M≤2×105，1≤��≤1041≤Zi​≤104。

样例解释：

所以最小生成树的总边权为 2+2+3=72+2+3=7。

Prim算法和Kruskal算法的异同

同：都是利用贪心的方式

异：

Prim算法原理：“最小的邻居一定在树上”，从任意一个点u开始，把距离最近的v加入最小生成树中，下一步把距离{u，v}最近的w加入到树中，并且在生成的过程中保证不会生成环路，直到所有的点都在树上

代码与Dijkstra类似

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f

const int N=4e5+5;
struct edge{
	int to;
	int w;
	edge(int a,int b){
		to=a;
		w=b;
	}
};
vector<edge>e[N];
int n,m,ans;
struct node{
	int id;
	int n_dis;	//区别在于Dijkstra这里存的是该节点到起点的最短距离，而Prim中存的是边长(该节点与其他邻居节点的最短边长) 
	node(int a,int b): id(a),n_dis(b){}
	bool operator < (const node &a)const{
		return n_dis>a.n_dis;
	}
};
priority_queue<node>q;
bool done[N];
int dis[N];
void prim(){
	for (int i=1;i<=n;++i){
		done[i]=false;
		dis[i]=INF;
	}
	dis[1]=0;
	q.push(node(1,dis[1]));
	while (!q.empty()){
		node p=q.top(); q.pop();
		if (done[p.id]) continue;
		done[p.id]=true;
		ans+=dis[p.id];
		for (int i=0;i<e[p.id].size();++i){
			int  v=e[p.id][i].to;
			int  w=e[p.id][i].w;
			if (done[v]) continue;
			if (dis[v]> w){
				dis[v]=w;
				q.push(node(v,w));
			}
		}
	}
	for (int i=1;i<=n;++i){
		if (!done[i]){
			cout<<"orz";
			return;
		}
	}
	cout<<ans;
	return ;
}


signed main(){
	cin>>n>>m;
	for (int i=0;i<m;++i){
		int a,b,c;
		cin>>a>>b>>c;
		e[a].push_back(edge(b,c));
		e[b].push_back(edge(a,c));
	}
	prim();
}

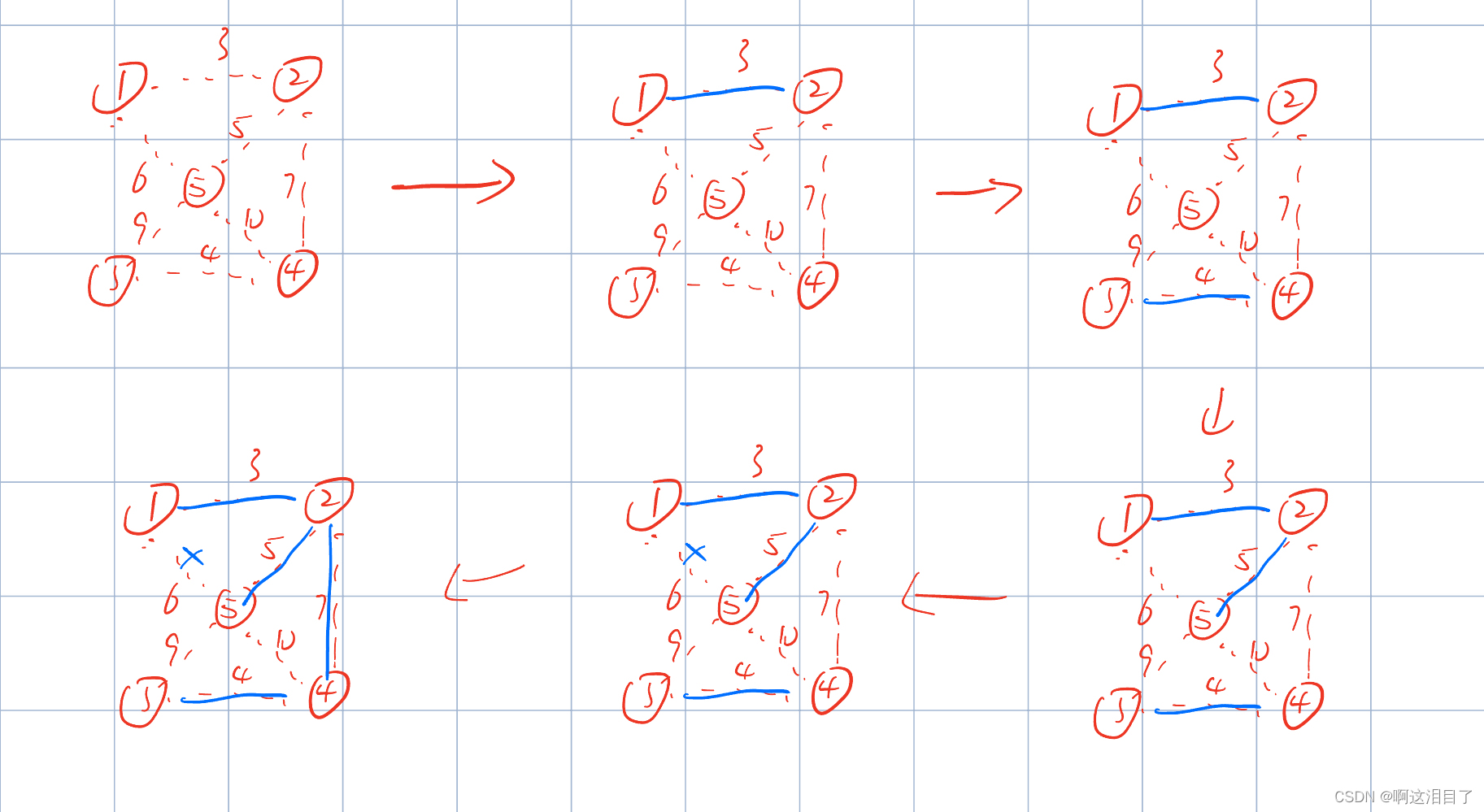
Kruskal算法原理：

“最短的边一定在最小生成树上”，从最短的边开始操作，以此加到树中。

算法步骤：先对所有的节点关系进行排序，然后依次把最小的边放到最小生成树中，其中对于是否成环（连通性问题）的判定，可以用并查集实现

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f

const int N=4e5+5;
int f[N]; 
struct edge{
	int from;
	int to;
	int dis;
};
edge e[N];
bool cmp(const edge& a,const edge& b){
	return a.dis<b.dis;
}
int find(int x){
	if (f[x]==x){
		return x;
	}else {
		f[x]=find(f[x]);
		return f[x];
	}
}
void unionn(int i,int j){
	f[find(i)]=find(j);
}
int n,m,ans,cnt;

void Kruskal(){
	for (int i=1;i<=n;++i){
		f[i]=i;
	}
	sort(e+1,e+1+m,cmp);	//排序 
	for (int i=1;i<=m;++i){	//开始放边 
		if (find(e[i].from)!=find(e[i].to)){	//如果不会构成环 
			cnt++;	//节点就放到树上 
			ans+=e[i].dis;
			unionn(find(e[i].from),find(e[i].to));	//合并两个节点 
		}
		if (cnt==n-1)break;
	}
	if (cnt!=n-1) cout<<"orz";
	else if (cnt==n-1) cout<<ans;
}
signed main(){
	cin>>n>>m;
	for (int i=1;i<=m;++i){
		cin>>e[i].from>>e[i].to>>e[i].dis;
	}
	Kruskal();
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1447713.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

专利申请与论文发表有什么区别

专利申请与论文发表有什么区别

一、背景 专利申请和发表期刊论文是科研成果两种不同的保护与传播方式&#xff0c;它们的主要区别在于&#xff1a; 1. 目的与性质&#xff1a; - **专利申请**&#xff1a;主要目的是获得对发明创造的法律保护&#xff0c;确保发明人在一定时期内&#xff08;如发明专利通…
阅读更多...
数据工程工程师学习路线图

数据工程工程师学习路线图

数据工程岗位要求 Skill Sets required: - Hands on experience enabling data via Adobe Analytics and/or Google Analytics - Understanding of how customer level data is captured and stitched with behavioural data - Experience working with Testing (QA) and D…
阅读更多...
复旦大学最新研究：如何让大模型敢回答“我不知道”？

复旦大学最新研究：如何让大模型敢回答“我不知道”？

引言&#xff1a;AI助手的真实性挑战 在人工智能&#xff08;AI&#xff09;的发展进程中&#xff0c;基于大型语言模型&#xff08;LLMs&#xff09;的AI助手已经在多个任务中展现出惊人的性能&#xff0c;例如对话、解决数学问题、编写代码以及使用工具。这些模型拥有丰富的…
阅读更多...
【设计模式】springboot3项目整合模板方法深入理解设计模式之模板方法（Template Method）

【设计模式】springboot3项目整合模板方法深入理解设计模式之模板方法（Template Method）

&#x1f389;&#x1f389;欢迎光临&#x1f389;&#x1f389; &#x1f3c5;我是苏泽&#xff0c;一位对技术充满热情的探索者和分享者。&#x1f680;&#x1f680; &#x1f31f;特别推荐给大家我的最新专栏《Spring 狂野之旅&#xff1a;底层原理高级进阶》 &#x1f680…
阅读更多...
C#使用密封类密封用户信息

C#使用密封类密封用户信息

目录 一、涉及到的知识点 1.密封类定义 2.何时使用密封类 3.使用密封类的注意事项 二、实例1 三、实例2 1.源码 2.生成效果 在C#中&#xff0c;密封类&#xff08;sealed class&#xff09;是一种不能被其他类继承的类。它用于防止其他类继承它的功能和属性。 一、涉…
阅读更多...
键盘重映射禁用 CtrlAltDel 键的利弊

键盘重映射禁用 CtrlAltDel 键的利弊

目录 前言 一、Scancode Map 的规范 二、禁用 CtrlAltDel 的方法及其缺陷 三、编程实现和测试 3.1 C 实现的简易修改工具 3.2 C# 实现的窗口工具 四、总结 本文属于原创文章&#xff0c;转载请注明出处&#xff1a; https://blog.csdn.net/qq_59075481/article/details…
阅读更多...
如何才能学好JVM？——零基础入门篇

如何才能学好JVM？——零基础入门篇

1. JVM是什么&#xff1f; JVM是Java Virtual Machine的简称&#xff0c;它是一个虚拟的计算机&#xff0c;专门为执行Java程序而设计。 你可以想象它是一个能够运行Java字节码的平台&#xff0c;无论你的程序在Windows、Mac还是Linux上&#xff0c;它们都能通过JVM在这些系统…
阅读更多...
单调队列优化DP问题

单调队列优化DP问题

目录 1.滑动窗口 2.最大子序和 3.旅行问题 4.烽火传递 5.绿色通道 6.修剪草坪 7.理想的正方形 1.滑动窗口 154.给定一个大小为 n≤106 的数组。 有一个大小为 k 的滑动窗口&#xff0c;它从数组的最左边移动到最右边。 你只能在窗口中看到 k 个数字。 每次滑动窗口向…
阅读更多...
RBF神经网络中的RBF的英文全称是什么，是用来干什么的？

RBF神经网络中的RBF的英文全称是什么，是用来干什么的？

问题描述&#xff1a;RBF神经网络中的RBF的英文全称是什么&#xff0c;是用来干什么的&#xff1f; 问题解答&#xff1a; RBF神经网络中的RBF是径向基函数&#xff08;Radial Basis Function&#xff09;的缩写。径向基函数是一种在机器学习和模式识别中常用的函数类型&…
阅读更多...
Peter算法小课堂—区间模型

Peter算法小课堂—区间模型

Peter Pan来啦…… 最大不重叠区间数 二话不说&#xff0c;先来一道题 大家想想怎么贪心&#xff1f;我们可以将每一个美食摊位抽象成一个区间&#xff0c;区间左端点为开始排队时间&#xff0c;右端点为结束排队时间。其中&#xff0c;时间信息可以用数轴表示。 额……我们…
阅读更多...
【Spring MVC篇】Cookie和Session的获取 Header的获取

【Spring MVC篇】Cookie和Session的获取 Header的获取

个人主页&#xff1a;兜里有颗棉花糖 欢迎 点赞&#x1f44d; 收藏✨ 留言✉ 加关注&#x1f493;本文由 兜里有颗棉花糖 原创 收录于专栏【Spring MVC】 本专栏旨在分享学习Spring MVC的一点学习心得&#xff0c;欢迎大家在评论区交流讨论&#x1f48c; Cookie是客户端保存用…
阅读更多...
【知识整理】产研中心岗位评定标准之测试岗位

【知识整理】产研中心岗位评定标准之测试岗位

为贯彻执行集团数字化转型的需要,该知识库将公示集团组织内各产研团队不同角色成员的职务“职级”岗位的评定标准; 一、定级定档目的 通过对公司现有岗位及相应岗位员工的工作能力、工作水平进行客观公正评定,确定各岗位的等级及同等级岗位员工对应的档级,从而为员工以后的晋升…
阅读更多...
M3芯片支持追光效果吗？苹果电脑上值得玩的游戏大作有什么？ Mac电脑热门游戏推荐 苹果电脑玩幻兽帕鲁 crossover软件安装

M3芯片支持追光效果吗？苹果电脑上值得玩的游戏大作有什么？ Mac电脑热门游戏推荐 苹果电脑玩幻兽帕鲁 crossover软件安装

M3是苹果最新发布的芯片&#xff0c;它采用了业界领先的3纳米工艺&#xff0c;能够提供更快的速度和更高的能效。苹果电脑是一种高端的个人电脑&#xff0c;它也有着不少优秀的游戏大作&#xff0c;能够给玩家带来不同的游戏体验。那么&#xff0c;M3支持追光效果吗&#xff1f…
阅读更多...
【AutoML】AutoKeras 进行 RNN 循环神经网络训练

【AutoML】AutoKeras 进行 RNN 循环神经网络训练

由于最近这些天都在人工审查之前的哪些问答数据&#xff0c;所以迟迟都没有更新 AutoKeras 的训练结果。现在那部分数据都已经整理好了&#xff0c;20w 的数据最后能够使用的高质量数据只剩下 2k。这 2k 的数据已经经过数据校验并且对部分问题的提问方式和答案内容进行了不改变…
阅读更多...
前端秘法引言(配置vscode, 以及html的基础)

前端秘法引言(配置vscode, 以及html的基础)

目录 一.配置环境vscode 二.配置插件 三.vscode的实用小技巧 四.标题段落换行标签 五.格式化标签 一.配置环境vscode vscode官网https://code.visualstudio.com/ 点击右上角的download 根据不同的操作系统进行下载安装,我这里选的是Windows x64 安装好后打开,点击左上角的…
阅读更多...
React官网摘抄

React官网摘抄

https://react.dev/learn 1、组件名称大写 2、变量&#xff0c;用{} vue中用{{}} react中用{}3、遍历 4、state使用
阅读更多...
Python算法题集_LRU 缓存

Python算法题集_LRU 缓存

Python算法题集_LRU 缓存 题146&#xff1a;LRU 缓存1. 示例说明2. 题目解析- 题意分解- 优化思路- 测量工具 3. 代码展开1) 标准求解【队列字典】2) 改进版一【有序字典】3) 改进版二【双向链表字典】 4. 最优算法 本文为Python算法题集之一的代码示例 题146&#xff1a;LRU …
阅读更多...
基于AI Agent探讨：安全领域下的AI应用范式

基于AI Agent探讨：安全领域下的AI应用范式

先说观点&#xff1a;关于AI应用&#xff0c;通常都会聊准召。但在安全等模糊标准的场景下&#xff0c;事实上不存在准召的定义。因此&#xff0c;AI的目标应该是尽可能的“像人”。而想要评价有多“像人”&#xff0c;就先需要将人的工作数字化。而AI Agent是能够将数字化、自…
阅读更多...
C++ //练习 6.27 编写一个函数，它的参数是initializer_list＜int＞类型的对象，函数的功能是计算列表中所有元素的和。

C++ //练习 6.27 编写一个函数，它的参数是initializer_list＜int＞类型的对象，函数的功能是计算列表中所有元素的和。

C Primer&#xff08;第5版&#xff09; 练习 6.27 练习 6.27 编写一个函数&#xff0c;它的参数是initializer_list类型的对象&#xff0c;函数的功能是计算列表中所有元素的和。 环境&#xff1a;Linux Ubuntu&#xff08;云服务器&#xff09; 工具&#xff1a;vim 代码块…
阅读更多...
现代化端口扫描工具RustScan

现代化端口扫描工具RustScan

今天是大年初五&#xff0c;喜迎财神 &#xff0c;祝大家✔️顺风顺水 ✔️诸事如意 ✔️财源滚滚 ✔️大吉大利 顺便提一下&#xff0c;老苏的博客启用了新域名&#xff1a; https://laosu.tech 什么是 RustScan &#xff1f; RustScan 是一款现代化的端口扫描器。能快速找到端…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023