力扣精选算法100道——【模板】前缀和 (二维）

news2025/1/19 7:04:59

🎈题目解析

🎈算法原理

🎈实现代码

二维前缀和【模板】

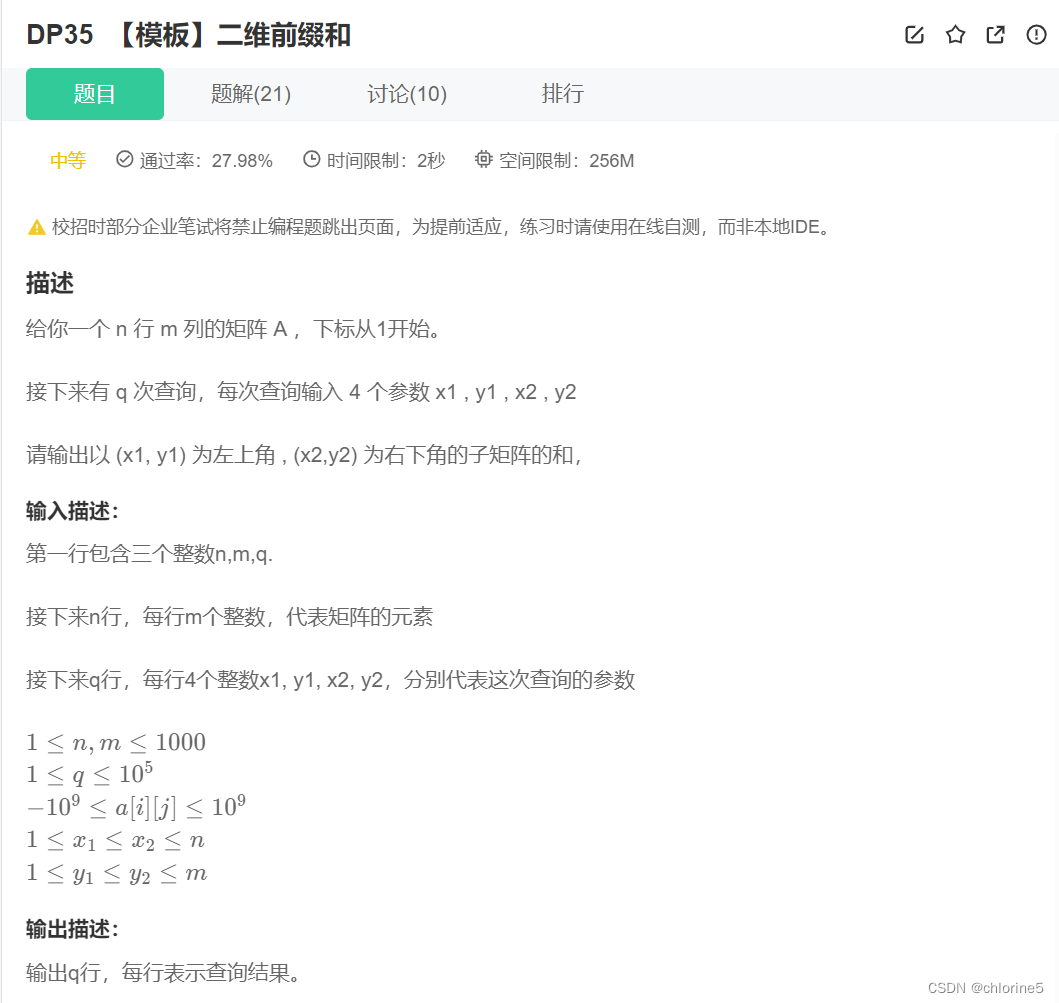
🎈题目解析

上一题我们讲述了一维的前缀和求法。

第一行三个参数，n是行数=3，m是列数=4，q=3代表查询次数

接下来就是n行m列的矩阵

剩下的q行是查询的区间，我们依次输入x1，y1, x2, y2

🎈算法原理

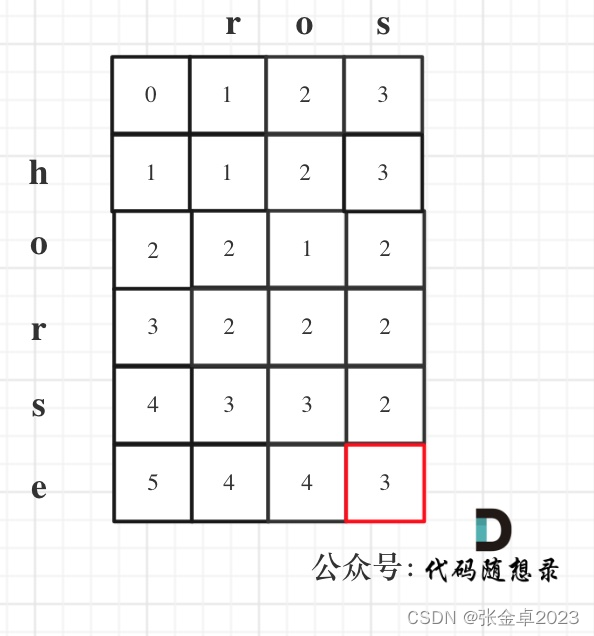
我们先想想如何计算这个正方形整个的区域和。

我们可以利用这种方法 A+B+C+D=(A+B)+(A+C)+D-A

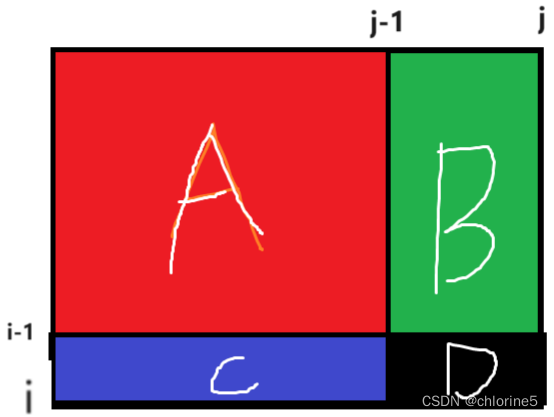
使用两层循环计算前缀和，其中 dp[i][j] 表示矩阵中从 (1,1) 到 (i,j) 的子矩阵的和。计算公式为 dp[i][j] = dp[i-1][j](A+B) + dp[i][j-1](A+C) + arr[i][j](D) - dp[i-1][j-1](A)。

dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1]。

通过循环输入查询的矩形区域的左上角和右下角坐标 (x1, y1) 和 (x2, y2)。

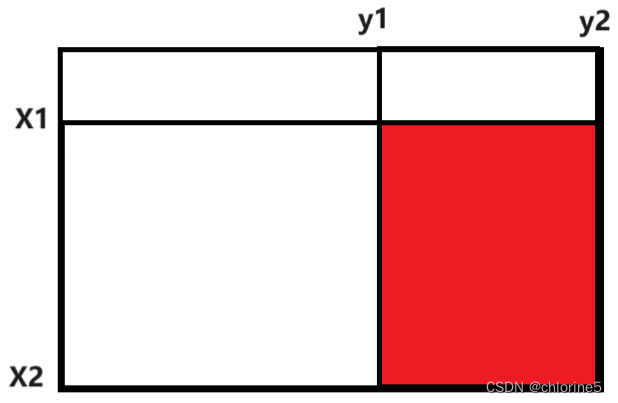
输出查询区域的和，通过使用前缀和矩阵 dp，计算出区域和为 dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]，这个公式通过前缀和的性质得出。

区域和为ret= dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]

🎈实现代码

#include <iostream>
#include<vector>
using namespace std;

int main()
{
    int n=0,m=0,q=0;
    cin>>n>>m>>q;
    vector<vector<int>>arr(n+1,vector<int>(m+1))(n*m,1);
    for (int i=1;i<=n;i++) 
    {
        for(int j=1;j<=m;j++)
        {
            cin>>arr[i][j];
        }
    }    

    //预处理前缀和公式
      vector<vector<long long>>dp(n+1,vector<long long>(m+1));
    //从(1,1)到(i,j)各个区间前缀和
      for(int i=1;i<=n;i++)
      {
        for(int j=1;j<=m;j++)
        {
            dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];
        }
      }

    //使用前缀和矩阵
    int x1=0,y1=0,x2=0,y2=0;
    while(q--)
    {
        //依次输入区间，然后计算该区域的前缀和
        cin>>x1>>y1>>x2>>y2;
        cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;
    }
    return 0;
}