完全背包

题目
文章讲解
视频讲解

完全背包和0-1背包的区别在于：物品是否可以重复使用

思路：对于完全背包问题，内层循环的遍历方式应该是从weight[i]开始一直遍历到V，而不是从V到weight[i]。这样可以确保每种物品可以被选择多次放入背包，从而求解完全背包问题。

对于完全背包问题，需要对内层循环进行调整，以确保每种物品可以被选择多次放入背包。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt(); // 研究材料种类
        int V = sc.nextInt(); // 行李箱空间

        int[] values = new int[N]; // 物品价值
        int[] weight = new int[N]; // 物品重量

        // 依次输入每种物品的重量和价值
        for (int i = 0; i < N; i++) {
            weight[i] = sc.nextInt(); // 物品重量
            values[i] = sc.nextInt(); // 物品价值
        }

        int[] dp = new int[V + 1]; // 动态规划数组
        for (int i = 0; i < N; i++) {
            for (int j = weight[i]; j <= V; j++) {
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + values[i]); // 动态规划状态转移方程
            }
        }
        System.out.println(dp[V]); // 输出结果
    }
}

一维0-1背包求解法示例如下

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt(); // 研究材料种类
        int V = sc.nextInt(); // 行李箱空间

        int[] values = new int[N]; // 物品价值
        int[] weight = new int[N]; // 物品重量

        // 依次输入每种物品的重量和价值
        for (int i = 0; i < N; i++) {
            weight[i] = sc.nextInt(); // 物品重量
            values[i] = sc.nextInt(); // 物品价值
        }

        int[] dp = new int[V + 1]; // 动态规划数组
        for (int i = 0; i < N; i++) {
            for (int j = V; j >= weight[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + values[i]); // 动态规划状态转移方程
            }
        }
        System.out.println(dp[V]); // 输出结果
    }
}

对比：

• 完全背包：
  

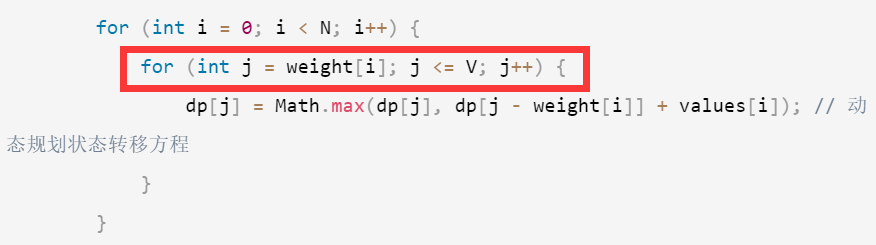
• 0-1背包：
  

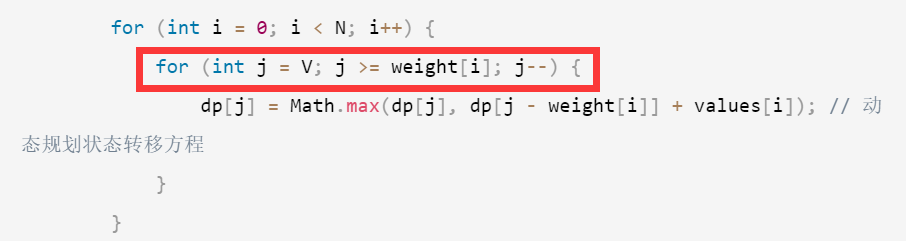
518. 零钱兑换 II

题目
文章讲解
视频讲解

思路：

1. dp[j]：凑成总金额j的货币组合数为dp[j]
2. 递推公式：dp[j] 就是所有的dp[j - coins[i]]（考虑coins[i]的情况）相加
3. 初始化需要注意 dp[0]=1;

class Solution {
    public int change(int amount, int[] coins) {

        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

377. 组合总和 Ⅳ

题目
文章讲解
视频讲解

思路：

如果求组合数就是外层for循环遍历物品，内层for遍历背包；
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

class Solution {
    public int combinationSum4(int[] nums, int target) {

        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i >= nums[j])
                    dp[i] += dp[i - nums[j]];
            }
        }
        return dp[target];

    }
}