今天主要介绍区间dp比较难的题:

下面是分析:
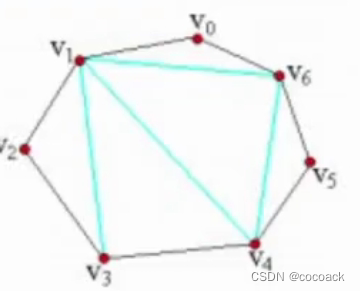 我们如果先固定点V0,那我们得去枚举两个点使它构成三角形,同时求目标值也比较难确定(起始与终止都带0),于是我们考虑固定边,我们固定v0v6然后去枚举点,这样子始终在v0--v6上剖分,不会都带0.
我们如果先固定点V0,那我们得去枚举两个点使它构成三角形,同时求目标值也比较难确定(起始与终止都带0),于是我们考虑固定边,我们固定v0v6然后去枚举点,这样子始终在v0--v6上剖分,不会都带0.
因此,我们令f[i][j]为vi--vj的最大剖分(vi与vj一定有边),目标求f[0][n];
转移方程为:f[i][j]=min(f[i][k]+f[k][j]+vi*vj*vk,f[i][j])
终止条件:f[i][i+1]=0
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
long long n,dp[60][60],a[60];
long long f(long long i,long long j){
if(j-i==1) return dp[i][j]=0;
if(dp[i][j]!=-1) return dp[i][j];
dp[i][j]=f(i,i+1)+f(i+1,j)+a[i]*a[j]*a[i+1];
for(long long k=i+2;k<=j-1;k++){
dp[i][j]=min(dp[i][j],f(i,k)+f(k,j)+a[i]*a[j]*a[k]);
}
return dp[i][j];
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
memset(dp,-1,sizeof(dp));
if(n<3) cout<<0;
else cout<<f(1,n);
}接题:
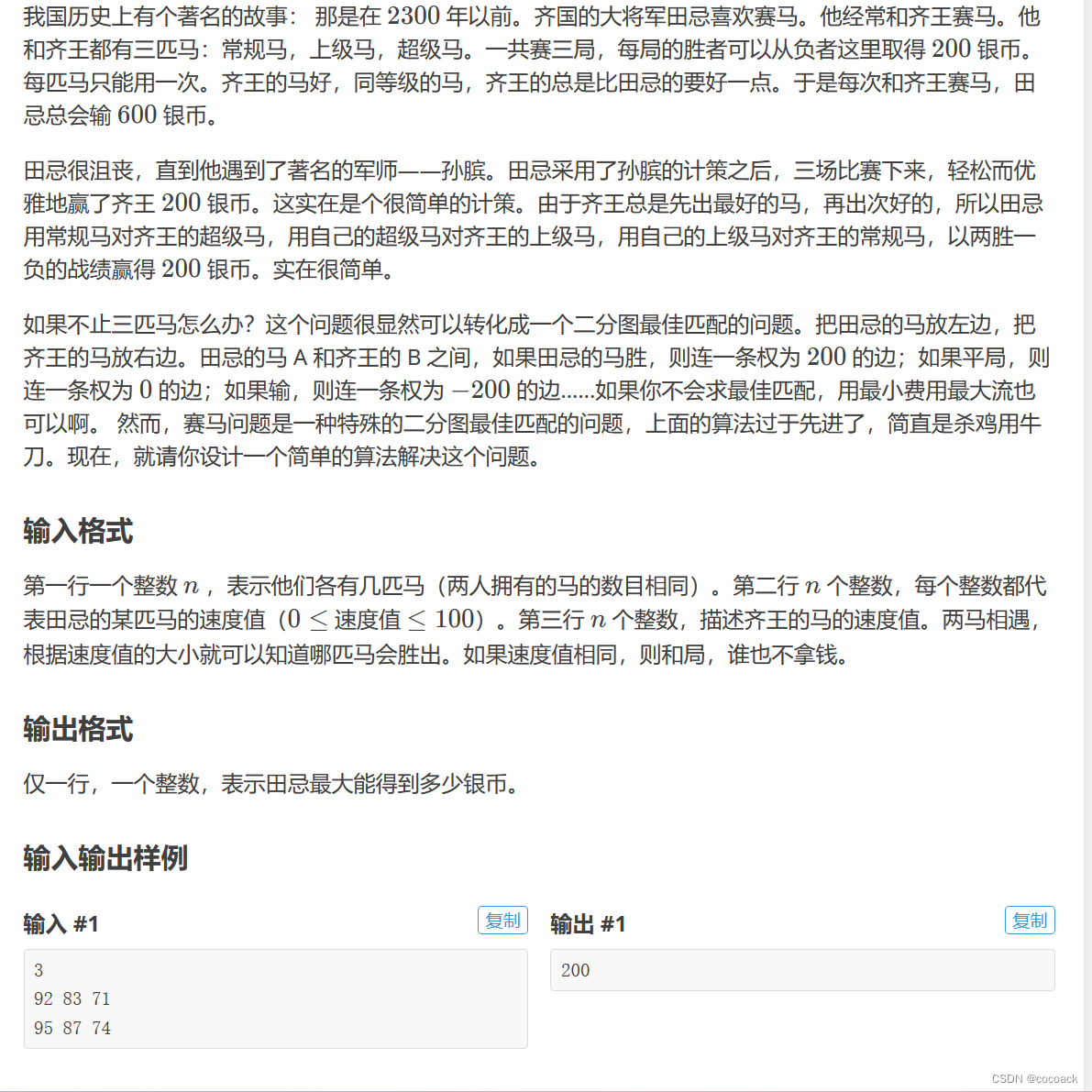
下面是分析:
显然,我们要么选最强的,要么选最弱的(如果它的马比自己所有马都强,选最弱的。
若有比他强的,选最强的,因为对手从强道弱,所以选任意一个比他强的都可以。
和最强马相等时,无法判断但一定从最强与最弱选一个,于是我们用区间dp.
每次取两个端点,中间就是连续区间,
我们令f[i][j]为某一论ai---aj的马可以赢的最大钱数。
我们发现:j-i=n-k-1;
易得转移方程为:f[i][j]=max(f[i+1][j]+a[i]与b[k],f[i][j-1]+a[j]与b[k])
这里采用记忆化搜索,如果要for的话应该从最后一轮反向开始。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,tian[2010],qi[2010],dp[2010][2010];
bool cmp(int a,int b){
return a>b;
}
int cmp1(int a,int b){
if(a>b){
return 200;
}
if(a==b){
return 0;
}
if(a<b){
return -200;
}
}
int f(int i,int j,int k){
if(i==j) return dp[i][j]=cmp1(tian[i],qi[k]);
if(dp[i][j]!=-1) return dp[i][j];
dp[i][j]=max(f(i+1,j,n+i+1-j)+cmp1(tian[i],qi[k]),f(i,j-1,n+i+1-j)+cmp1(tian[j],qi[k]));
return dp[i][j];
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) scanf("%d",&tian[i]);
for(int i=1;i<=n;i++) scanf("%d",&qi[i]);
sort(tian+1,tian+n+1,cmp);
sort(qi+1,qi+n+1,cmp);
memset(dp,-1,sizeof(dp));
int k=n+1-n;
cout<<f(1,n,k);
}