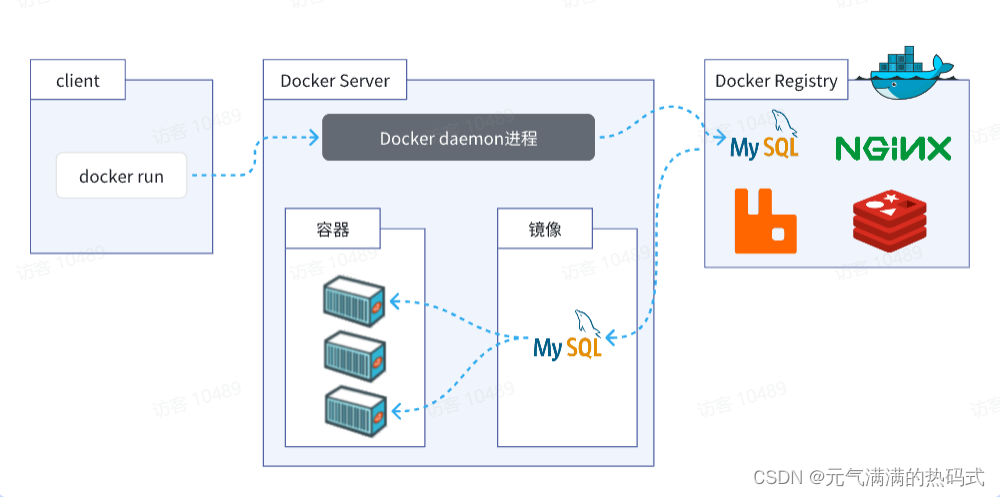
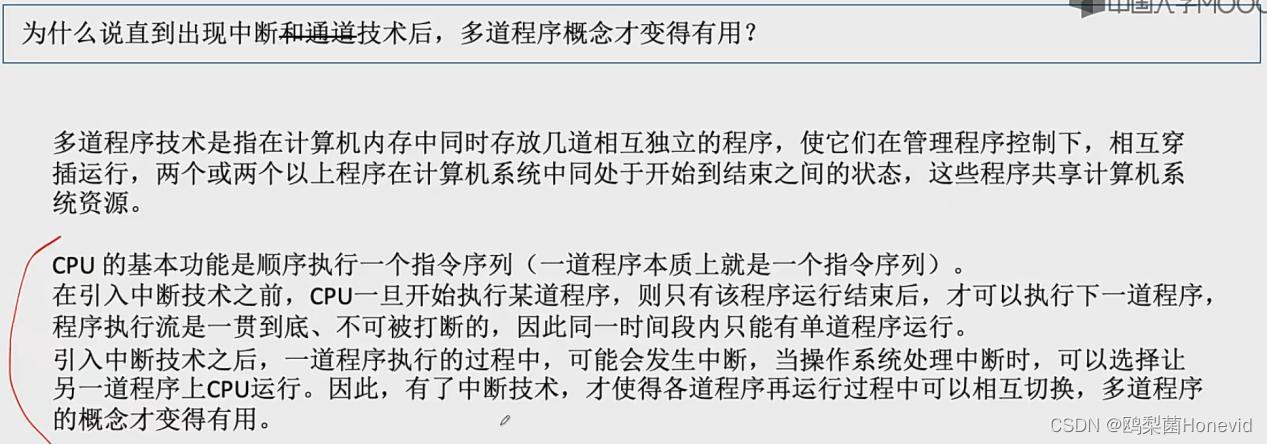
一、在线性代数中,符号 ( ||x|| ) 表示向量 ( x ) 的范数(Norm)。范数是一个将向量映射到非负值的函数,它衡量了向量的大小或长度。范数可以是多种类型,其中最常见的有:
-
欧几里得范数(L2范数): 对于一个实数或复数向量 (
),它的欧几里得范数定义为:
在二维空间中,欧几里得范数就是向量的长度,即从原点到向量所在点的距离。
-
L1范数: ( L1 ) 范数是向量元素绝对值之和,即:
它衡量了向量元素绝对值之和。
-
无穷范数(Infinity范数):
范数是向量元素绝对值中的最大值,即:
它衡量了向量中最大的绝对值元素。
除了这些常见的范数之外,还有其他类型的范数,如 ( L_p ) 范数(( p ) 范数),其中 。范数的选择取决于具体的问题和应用场景。
因此,当看到符号 ( ||x|| ) 时,需要根据上下文来确定是哪种范数。通常情况下,若无特别说明,默认是指欧几里得范数(L2范数)。
对L2范数的求导:
假设有一个实数向量 ,它的L2范数(欧几里得范数)定义为:
如果要对 ( ) 求导数,我们首先定义一个辅助函数:
然后,我们对 中的每个分量 (
) 分别求偏导数。注意到
是一个复合函数,因此我们需要使用链式法则。
对于第 ( i ) 个分量 (),链式法则给出:
用更紧凑的矩阵形式表示:
这是L2范数关于向量 () 的梯度。
对L2范数的的平方的求导:
现在,我们可以对每个分量 () 求导数。因为每个 (
) 项与其他项无关,所以对每个 (
) 求导相当于对 (
) 求导,即:
所以,整体的梯度向量是:
或者用更紧凑的矩阵形式表示:
这是L2范数的平方关于向量 ( ) 的梯度。
对应点已知时最优变换求解介绍以及SVD代码示例-CSDN博客