线性判别分析（LDA）

news2024/11/22 16:10:26

一、说明

        LDA 是一种监督降维和分类技术。其主要目的是查找最能分隔数据集中两个或多个类的特征的线性组合。LDA 的主要目标是找到一个较低维度的子空间，该子空间可以最大限度地区分不同类别，同时保留与歧视相关的信息。

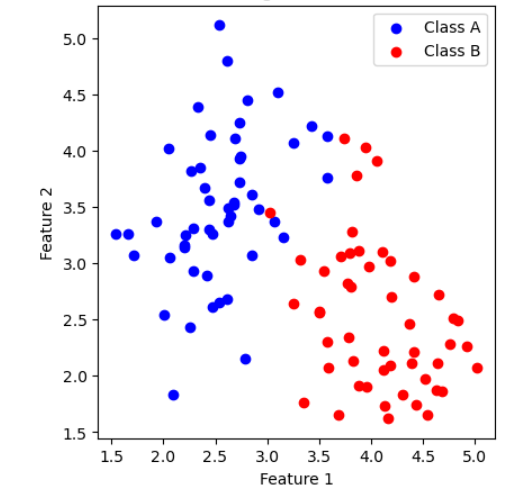
        LDA 是受监督的，这意味着它需要了解类标签或类别。它试图在数据空间中找到最能区分类的方向（特征的线性组合）。LDA 使类间方差与类内方差的比率最大化。它通过查找要素的线性组合来实现，这些要素可以最大限度地提高类之间的可分离性。

        然而，一个问题是，LDA与PCA有什么区别。LDA 面向分类和最大化类分离，而 PCA 则更通用，侧重于捕获数据方差

        让我们看看计算数据集的 LDA 所涉及的步骤

二、步骤1：数据收集

        让我们从一个数据集开始，其中包含来自两个类（A 类和 B 类）以及两个特征（特征 1 和特征 2）的样本。

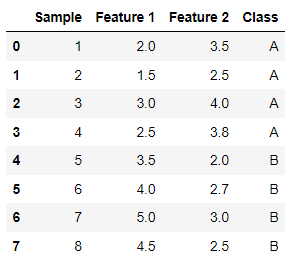
三、步骤 2：计算类均值

计算两个要素的每个类（A 类和 B 类）的平均向量。

A 类的平均向量：

Mean(Feature 1) = (2.0 + 1.5 + 3.0 + 2.5) / 4 = 2.5
Mean(Feature 2) = (3.5 + 2.5 + 4.0 + 3.8) / 4 = 3.45

B 类的平均向量：

Mean(Feature 1) = (3.5 + 4.0 + 5.0 + 4.5) / 4 = 4.25
Mean(Feature 2) = (2.0 + 2.7 + 3.0 + 2.5) / 4 = 2.55

四、步骤 3：计算类内散点矩阵 （SW）

SW 表示数据集的类内散点矩阵。它衡量每个类内数据的分布

要计算数据集的类内散点矩阵 （SW），您需要分别计算每个类的协方差矩阵，然后将它们相加。让我们一步一步地计算 A 类的 SW：

1.让我们将 A 类的平均向量表示为 ，我们已经计算过了：μ_A

μ_A = [Mean(Feature 1), Mean(Feature 2)] = [2.25, 3.45]

2.计算A类的协方差矩阵

A 类的协方差矩阵计算如下：

Covariance Matrix for Class A (S_A) = Σ [(x - Mean Vector for Class A) * (x - Mean Vector for Class A)^T]
Sample 1 (Class A):
Feature 1: 2.0
Feature 2: 3.5

Calculate differences:
Diff1 = 2.0 - 2.25 = -0.25
Diff2 = 3.5 - 3.45 = 0.05

Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (-0.25 * -0.25) / 3 = 0.0417 
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (-0.25 * 0.05) / 3 = -0.0042 
Sample 2 (Class A):
Feature 1: 1.5
Feature 2: 2.5

Calculate differences:
Diff1 = 1.5 - 2.25 = -0.75
Diff2 = 2.5 - 3.45 = -0.95

Covariance Matrix elements for Sample 2:
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (-0.75 * -0.75) / 3 = 0.1875
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (-0.75 * -0.95) / 3 = 0.2375
Sample 3 (Class A):

Feature 1: 3.0
Feature 2: 4.0
Calculate differences:

Diff1 = 3.0 - 2.25 = 0.75
Diff2 = 4.0 - 3.45 = 0.55
Covariance Matrix elements for Sample 3:

Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (0.75 * 0.75) / 3 = 0.1875
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (0.75 * 0.55) / 3 = 0.1375
Sample 4 (Class A):

Feature 1: 2.5
Feature 2: 3.8
Calculate differences:

Diff1 = 2.5 - 2.25 = 0.25
Diff2 = 3.8 - 3.45 = 0.35

Covariance Matrix elements for Sample 4:
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (0.25 * 0.25) / 3 = 0.04
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (0.25 * 0.35) / 3 = 0.029

A 类的协方差矩阵：

| Cov(Feature 1, Feature 1)    Cov(Feature 1, Feature 2) |
| Cov(Feature 2, Feature 1)    Cov(Feature 2, Feature 2) |
Covariance Matrix for Sample 1 (S1_A):
[[0.25, -0.025],
 [-0.025, 0.0025]]

Covariance Matrix for Sample 2 (S2_A):
[[1.0, 0.95],
 [0.95, 0.9025]]

Covariance Matrix for Sample 3 (S3_A):
[[0.25, 0.275],
 [0.275, 0.3025]]

Covariance Matrix for Sample 4 (S4_A):
[[0.0, 0.0],
 [0.0, 0.1225]]
S_A = S1_A + S2_A + S3_A + S4_A

代入计算值：

S_A =| 0.0417   -0.0042 |
     | 0.2375    0.0417  |

同样，我们可以计算 B 类的协方差矩阵

Sample 5 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (-0.625 * -0.625) = 0.390625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (-0.625 * -0.55) = 0.34375
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (-0.55 * -0.625) = 0.34375
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (-0.55 * -0.55) = 0.3025
Sample 6 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (-0.125 * -0.125) = 0.015625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (-0.125 * 0.15) = -0.01875
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (0.15 * -0.125) = -0.01875
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (0.15 * 0.15) = 0.0225
Sample 7 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (0.875 * 0.875) = 0.765625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (0.875 * 0.45) = 0.39375
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (0.45 * 0.875) = 0.39375
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (0.45 * 0.45) = 0.2025
Sample 8 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (0.375 * 0.375) = 0.140625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (0.375 * -0.05) = -0.01875
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (-0.05 * 0.375) = -0.01875
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (-0.05 * -0.05) = 0.0025
S_B = S5_B + S6_B + S7_B + S8_B
S_B = [[1.3125, 0.7],
       [0.7, 0.53]]

计算类内散点矩阵 （SW）。将两个类的协方差矩阵相加即可得到 SW：

Within-Class Scatter Matrix (SW)
=S_A+S_B=S_W 
= [0.0833 + 0.765625, -0.000833 + 0.39375]
  [-0.000833 + 0.39375, 0.0025 + 0.2025]


S_W = [0.848925, 0.393917]
      [0.392917, 0.205]

五、步骤 4：计算特征值和特征向量

在计算上，可以找到：

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(S_W)

从数学上讲，这可以找到：

  1. 计算S_W的倒数：

计算类内散点矩阵的逆数，表示为 S_W⁻¹。如果S_W不可逆，则可以使用伪逆。

S_W^(-1) = | 10.8103  -20.7762 |
          | -20.7762  44.7628  |

2.S_W^（-1）和S_B的乘积

S_W^(-1) * S_B = | 13.344  -6.953 |
                | -4.543  11.953 |

3.To 找到特征值 （λ），您需要求解特征方程，该方程由下式给出：

|S_W^(-1) * S_B - λ * I| = 0

I是单位矩阵

| 13.344 - λ  -6.953 |
| -4.543   11.953 - λ |

        可以通过将每个特征值代入方程并求解相应的特征向量来找到特征向量。S_W^(-1) * S_B * v = λ * vv

六、步骤 5：对特征值进行排序

        获得特征值后，按降序对它们进行排序以确定其重要性。您可以按如下方式在数学上表示这一点：

        设特征值表示为 λ_1、λ_2、...、λ_p （其中 p 是要素或维度的数量）。

        按降序对特征值进行排序：


λ_1 >= λ_2 >= ... >= λ_p

七、第 6 步：选择组件

        现在，您可以选择顶部特征值，其中是所需的降维水平。让我们将其表示为选择最大的特征值：kkk

λ_1, λ_2, ..., λ_k

        这些特征值表示数据中最重要的判别方向。k

八、第 7 步：项目数据

        选择特征值后，可以使用相应的特征向量将原始数据投影到新的低维空间上。此步骤降低了数据的维度，同时保留了最相关的信息。kk

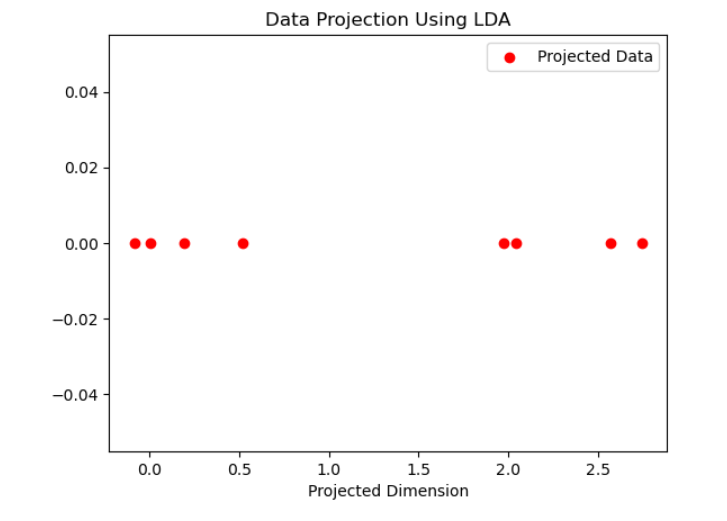
        使用线性判别分析 （LDA） 中选定的特征向量将数据投影到低维空间上

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1446003.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Mom系统初步认知

Mom系统初步认知

什么是MOM系统？ MOM指制造运营管理，是Manufacturing Operation Management的缩写；指通过协调管理企业的人员、设备、物料和能源等资源，把原材料或零件转化为产品的活动。MOM系统集成了生产计划、库存管理、生产调度、质量管理、设备维护、人员管理等功能，以实现生产效率和…
阅读更多...
web前端项目-进击的玉兔【附源码】

web前端项目-进击的玉兔【附源码】

进击的玉兔 【进击的玉兔】是一款基于Web前端技术的游戏&#xff0c;其主题和背景与中国的传统文化和神话有关。在游戏中&#xff0c;玩家需要通过解决各种难题和挑战来收集月饼&#xff0c;最终达成游戏目标。 运行效果&#xff1a; HTML源码&#xff1a; <!DOCTYPE h…
阅读更多...
Android13新特性之预测返回手势

Android13新特性之预测返回手势

Android14新特性之预测返回手势 简介 Android 14引入了对预测性返回手势的支持&#xff0c;这意味着开发者可以通过系统提供的额外动画和API来实现定制化的动画效果。这一更新使得应用程序可以在用户执行返回手势时展示一个动画预览&#xff0c;例如在应用程序前显示Home屏幕…
阅读更多...
Makefile编译原理 make 中的路径搜索_2

Makefile编译原理 make 中的路径搜索_2

一.make中的路径搜索 VPATH变量和vpath关键字同时指定搜索路径。 实验1 VPATH 和 vpath 同时指定搜索路径 mhrubuntu:~/work/makefile1/18$ tree . ├── inc │ └── func.h ├── main.c ├── makefile ├── src1 │ └── func.c └── src2 └── func.c mak…
阅读更多...
FRP内网穿透如何避免SSH暴力破解（二）——指定地区允许访问

FRP内网穿透如何避免SSH暴力破解（二）——指定地区允许访问

背景 上篇文章说到&#xff0c;出现了试图反复通过FRP的隧道&#xff0c;建立外网端口到内网服务器TCP链路的机器人&#xff0c;同时试图暴力破解ssh。这些连接造成了流量的浪费和不必要的通信开销。考虑到服务器使用者主要分布在A、B、C地区和国家&#xff0c;我打算对上一篇…
阅读更多...
万维网的文档

万维网的文档

目录 1 万维网的文档 动态万维网文档 CGI CGI 网关程序 活动万维网文档 用 Java 语言创建活动文档 1 万维网的文档 分为&#xff1a; 静态万维网文档。内容不会改变。简单。(html、xml、css) 动态万维网文档。文档的内容由应用程序动态创建。 活动万维网文档。由浏览器端…
阅读更多...
npm config set registry https://registry.npm.taobao.org 这个设置了默认的镜像源之后如何恢复默认的镜像源

npm config set registry https://registry.npm.taobao.org 这个设置了默认的镜像源之后如何恢复默认的镜像源

要恢复npm默认的镜像源&#xff0c;你可以使用以下命令将registry设置回npm的官方源&#xff1a; npm config set registry https://registry.npmjs.org/这个命令会修改你的全局npm配置&#xff0c;将包的下载源改回npm官方的源。这样做之后&#xff0c;任何后续的npm install…
阅读更多...
【二叉树】层序遍历

【二叉树】层序遍历

目录 层序遍历概念&结构 层序遍历的实现 整体思路 代码实现 图示理解 BT升级 整体思路 代码实现 图示理解​ 应用 题目 前序&中序&后序遍历&#xff1a;深度优先遍历dfs 层序遍历&#xff1a;广度优先遍历bfs 层序遍历概念&结构 层序遍历&#xf…
阅读更多...
【java语言基础⑥】面向对象——面向对象的思想、类与对象

【java语言基础⑥】面向对象——面向对象的思想、类与对象

1.学习目标 了解面向对象的思想&#xff0c;能够说出面向对象的三个特性掌握类的定义&#xff0c;能够独立完成类的定义掌握对象的创建和使用&#xff0c;能够完成对象创建&#xff0c;用对象访问对象属性和方法掌握对象的引用传递&#xff0c;能够独立实现对象的引用传递熟悉…
阅读更多...
力扣_字符串6—最小覆盖字串

力扣_字符串6—最小覆盖字串

题目 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串&#xff0c;则返回空字符串 “” 。 示例 &#xff1a; 输入&#xff1a;s “ADOBECODEBANC”, t “ABC” 输出&#xff1a;“BANC” 解释&#xff1a;…
阅读更多...
Java安全 URLDNS链分析

Java安全 URLDNS链分析

Java安全 URLDNS链分析 什么是URLDNS链URLDNS链分析调用链路HashMap类分析URL类分析 exp编写思路整理初步expexp改进最终exp 什么是URLDNS链 URLDNS链是Java安全中比较简单的一条利用链&#xff0c;无需使用任何第三方库&#xff0c;全依靠Java内置的一些类实现&#xff0c;但…
阅读更多...
mxxWechatBot主动发送消息至微信

mxxWechatBot主动发送消息至微信

大家好&#xff0c;我是雄雄&#xff0c;欢迎关注微信公众号&#xff1a;雄雄的小课堂。 免责声明&#xff1a;该工具仅供学习使用&#xff0c;禁止使用该工具从事违法活动&#xff0c;否则永久拉黑封禁账号&#xff01;&#xff01;&#xff01;本人不对任何工具的使用负责&am…
阅读更多...
【Git版本控制 05】多人协作

【Git版本控制 05】多人协作

目录 一、邀请开发用户 二、新建远程分支 三、拉取远程分支 四、推送远程分支 五、合并远程分支 六、多分支协作 一、邀请开发用户 在windows环境下&#xff0c;再clone同⼀个项⽬仓库&#xff0c;来模拟⼀起协作开发的另⼀名⼩伙伴。 际开发中&#xff0c;每个⽤⼾都有…
阅读更多...
【Web】超级详细的Linux权限提升一站式笔记

【Web】超级详细的Linux权限提升一站式笔记

目录 一、Linux内核提权 提权原理 提权环境 提权复现 二、SUID提权 SUID介绍 设置SUID SUID提权原理 查找SUID文件 提权介绍 find提权 bash提权 vim提权 python提权 三、计划任务提权 提权原理 提权环境 提权步骤 四、环境变量劫持提权 提权原理 提权环境…
阅读更多...
【机器学习】卷积和反向传播

【机器学习】卷积和反向传播

一、说明 自从 AlexNet 在 2012 年赢得 ImageNet 竞赛以来&#xff0c;卷积神经网络 (CNN) 就变得无处不在。从不起眼的 LeNet 到 ResNets 再到 DenseNets&#xff0c;CNN 无处不在。 您是否想知道 CNN 的反向传播中会发生什么&#xff0c;特别是反向传播在 CNN 中的工作原理。…
阅读更多...
【知识整理】技术新人的培养计划

【知识整理】技术新人的培养计划

一、培养计划落地实操 1. 概要 新人入职&#xff0c;要给予适当的指导&#xff0c;目标&#xff1a; 1、熟悉当前环境&#xff1a; 生活环境&#xff1a;吃饭、交通、住宿、娱乐 工作环境&#xff1a;使用的工具&#xff0c;Mac、maven、git、idea 等 2、熟悉并掌握工作技…
阅读更多...
Android---Jetpack Compose学习003

Android---Jetpack Compose学习003

Compose 状态。本文将探索如何在使用 Jetpack Compose 时使用和考虑状态&#xff0c;为此&#xff0c;我们需要构建一个 TODO 应用&#xff0c;我们将构建一个有状态界面&#xff0c;其中会显示可修改的互动式 TODO 列表。 状态的定义。在科学技术中&#xff0c;指物质系统所处…
阅读更多...
【C深度解剖】前置++与后置++

【C深度解剖】前置++与后置++

简介&#xff1a;本系列博客为C深度解剖系列内容&#xff0c;以某个点为中心进行相关详细拓展 适宜人群&#xff1a;已大体了解C语法同学 作者留言&#xff1a;本博客相关内容如需转载请注明出处&#xff0c;本人学疏才浅&#xff0c;难免存在些许错误&#xff0c;望留言指正 作…
阅读更多...
相机图像质量研究(12)常见问题总结：光学结构对成像的影响--炫光

相机图像质量研究(12)常见问题总结：光学结构对成像的影响--炫光

系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结&#xff1a;光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结&#xff1a;光学结构对成…
阅读更多...
关于Navicat导入sql文件后er图乱序问题

关于Navicat导入sql文件后er图乱序问题

关于Navicat导入sql文件后er图乱序问题 具体操作如下&#xff1a; 点击左下角刷新旁边的小三角
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023