目录
单粒子模拟
显式欧拉方法
改进
中点法/修正的欧拉方法
自适应步长
隐式欧拉方法
非物理改变位置(Position-Based / Verlet Integration)
刚体模拟
流体模拟
单粒子模拟
先来研究粒子的运动,假设有一个速度矢量场,对于确定的位置和时间可以确定粒子的速度
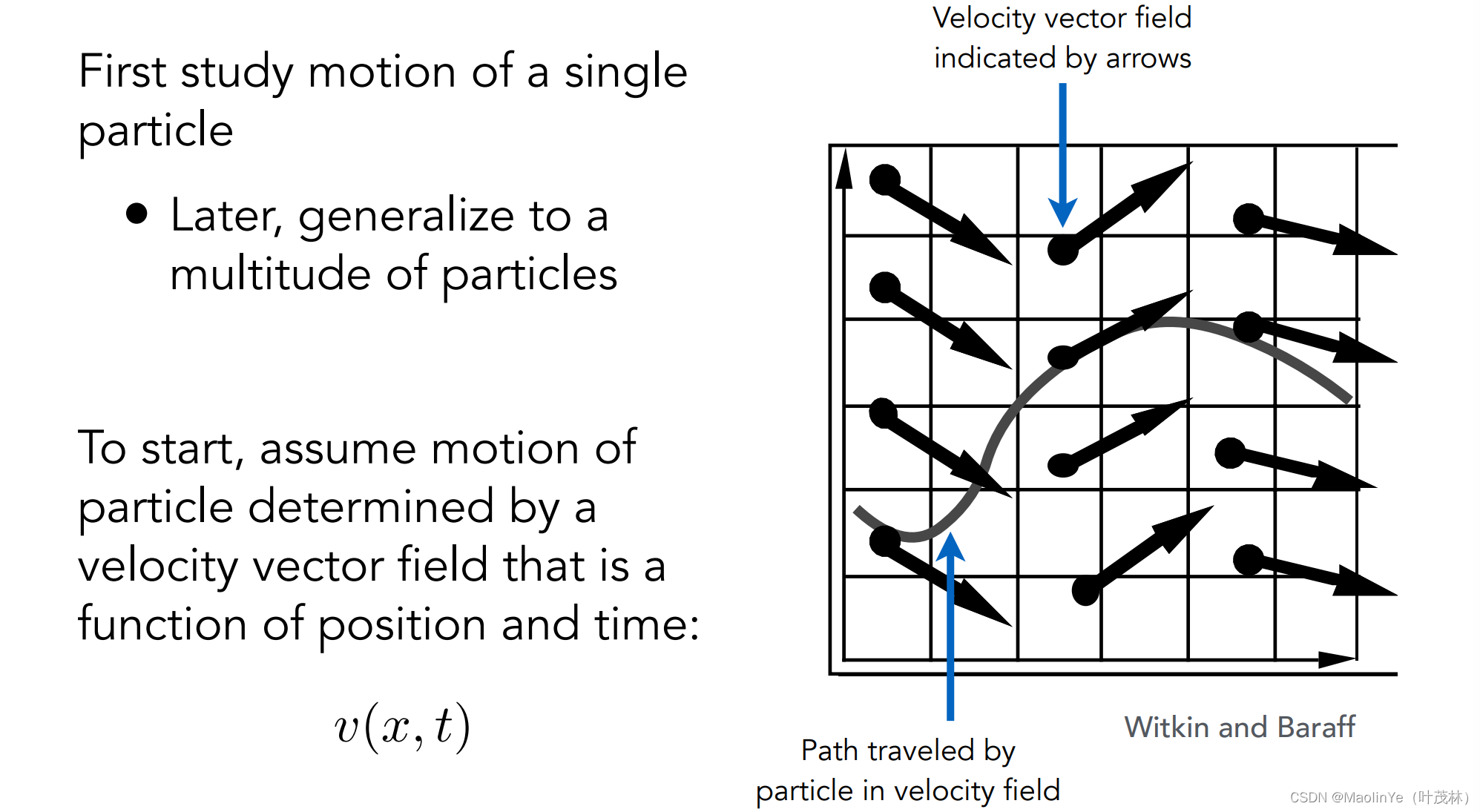
就会有一个计算粒子随时间的位置的一阶常微分方程Ordinary Differential Equation (ODE),一阶表示只有一阶的导数,常表示没有偏导

显式欧拉方法
显式的欧拉方法或者说是前向的欧拉方法就是用上一时刻t的位置加上上一时刻的速度乘以其间的时间间隔Δt来计算当前的位置,同样的方法计算出当前的速度
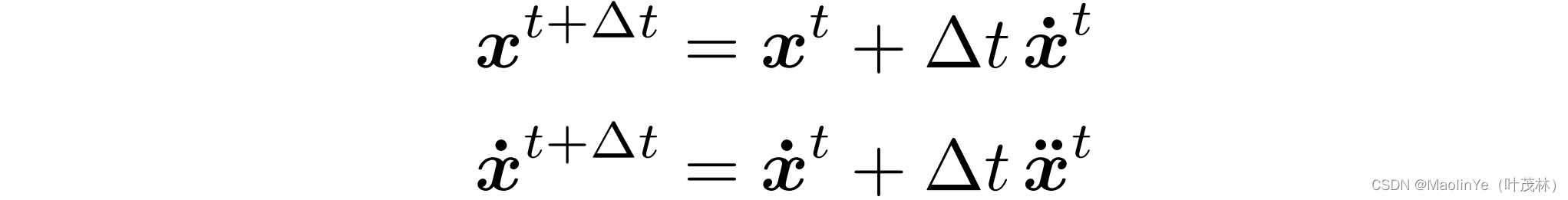
这个欧拉方法的误差和时间间隔Δt有关,这个间隔越小误差越小,间隔越大误差就越大,并且这个误差会因为积累而变得越来越大
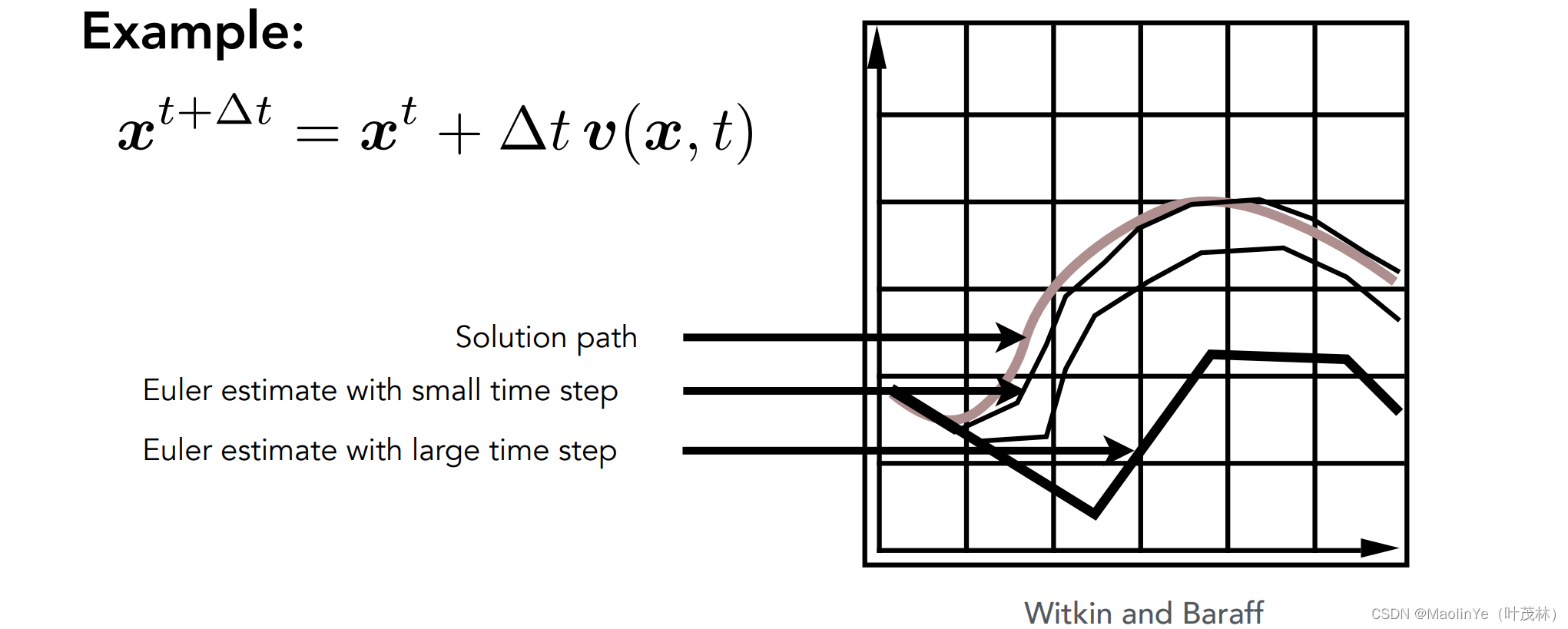
减小Δt可以减小显式欧拉方法的误差,但是不能改变它的不稳定性,归根结底是因为这个步长无论取的多小始终是无法赶上速度场的变化,并且一旦出现了偏差就会继续累计

改进
中点法/修正的欧拉方法
我先算Δt/2时刻的位置,然后取这个中点位置的速度来计算下一时刻的位置

也就是取这个步长时间内的平均速度来计算下一时刻的位置
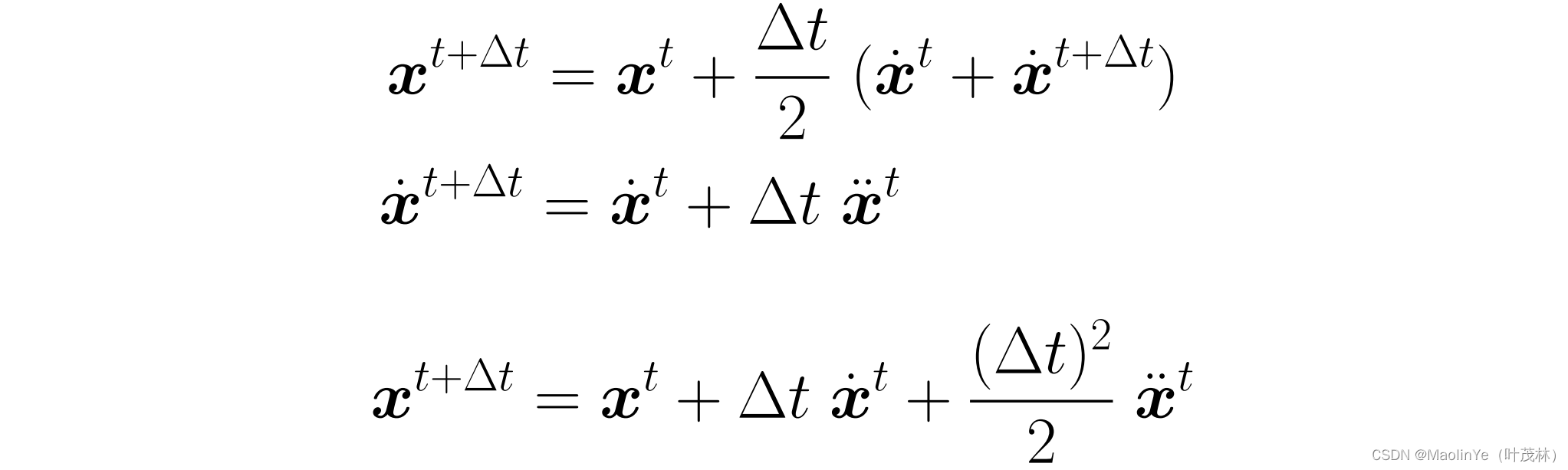
自适应步长
哎这个就很简单了,就是我先用Δt算一次结果,再用Δt/2算一次结果,如果两次结果差别不大,那我就停下来,这个结果就算出来了,否则的话我就以这个Δt/2的结果继续比较计算Δt/4的结果,这样继续算下去
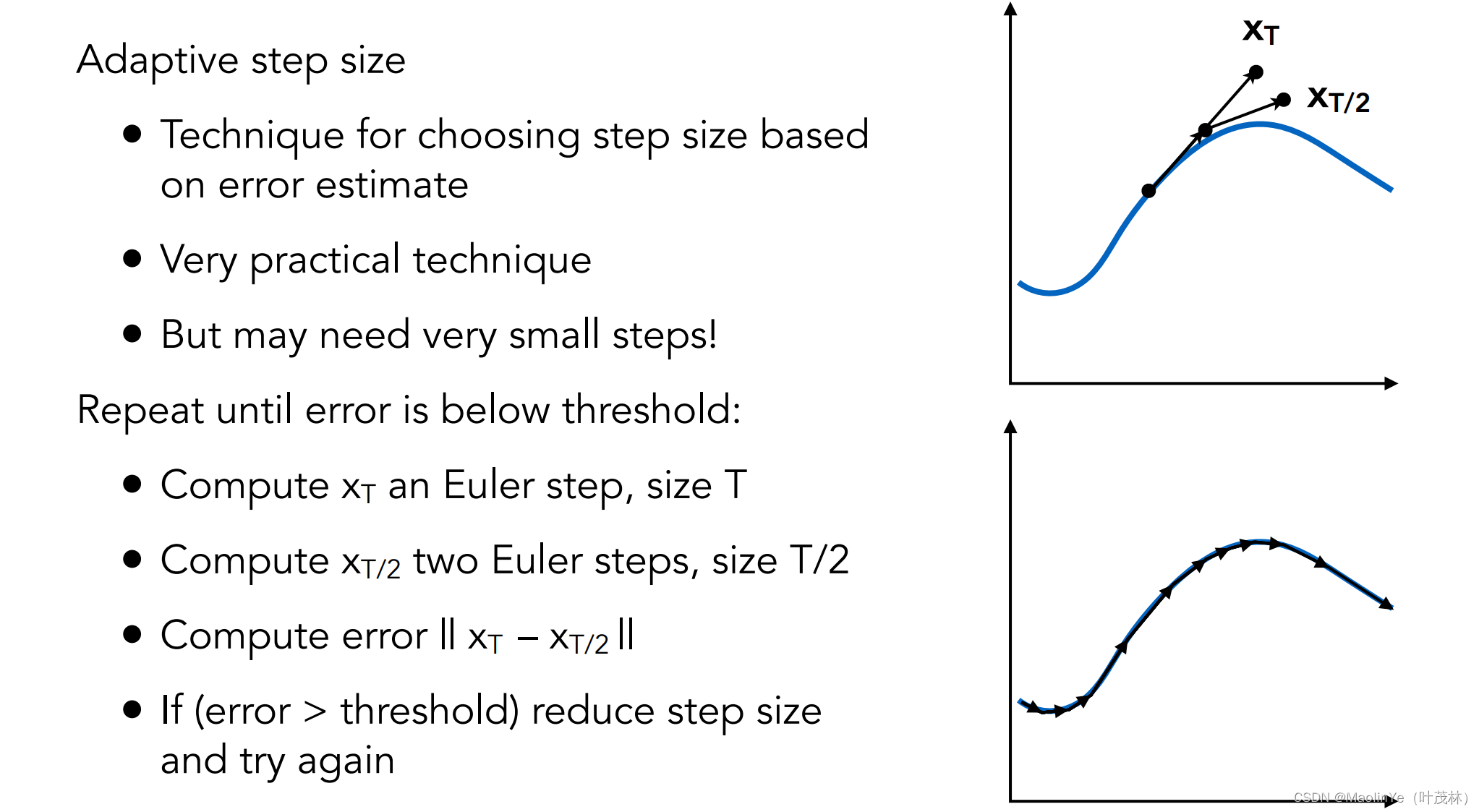
隐式欧拉方法
我们之前显式的欧拉方法是用上一时刻的速度和加速度来计算当前时刻,那么用下一时刻的速度和加速度来计算当前时刻的就叫作隐式的欧拉方法或者说是后向的欧拉方法
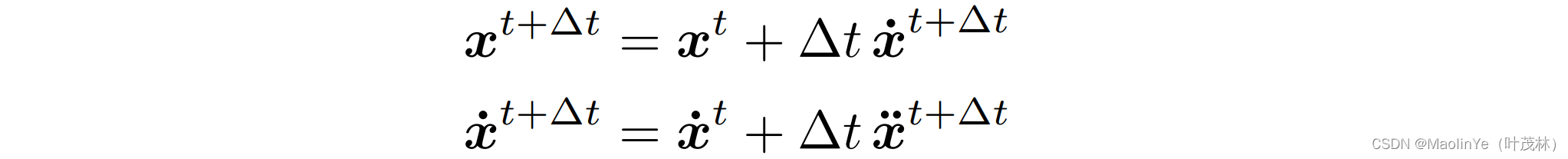
我们把这个每个步长产生的误差叫做局部误差,总体累积的误差叫做全局误差,我们不关心数据的大小,关心这个误差的阶数,像这个隐式的欧拉方法它的局部误差的阶就是二次的,全局误差的阶是一次的,也就是说,当步长减少一半的时候,全局误差也会减少一半,也就是阶数越高误差下降的越快

有一类方法,叫做龙格库塔(Runge-Kutta Families),非常适合用来解这个常微分方程,并且它有一个误差的控制是四阶的方法

非物理改变位置(Position-Based / Verlet Integration)
这个实现很简单,什么呢?就是我直接去改变这个位置来满足某种约束,比如弹簧,当弹簧拉伸到某种程度立刻调整弹簧两个端点回到初始位置

刚体模拟
所谓刚体就是说它不会发生形变,也就是这个刚体内部的所有粒子的运动都是一样,那么就可以把它当成一颗粒子对待,但是会考虑更多的属性,像位置、旋转的角度、速度和角速度,以及它们对时间的导数

流体模拟
这里是Position-Based的一个简单应用,比如模拟水,我假设水是由很多刚体小球组成的并且这个水不可压缩,那也就是说水的密度应该是到处一样的,也就是水的某个地方里的刚体小球是一样的,一旦密度发生变化,就通过改变小球的位置使某处的小球数量恢复,也就是需要知道某处密度相对于小球位置的梯度通过梯度下降法来实现

这里有两种方法或者说是两种视角来模拟这种大量的物质
一个是质点法,也叫拉格朗日方法或者拉格朗日视角,就是对于每个个体进行模拟

还有一个是网格法,也叫欧拉方法或者是欧拉视角,也就是把空间分成很多网格,对于每个网格去研究它里面的东西随时间会发生什么变化

这两个方法也可以结合使用,叫做物质点方法或者材质点方法,Material Point Method (MPM),怎么做呢?我先考虑每个粒子的属性,然后在网格里面考虑粒子之间的整体作用并记录在网格里面,再对于网格里面的粒子去更新它们的状态

完结撒花,用了这个寒假学了games101课程并一直坚持把这个笔记做完,我一开始是先学这个OpenGL,发现确实很多概念不是很懂,然后来学games101,然后就非常的通透,目前games101作业还在做,估计这个寒假可以完成,再做几个小项目,希望能冲上游戏开发的岗位,唉大三了,希望能够顺利找到理想的暑期实习