Pytorch卷积层原理和示例 nn.Conv1d卷积 nn.Conv2d卷积

news2024/11/26 4:31:49

内容列表

一，前提
二，卷积层原理
1.概念
2.作用
3. 卷积过程
三，nn.conv1d
1，函数定义：
2, 参数说明:
3,代码:
4, 分析计算过程
四，nn.conv2d
1, 函数定义
2, 参数：
3, 代码
4, 分析计算过程

一，前提

在开始前，要使用pytorch实现以下内容，需要掌握tensor和的用法

二，卷积层原理

1.概念

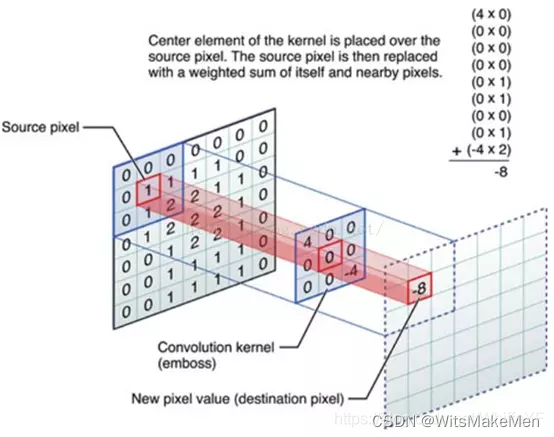
卷积层是用一个固定大小的矩形区去席卷原始数据，将原始数据分成一个个和卷积核大小相同的小块，然后将这些小块和卷积核相乘输出一个卷积值（注意这里是一个单独的值，不再是矩阵了）。

2.作用

特征提取

卷积的本质就是用卷积核的参数来提取原始数据的特征，通过矩阵点乘的运算，提取出和卷积核特征一致的值，如果卷积层有多个卷积核，则神经网络会自动学习卷积核的参数值，使得每个卷积核代表一个特征。

3. 卷积过程

在这里插入图片描述

三，nn.conv1d

这里我们拿最常用的conv1d举例说明卷积过程的计算。

conv1d是一维卷积，它和conv2d的区别在于只对宽度进行卷积，对高度不卷积。

1，函数定义：

torch.nn.functional.conv1d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)

2, 参数说明:

**input：**输入的Tensor数据，格式为(batch,channels,W)，三维数组，第一维度是样本数量，第二维度是通道数或者记录数。三维度是宽度。

**weight：**卷积核权重，也就是卷积核本身。是一个三维数组，(out_channels, in_channels/groups, kW)。out_channels是卷积核输出层的神经元个数，也就是这层有多少个卷积核；in_channels是输入通道数；kW是卷积核的宽度。

**bias：**位移参数，可选项，一般也不用管。

**stride：**滑动窗口，默认为1，指每次卷积对原数据滑动1个单元格。

**padding：**是否对输入数据填充0。Padding可以将输入数据的区域改造成是卷积核大小的整数倍，这样对不满足卷积核大小的部分数据就不会忽略了。通过padding参数指定填充区域的高度和宽度，默认0（就是填充区域为0，不填充的意思）

**dilation：**卷积核之间的空格，默认1。

**groups：**将输入数据分组，通常不用管这个参数，没有太大意义。

3,代码:

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

a=range(16)
x = Variable(torch.Tensor(a))
'''
a: range(0, 16)
x: tensor([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12., 13.,
        14., 15.])
'''

x=x.view(1,1,16)
'''
x variable: tensor([[[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12., 13., 14., 15.]]])
'''

b=torch.ones(3)
b[0]=0.1
b[1]=0.2
b[2]=0.3
weights = Variable(b)
weights=weights.view(1,1,3)
'''
weights: tensor([[[0.1000, 0.2000, 0.3000]]])
'''

y=F.conv1d(x, weights, padding=0)
'''
y: tensor([[[0.8000, 1.4000, 2.0000, 2.6000, 3.2000, 3.8000, 4.4000, 5.0000, 5.6000, 6.2000, 6.8000, 7.4000, 8.0000, 8.6000]]])
'''

上面出现了 x.view(1,1,16) view的用法参考我之前的博客
Pytorch-view的用法
上面出现了 Variable(torch.Tensor(a)) Tensor和Variable的用法参考我之前的博客
pytorch入门 Variable 用法
PyTorch Tensor的初始化和基本操作

4, 分析计算过程

（1）原始数据大小是0-15的一共16个数字，卷积核宽度是3，向量是[0.1,0.2,0.3]。我们看第一个卷积是对x[0:3]共3个值[0,1,2]进行卷积，公式如下：

00.1+10.2+2*0.3=0.8
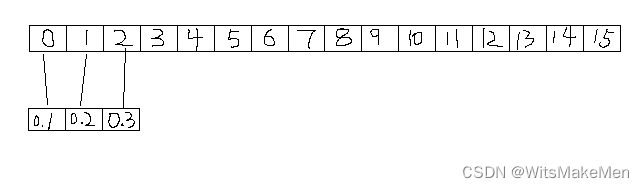
在这里插入图片描述

（2）对第二个目标卷积，是x[1:4]共3个值[1,2,3]进行卷积，公式如下：

10.1+20.2+3*0.3=1.4
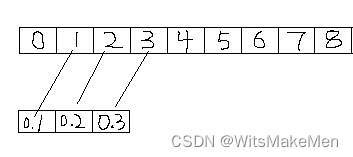
在这里插入图片描述

剩下的就以此类推

四，nn.conv2d

1, 函数定义

nn.Conv2d(self, in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True))

2, 参数：

in_channel:　输入数据的通道数，例RGB图片通道数为3；

out_channel: 输出数据的通道数，这个根据模型调整；
kennel_size: 卷积核大小，可以是int，或tuple；kennel_size=2,意味着卷积大小(2,2)， kennel_size=（2,3），意味着卷积大小（2，3）即非正方形卷积
stride：步长，默认为1，与kennel_size类似，stride=2,意味着步长上下左右扫描皆为2， stride=（2,3），左右扫描步长为2，上下为3；
padding：　零填充

3, 代码

import torch
import torch.nn as nn
from torch.autograd import Variable

r = torch.randn(5, 8, 10, 5) # batch, channel , height , width
print(r.shape)

r2 = nn.Conv2d(8, 14, (3, 2), (2,1))  # in_channel, out_channel ,kennel_size,stride
print(r2)

r3 = r2(r)
print(r3.shape)
torch.Size([5, 8, 10, 5])
Conv2d(8, 14, kernel_size=(3, 2), stride=(2, 1))
torch.Size([5, 14, 4, 4])