文章目录
- 前言
- 初级问题
- 后续问题
前言
首先说一点,将paper的pdf文件直接上传arxiv是不行的,arxiv要求我们要上传源文件,所以才这么麻烦。
初级问题
首先上传文件之后有可能会在下面这个界面出现问题,这里一般都比较常见的问题,需要按照红色提示修改。

这两个文件是必须的,a.tex,a.bbl,这里的a可以是你自己取的名字,但是这两个文件必须同名。然后那个a.bib文件好像不是必须的,这里就有一个疑问了,因为我们用overleaf的时候根本没有这个a.bbl文件呀,如下:
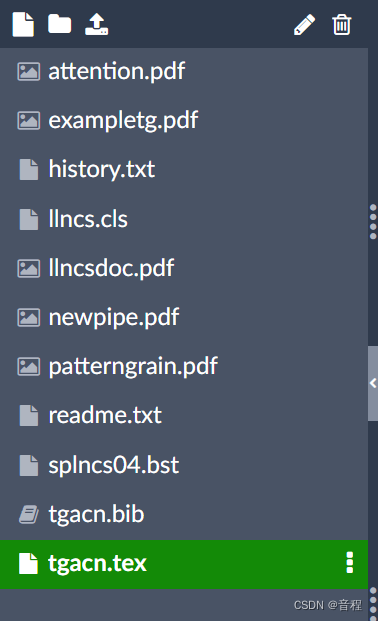
其实是有的,需要自己下载,在哪呢?如下,点击那个1的那个图标:
在这里,我们会看到一些红色错误以及蓝色警告,我们这里不管它,继续往下拉,
可以看到其他文件,我们点击那个。
我们发现有我们要的.bbl文件,
将这个下载下来,然后放到我们的目录里面,并且改一改名字,然后就可以了。
然后把这个目录压缩为.zip文件,上传到arxiv上就可以了。对了,这里提醒一下,你之前上传了格式不对的文件,arxiv系统不会帮你删,而会将文件叠加,所以最好你自己主动删除一下,那里有一个delete all,删除了之后再把上面这个正确的上传即可。
后续问题
如果上传之后没有什么提示,就可以点击下面这个。
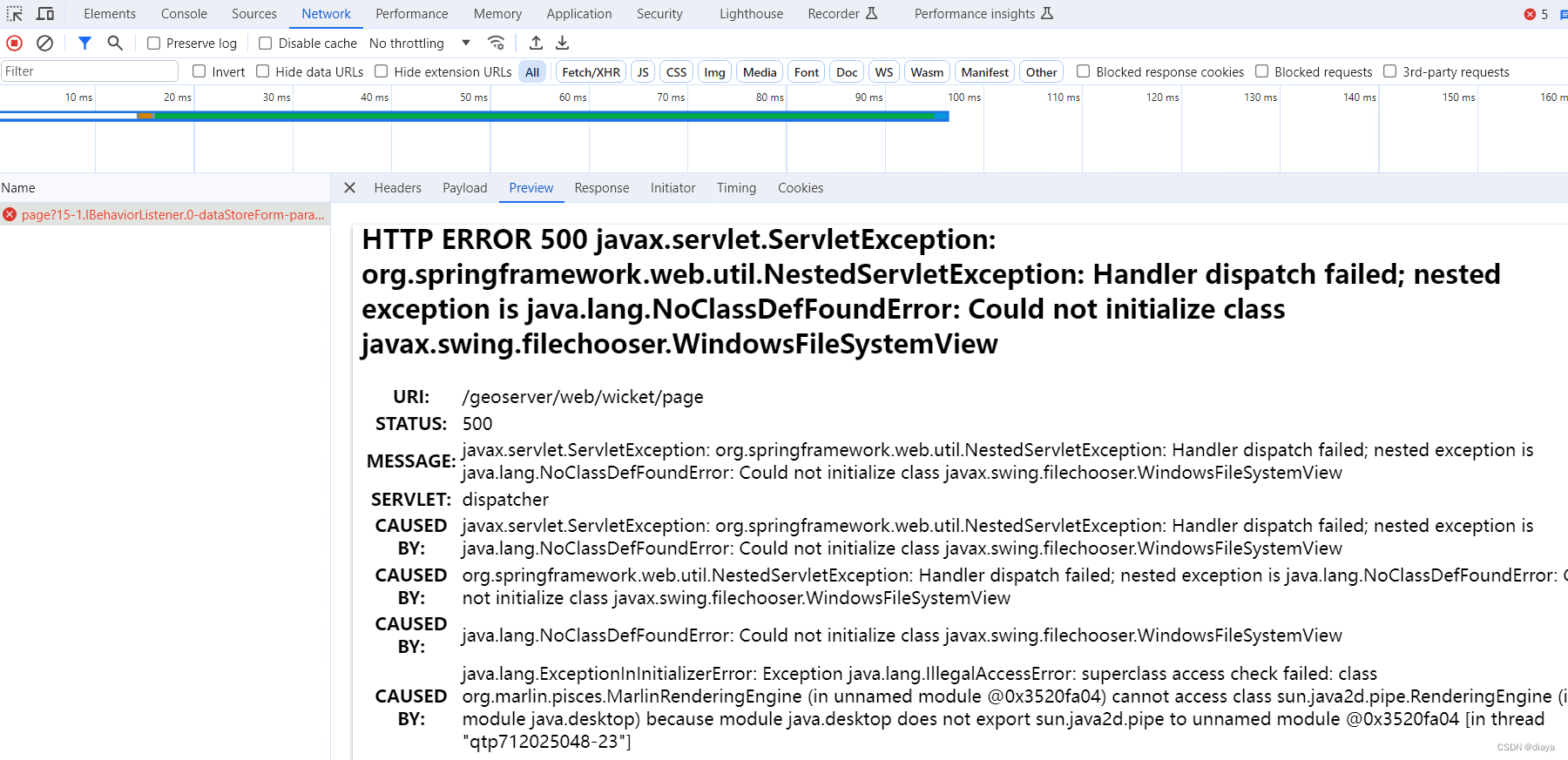
然而,点击这个之后仍然有可能会有后续的报错。例如下面这个。
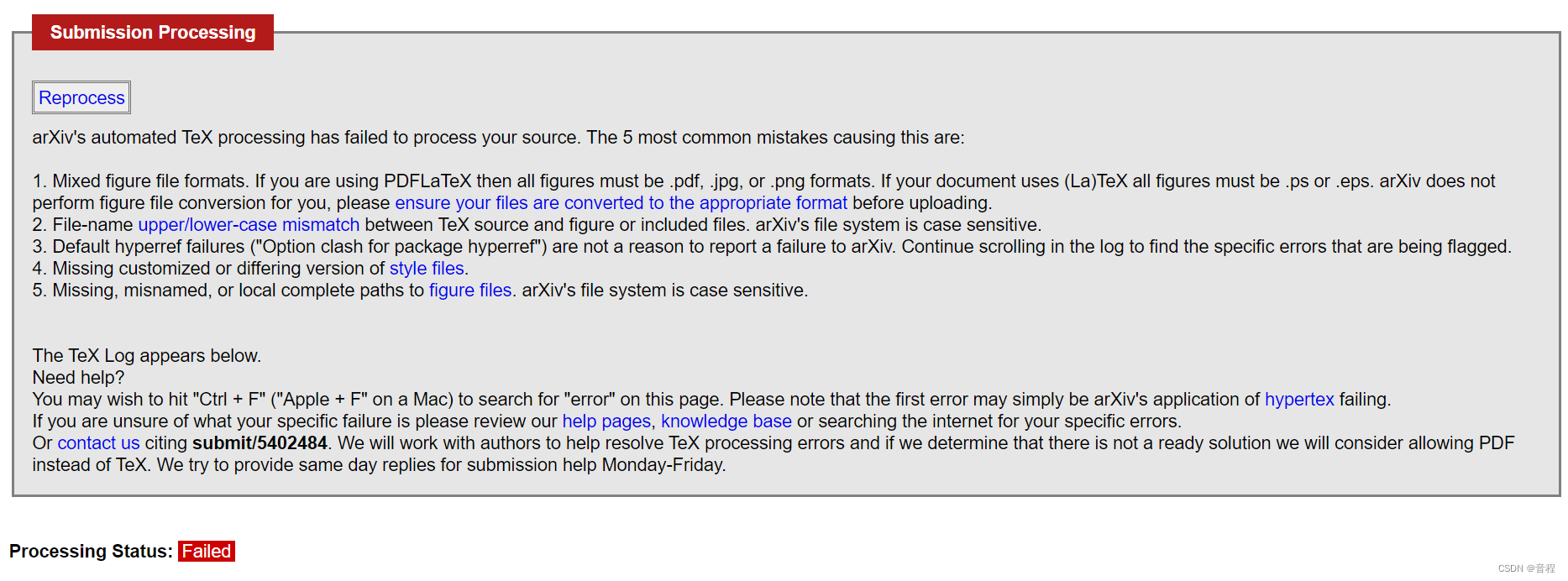
它上面给了我5个错误,但是这并不是说我这5个错误都有,也不是说我至少有其中之一的错误,这只是arxiv系统给出的常见错误。事实上,我的错误不是上面的错误。
我的错误如下:
We denote the above attention result as $channel(t)\in \mathbb{R}^{l\times l}$.
上面那个\mathbb需要宏包\usepackage{amssymb},但是我没有导入。这个错误其实overleaf已经提示我了,但是由于这个错误不足以产生不了pdf,只是字体样式不对而已,所以我没有太在意这个错误。但是,arxiv系统会在意!!!直接不给你产生pdf。。。
所以你赶紧去检查一下你在overleaf编译的时候有没有什么错误,不能只看能不能产生pdf!就算可以产生pdf,也有可能有错误!检查错误的方法是:1.看编辑界面有没有那种红色错误提示;
2.看编译界面有没有红色错误提示,还记得【本文初级问题】中的这张图吗?红色就表示还有错误。

总之,你把红色错误给解决,一般arxiv就可以编译成功了。
这里插一句嘴,其实arxiv系统也有编译的日志,输出在了你提交文件的那个界面,你可以看看日志,日志上面也会说你有什么错误(在红色提示前面那个就是你的错误),按照错误提示解决就可以了。

![[C#] 如何使用ScottPlot.WPF在WPF桌面程序中绘制图表](https://img-blog.csdnimg.cn/direct/8378963d0c9d4592925d7858d0944b02.png)