1049. 最后一块石头的重量Ⅱ

题目链接：1049. 最后一块石头的重量 II - 力扣（LeetCode）

思路

尽量将石头分为重量相同的两堆，这样两堆中的石头相撞之后剩下的石头就会最小。根据之前的01背包理论：

代码随想录算法训练营第四十五天（动态规划篇）|01背包-CSDN博客

代码随想录算法训练营第四十六天（动态规划篇）|01背包（滚动数组方法）-CSDN博客

可以设背包容量为石头重量总和的一半，求它所能装的最大价值，之后就能得到最后所剩的石头。

代码实现

class Solution(object):
    def lastStoneWeightII(self, stones):
        G1 = sum(stones)//2   
        G2 = sum(stones) - G1 
        dp = [0] * (G1 + 1)
        for num in stones:
            for j in range(G1, num - 1, -1):
                dp[j] = max(dp[j], dp[j - num] + num)
        return (G1 - dp[G1] + G2) - dp[G1]
        
       # e.g.  分为33，34两堆，如果容量为33的背包所装的最大价值为31，那相撞后的那块石头质量为（33 - 31 + 34) - 31
        

494. 目标和

题目链接：494. 目标和 - 力扣（LeetCode）

思路

把数组里的数分为两部分：前面符号为“+”，即要被加的数，和前面符号为“-”，即要被减的数。设所有参与加法的数和为x，参与减法的数和为y，则x-y = target，x+y=sum，联立得x = (target+sum)/2。因此题目就变成了寻找数组中和为(target+sum)/2的子集总和，转变为01背包问题，即能将容量为(target+sum)/2背包装满的方法。

1. dp数组定义

dp[j]: 将容量为j的背包装满的方法。

2. 递推公式

遍历数组中的数，每遍历到新的数nums[i]，相当于新加了一个物体，那么dp[j]（能装满容量为j的包的方法）就会发生变化，之前的方法加上当前物体所能贡献的那部分，当前物体可以帮着填充容量为j-nums[i]的包。因此，dp[j]因为nums[i]的到来，多了dp[j-nums[i]]种新方法。

所以递推公式为dp[j] += dp[j-nums[i]]

3. 初始条件

当背包容量为0，有1种方法，即什么都不选，dp[0] = 1

4. 递推顺序

使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历。

5. 举例推导dp数组

输入：nums：[1, 1, 1, 1, 1], S:3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

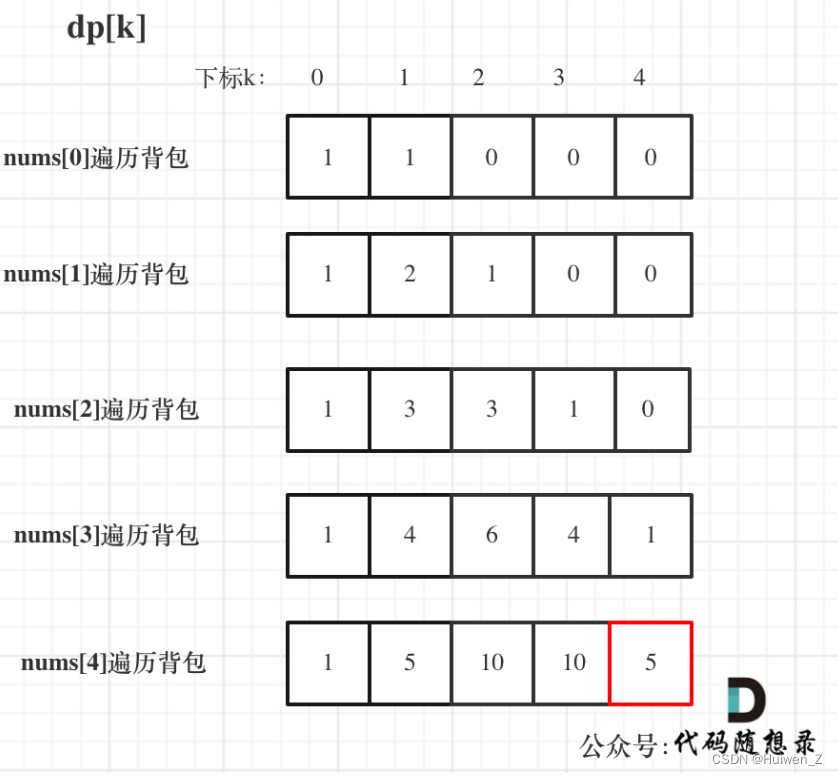
对于第一个数字1，只能填满容量为0和容量为1的背包，当考虑到第二个1时，可能填满的背包容量为1到S = 3。如果要填满容量为3的背包，就要看看已有的物体有多少种填满容量为2的包的方法，但没有（dp[2] = 0)，所以dp[3]只能保持为0。但新加入的物体1可以帮着填满容量为2的包，因为之前已经有一种方法可以装满容量为1的包了，因此dp[2] = 1。

代码实现

class Solution(object):
    def findTargetSumWays(self, nums, target):
        if abs(target) > sum(nums):   # 对于nums,最大能得到的数是全体非负整数相加，最小是最大值的负数，如果target超过次范围，则没有方法。
            return 0
        if (target + sum(nums))%2 == 1:
            return 0
        x = (sum(nums) + target)/2
        dp = [0] * (x + 1)
        dp[0] = 1
        for num in nums:
            for j in range(x, num - 1, -1):
                dp[j] += dp[j - num]
        return dp[x]