今天我们接着学习dfs（状态表示）。

1.抽象形式的dfs

前面用到的 DFS 算法都是比较容易想象出搜索过程的，接下来我们看一些不那么容易想象搜索过程的 DFS 过程，这些问题我们称为抽象形式的 DFS。

来回顾一下上节课遇到的一个问题：

给定 
n 个整数，要求选出 K 个数，使得选出来的 K 个数的和为 sum。

我们依然借助 DFS 来解决这个问题。对于每一个数，枚举选或者不选两种情况，我们可以用 DFS 思想来完成这样的枚举过程。

我们在搜索的过程中，用 
S 来记录当前选择的数值总和，
k 来记录选择的数的个数，deep 表示当前正在枚举第几个数是否选择。

在第一层 DFS 的时候，我们可以枚举是否选第一个数，如果选第一个数则让 
S 加上第一个数且 
k 加一，DFS 进入到下一层；否则 DFS 直接进入到下一层。当然，这里我们还需要借助全局变量、参数或修改数组中元素的值等方式来标识出当前的层数，为了减少篇幅，在下文中就直接忽略掉了。

在第二层，对第二个数做同样的处理，DFS 的过程中记录已经选取的数的个数，如果已经选取了 k 个数，判断 
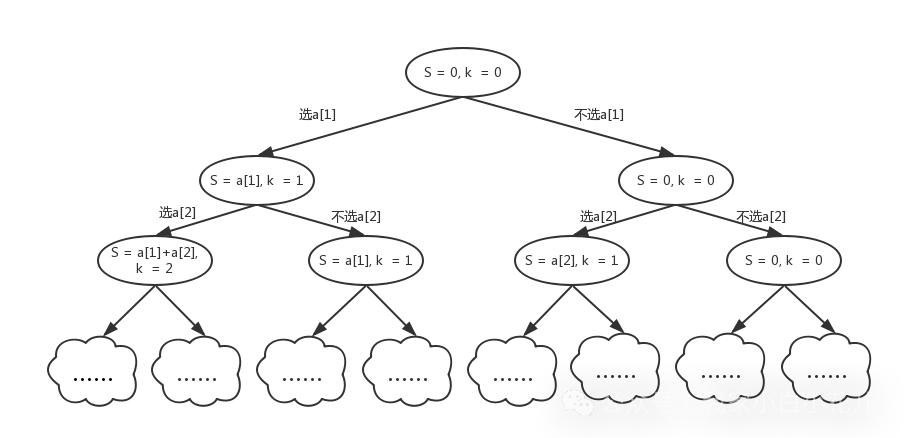
S 值是否等于sum。对于每一层，我们都有两个选择——选和不选。不同的选择，都会使得搜索进入完全不同的分支继续搜索。

下图是这个搜索过程对应的 搜索树，搜索树上的每一个结点都是一个 状态，一个状态包含两个值 S 和 k也就是一个状态对应当前的数值总和，以及选的数的个数。