机器学习系列——（十三）多项式回归

news2024/10/7 8:22:01

引言

在机器学习领域，线性回归是一种常见且简单的模型。然而，在某些情况下，变量之间的关系并不是线性的，这时候我们就需要使用多项式回归来建模非线性关系。多项式回归通过引入高次项来扩展线性回归模型，从而更好地拟合数据。本文将详细介绍多项式回归的原理、应用场景和实现步骤，并通过一个实际案例演示如何使用多项式回归进行预测。

一、原理

多项式回归是一种形式上为多项式的函数与自变量之间的线性回归关系。其基本原理是通过引入高次项来构建一个多项式函数，然后使用最小二乘法或其他优化算法来拟合数据。假设我们的自变量为x，因变量为y，则多项式回归模型可以表示为：

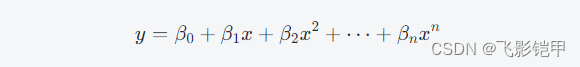
其中，β0,β1,…,βn 是多项式回归模型的系数。通过调整这些系数的值，我们可以改变多项式曲线的形状，从而更好地拟合数据。

二、示例演示

为了更好地理解多项式回归的应用，下面通过一个实际案例来演示如何使用多项式回归进行预测。

假设我们要预测房屋销售价格与其面积之间的关系。首先，我们收集了一组房屋销售数据，包括房屋面积（自变量）和销售价格（因变量）。接下来，我们使用PolynomialFeatures库将面积特征转化为多项式特征。然后，通过线性回归模型拟合多项式特征，并使用训练数据进行训练。最后，我们可以使用训练好的模型来预测新的房屋销售价格。

步骤如下：

数据准备我们需要收集并准备用于训练和测试的数据集。这些数据应该包括自变量（房屋面积）和因变量（销售价格）的数值。
特征工程在应用多项式回归之前，我们需要对自变量进行特征工程，以生成多个高次项。在本例中，我们使用PolynomialFeatures库将面积特征转化为多项式特征。
模型训练接下来，我们将使用线性回归模型来拟合多项式特征，并使用训练数据对模型进行训练。假设我们使用一个二次多项式回归模型，那么该模型可以表示为：

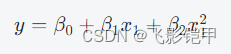
其中，y 表示销售价格， x1 表示房屋面积，β0,β1,β2 是多项式回归模型的系数。我们可以使用最小二乘法或其他优化算法来拟合该模型系数。

模型评估训练完成后，我们需要评估模型的性能。可以使用均方误差（Mean Squared Error）或其他指标来衡量预测结果与实际值之间的差异。
预测最后，我们可以使用训练好的多项式回归模型来进行预测。将新的房屋面积输入模型中，即可得到相应的销售价格预测值。

下面是一个简单的例子，假设我们有以下数据集：

房屋面积（平方米）	销售价格（万元）
50	100
70	120
90	150
110	180
130	200

我们可以使用PolynomialFeatures库将面积特征转化为多项式特征。在这里，我们将使用二次多项式回归模型进行拟合，代码如下：

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 准备训练数据
X_train = [[50], [70], [90], [110], [130]]
y_train = [100, 120, 150, 180, 200]

# 特征工程，生成二次多项式特征
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X_train)

# 模型训练
model = LinearRegression()
model.fit(X_poly, y_train)

# 预测新数据
X_test = [[80], [100]]
X_test_poly = poly.transform(X_test)
y_pred = model.predict(X_test_poly)

print(y_pred)  # 输出预测结果