算法学习——LeetCode力扣二叉树篇3

116. 填充每个节点的下一个右侧节点指针
116. 填充每个节点的下一个右侧节点指针 - 力扣(LeetCode)
描述
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例
示例 1:
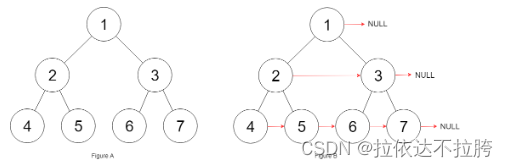
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,‘#’ 标志着每一层的结束。
示例 2:
输入:root = []
输出:[]
提示
- 树中节点的数量在 [0, 212 - 1] 范围内
- -1000 <= node.val <= 1000
进阶
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
代码解析
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
Node* result;
Node* node ; //迭代节点
queue<Node* > my_que; //队列
if(root == nullptr) return root;
else // 根节点进队列
{
my_que.push(root);
}
while(my_que.empty() != 1)
{
int size = my_que.size();
for(int i=0 ; i<size ; i++)
{
node = my_que.front(); //该层级的点弹出放入数组
my_que.pop();
if(i<size-1)//如果该节点不是该层次的最后一个,next指针连接下一个
{
node->next = my_que.front();
}else//该节点是该层次的最后一个,next连接空
{
node->next = nullptr;
}
//每一个弹出点的下一个层级左右节点压入队列
if(node->left != nullptr) my_que.push(node->left);
if(node->right != nullptr) my_que.push(node->right);
}
}
return root;
}
};
117. 填充每个节点的下一个右侧节点指针 II
117. 填充每个节点的下一个右侧节点指针 II - 力扣(LeetCode)
描述
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例
示例 1:
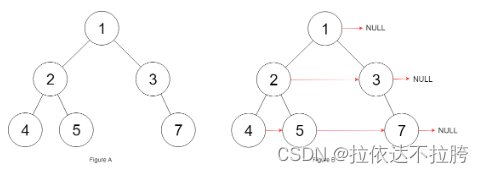
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),‘#’ 表示每层的末尾。
示例 2:
输入:root = []
输出:[]
提示
树中的节点数在范围 [0, 6000] 内
-100 <= Node.val <= 100
进阶
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序的隐式栈空间不计入额外空间复杂度。
代码解析
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> my_que;
if( root == nullptr ) return root;
else my_que.push(root);
while(my_que.size() != 0)
{
int size = my_que.size();
for(int i=0 ; i<size ;i++)
{
Node* tmp_node = my_que.front();
my_que.pop();
if(i == size-1) tmp_node->next = nullptr;
else tmp_node->next = my_que.front();
if(tmp_node->left != nullptr) my_que.push(tmp_node->left);
if(tmp_node->right != nullptr) my_que.push(tmp_node->right);
}
}
return root;
}
};
104. 二叉树的最大深度
104. 二叉树的最大深度 - 力扣(LeetCode)
描述
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示
- 树中节点的数量在 [0, 104] 区间内。
- -100 <= Node.val <= 100
代码解析
层次遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
TreeNode* node ; //迭代节点
queue<TreeNode*> my_que; //队列
int result = 0;
if(root == nullptr) return result;
else // 根节点进队列
{
my_que.push(root);
}
while(my_que.empty() != 1)
{
int size = my_que.size();
result +=1;//计算层级数量
for(int i=0 ; i<size ; i++)
{
node = my_que.front(); //该层级的点弹出放入数组
my_que.pop();
//每一个弹出点的下一个层级左右节点压入队列
if(node->left != nullptr) my_que.push(node->left);
if(node->right != nullptr) my_que.push(node->right);
}
}
return result;
}
};
递归遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getdepth(TreeNode* root)
{
if(root==nullptr) return 0;
int left_depth = getdepth(root->left);
int right_depth = getdepth(root->right);
return 1+max(left_depth , right_depth);
}
int maxDepth(TreeNode* root) {
if(root == nullptr) return 0;
return getdepth(root);
}
};
111. 二叉树的最小深度
111. 二叉树的最小深度 - 力扣(LeetCode)
描述
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示
- 树中节点数的范围在 [0, 105] 内
- -1000 <= Node.val <= 1000
代码解析
层次遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
TreeNode* node ; //迭代节点
queue<TreeNode*> my_que; //队列
int result = 0;
vector<int> min_num;
if(root == nullptr) return result;
else // 根节点进队列
{
my_que.push(root);
}
while(my_que.empty() != 1)
{
int size = my_que.size();
result +=1;
for(int i=0 ; i<size ; i++)
{
node = my_que.front(); //该层级的点弹出放入数组
my_que.pop();
// cout<<node->val<<' '<<node->left<<' '<<node->right<<endl;
//每一个弹出点的下一个层级左右节点压入队列
if(node->left != nullptr) my_que.push(node->left);
if(node->right != nullptr) my_que.push(node->right);
//找到叶子节点
if(node->left == nullptr && node->right == nullptr) min_num.push_back(result);
}
}
//排序找到叶子节点所在最小层
sort(min_num.begin(),min_num.end());
return min_num[0];
}
};
递归法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getdepth(TreeNode* cur)
{
if(cur == nullptr) return 0;
int right_depth , left_depth;
//左子树为空,直接测量右子树
if(cur->left == nullptr && cur->right != nullptr)
{
right_depth = getdepth(cur->right);
return 1 + right_depth;
}else if(cur->left != nullptr && cur->right == nullptr) //右子树为空,直接测量左子树
{
left_depth = getdepth(cur->left);
return 1 + left_depth;
}else//左右子树都为空或都不为空,左右子树均测量,返回最小值
{
left_depth = getdepth(cur->left);
right_depth = getdepth(cur->right);
return 1 + min(left_depth,right_depth);
}
}
int minDepth(TreeNode* root) {
if(root == nullptr) return 0;
return getdepth(root);
}
};