输入位数，求解水仙花数。暴力求解，位数如果太多，会超时。

思路：

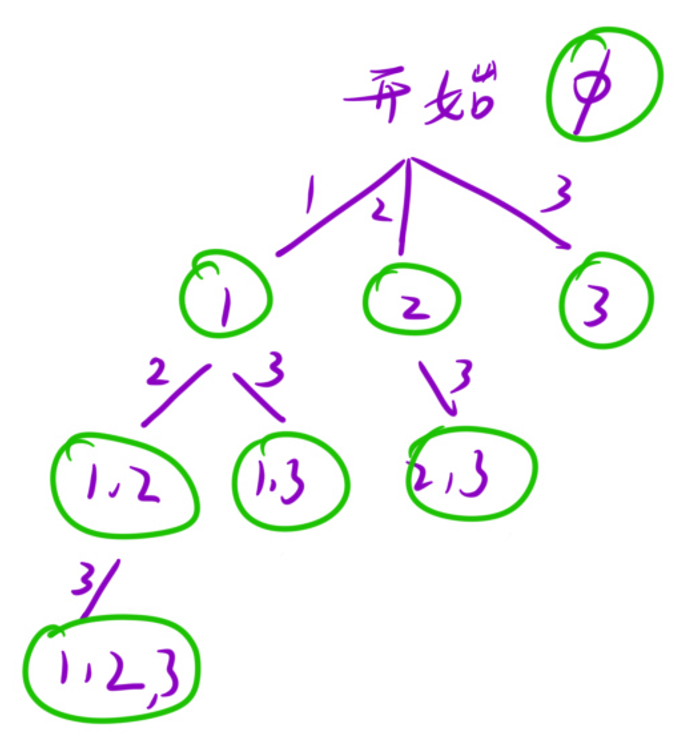
（1）11333355和33331155看上去是不一样的两个数，但是它们又一样，因为相同数字出现的次数一样。

（2）使用递归。每次递归，“统计”这个数中某个数字(cur_digit)出现的次数，直到0-9十个数字全被统计。不断递归的结果，是：“可用”的数字位数(unused_bit)越来越少，与此同时，这个数(cur_sum)也越来越大。当0到9的个数全部统计结束，这个cur_sum就是这个数本身。

运行结果，19位水仙花数有4个，用时0.18秒。如果要求更大的水仙花数，得用biginteger。

程序如下：

#include <iostream>
using namespace std;

void f(int cur_digit, int unused_bit, long long cur_sum);

int n;
long long global_pow[10] = { 0 };
long long min_limit = 1;

int main()
{
	cin >> n;

	clock_t t1 = clock();

	global_pow[1] = 1;
	for (int i = 2; i < 10; i++)
	{
		//计算i^n
		long long _pow = 1;
		for (int j = 0; j < n; j++)
		{
			_pow = _pow * i;
		}
		global_pow[i] = _pow;
	}

	f(0, n, 0);	//cur_digit, unused_bit, cur_sum

	clock_t t2 = clock();
	cout << t2 - t1 << "毫秒" << endl;

	return 0;

}

void f(int cur_digit, int unused_bit, long long cur_sum)
{
	if (unused_bit == 0 || cur_digit == 9)
	{
		cur_sum = cur_sum + unused_bit * global_pow[cur_digit];

		long long temp = cur_sum;
		long long sum = 0;
		int bit_num = 0;
		while (temp)
		{
			int bit = temp % 10;
			sum = sum + global_pow[bit];
			temp = temp / 10;
			bit_num++;
		}
		if (sum == cur_sum && bit_num == n)
		{
			cout << sum << endl;
		}
		return;
	}

	//if (cur_sum < min_limit * 10)
	{
		for (int i = 0; i <= unused_bit; i++)
		{
			f(cur_digit + 1, unused_bit - i, cur_sum + i * global_pow[cur_digit]);
		}
	}
}