适用平台:Matlab2023版本及以上
本程序参考中文EI期刊《电力自动化设备》2023年12月29号网络首发文献:《基于格拉姆角场与并行CNN的并网逆变器开关管健康诊断》,此外,在此基础上进一步对模型进行多重改进,每个人都可以构造属于自己的双流卷积!
文献解读:这篇文献中,首先,采集一维故障电压与电流信号的时序序列;其次,利用格拉姆角场对其进行变换,将两种一维时序信号转化为格拉姆角场,最后,将生成的两组图像同时送入CNN进行并行学习训练,实现逆变器故障诊断。
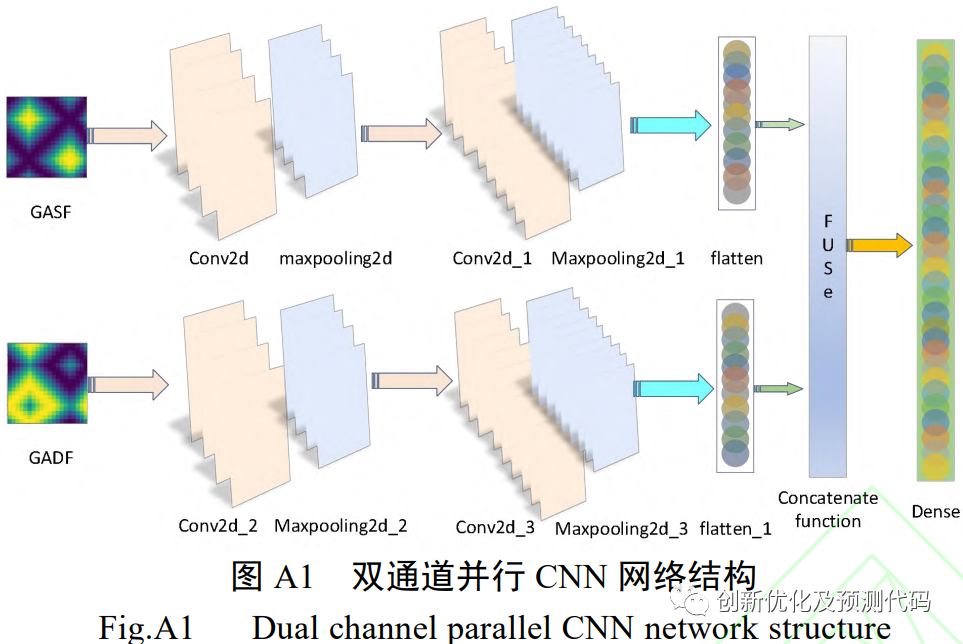
模型改进:我们提出的模型在上述模型基础上作出多重改进:采用双支路结构,构造双流卷积模型(Dual-Stream Convolutional Neural Network,DSCNN),仅需原始故障波形数据,即可根据波形数据,将一维序列转化为二维小波cwt时频图像。①一路为图像输入经2D-CNN提取小波时频图像特征,②另一路为故障波形直接输入1D-CNN提取时序特征,高维图像特征和一维时序特征融合,构建出1D-CNN和2D-CNN(DSCNN)模型。③融合多头注意力机制有效把握提取特征的贡献程度,将特征进行重点强化,提高故障识别的准确率,并计算精确度、召回率、精确率、F1分数等评价指标。故障识别流程如下:
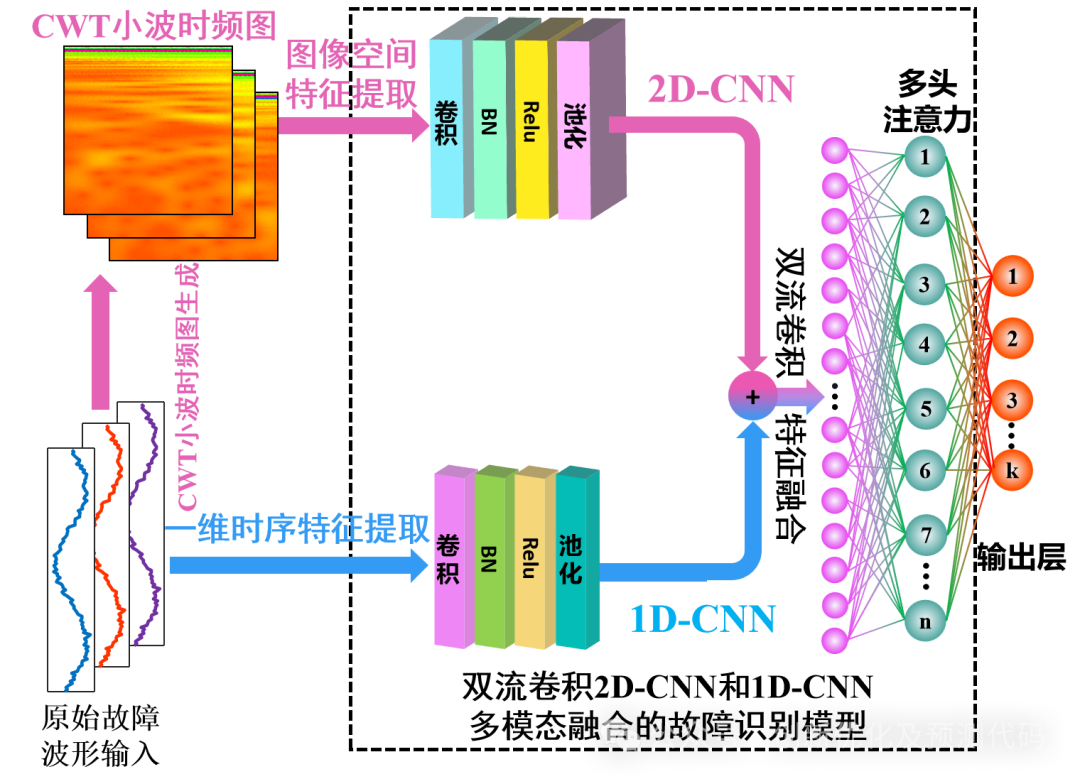
七重创新点:
1、双流卷积:将一维时序信号和二维图像融合,可以综合利用不同模态的信息,从而更全面地描述数据的特征。这有助于提取更丰富、更有区别性的特征,从而提高故障识别的准确性,仅需原始故障波形数据,即可将一维序列转化为二维cwt时频图像。
2、cwt时频特征:cwt时频图提供了时频局部化的特征,可以确定波形在时间和频率上的局部特征。这对于识别故障信号中的瞬态特征或频率成分的突发变化非常有效,这些特征在单一的时域或频域分析中难以分析。
3、波形特征提取:1D-CNN更适合于捕获局部特征和序列中的局部模式。在故障波形中,许多重要的特征可能集中在特定的时间段内,1D-CNN可以更好地捕获这些时间相关的局部特征。
4、空间特征学习:2D-CNN在图像处理中表现出色,能够有效地学习图像的空间特征和局部模式。将2维卷积用于图像数据的处理可以帮助提取图像的纹理、形状和边缘等特征,有助于更准确地进行分类和故障识别。
5、融合优势:通过融合不同模态的信息,算法可以弥补一维时序信号和二维图像各自的局限性。例如,图像可能对于某些故障模式更敏感,而时序信号则对于其他模式更敏感。将它们结合起来,可以增强算法的鲁棒性和泛化能力。
6、多头自注意力机制:融合多头注意力机制有效把握提取特征的贡献程度,将特征进行重点强化,提高故障识别的准确率。
7、提高泛化能力:多模态融合可以帮助算法更好地理解数据的本质特征,从而减少过拟合的风险,提高算法在新数据上的泛化能力。
适用领域:适用于各种数据分类场景,如滚动轴承故障、变压器油气故障、电力系统输电线路故障区域、绝缘子、配网、电能质量扰动,等领域的识别、诊断和分类。
直接替换数据就可以,使用Excel表格直接导入,不需要对程序大幅修改。程序内有详细注释,便于理解程序运行。
数据格式:一行一个样本,最后一列为样本所属的故障类型标签
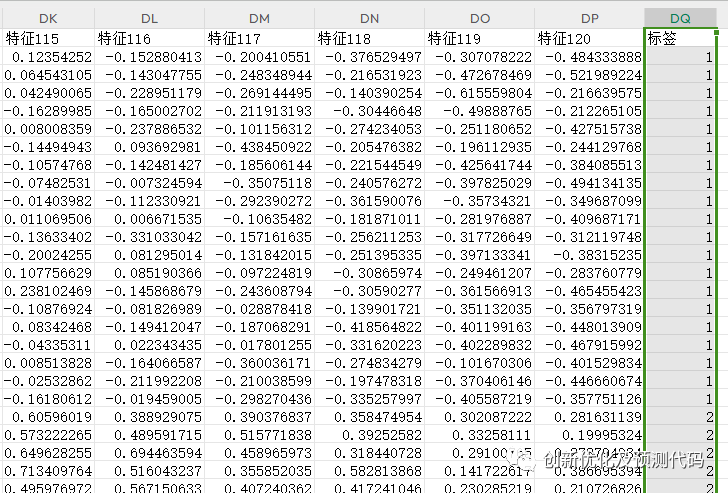
程序结果:(由上述一维序列自动转化为cwt小波时频图像)
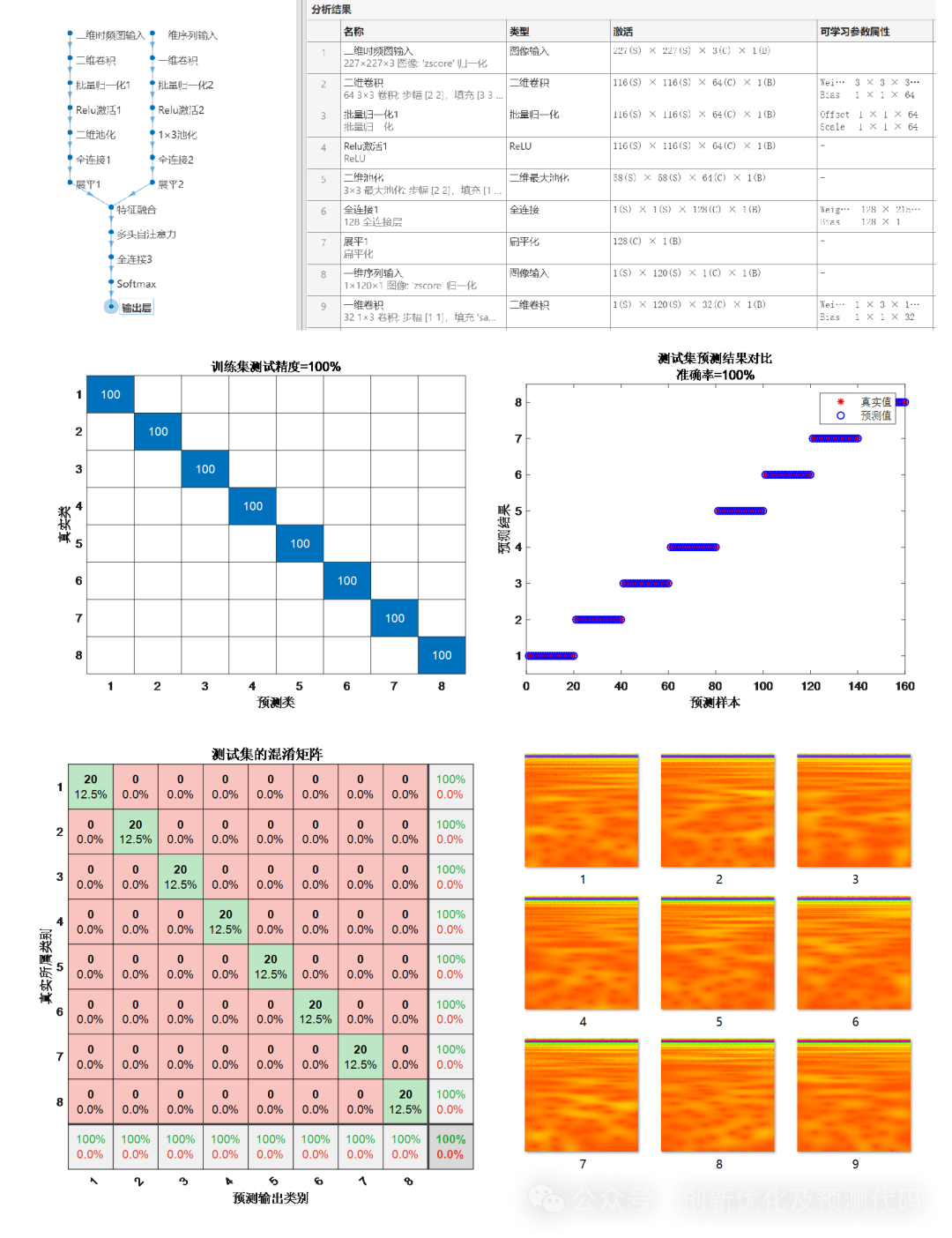
双流模型结构:

训练曲线:
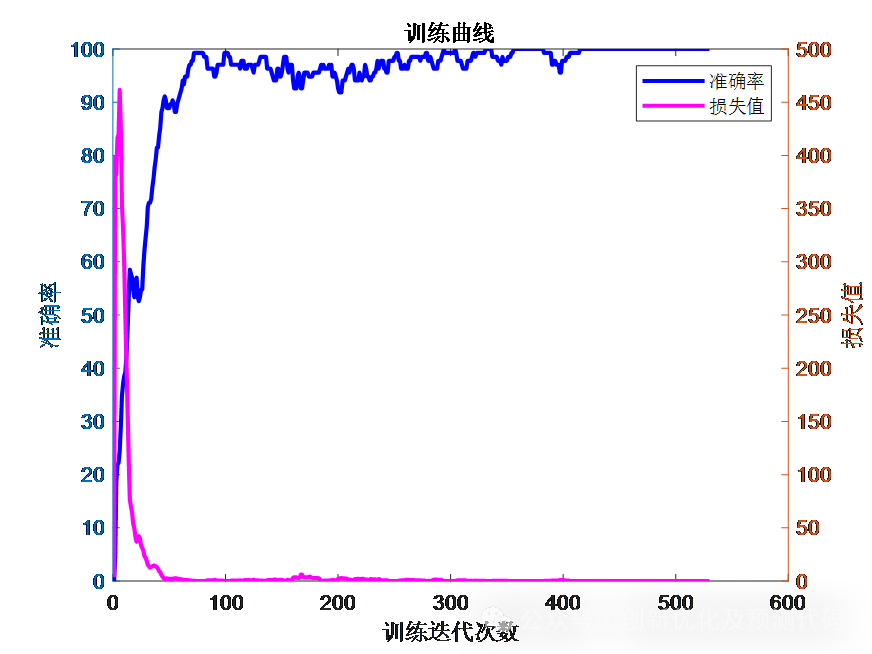
部分图片来源于网络,侵权联系删除!
部分代码:
完整代码:https://mbd.pub/o/bread/ZZqcmphx
%% 构建 Dual-Stream Convolutional Neural Network,DCNN-MSA模型
% 创建层图
lgraph = layerGraph();
% 添加层分支
tempLayers = [
imageInputLayer([227 227 3],"Name","二维时频图输入","Normalization","zscore")
convolution2dLayer([3 3],64,"Name","二维卷积","BiasLearnRateFactor",0,"Padding",[3 3 3 3],"Stride",[2 2])
batchNormalizationLayer("Name","批量归一化1")
reluLayer("Name","Relu激活1")
maxPooling2dLayer([3 3],"Name","二维池化","Padding",[1 1 1 1],"Stride",[2 2])
fullyConnectedLayer(128,"Name","全连接1")
flattenLayer("Name","展平1")];
lgraph = addLayers(lgraph,tempLayers);
tempLayers = [
imageInputLayer([1 120 1],"Name","一维序列输入","Normalization","zscore")
convolution2dLayer([1 3],32,"Name","一维卷积","Padding","same")
batchNormalizationLayer("Name","批量归一化2")
reluLayer("Name","Relu激活2")
averagePooling2dLayer([1 3],"Name","1×3池化","Padding","same")
fullyConnectedLayer(128,"Name","全连接2")
flattenLayer("Name","展平2")];
lgraph = addLayers(lgraph,tempLayers);
tempLayers = [
additionLayer(2,"Name","特征融合")
selfAttentionLayer(1,50,"Name","多头自注意力","NumValueChannels",50,"OutputSize",100)
fullyConnectedLayer(8,"Name","全连接3")
softmaxLayer("Name","Softmax")
classificationLayer("Name","输出层")];
lgraph = addLayers(lgraph,tempLayers);
% 清理辅助变量
clear tempLayers;
% 连接层分支
lgraph = connectLayers(lgraph,"展平1","特征融合/in1");
lgraph = connectLayers(lgraph,"展平2","特征融合/in2");
figure
% 绘制层
plot(lgraph);
string={'双流卷积(DSCNN-MSA)结构'};
title(string)
%% 网络选项
options = trainingOptions('adam', ... % 使用 Adam 优化算法进行训练
'MiniBatchSize',15, ... % 每个小批量的样本数量
'InitialLearnRate',0.001, ... % 初始学习率
'MaxEpochs',10, ... % 最大迭代轮数
'Shuffle','every-epoch', ... % 每轮迭代后重新洗牌训练数据
'Verbose',false, ... % 不在命令行中显示详细信息
'Plots','training-progress'); % 显示训练进度图
analyzeNetwork(lgraph); % 分析网络结构
欢迎感兴趣的小伙伴联系小编或点击代码上方链接获得完整版代码哦~,关注小编会继续推送更有质量的学习资料、文章程序代码~