前言:
傅里叶变换是Modulation, OFDM 技术的理论基础
这里主要介绍连续性随机变量的傅里叶变换,以及对应的性质。
https://zhuanlan.zhihu.com/p/339281545
https://wenku.baidu.com/view/ab338e55a16925c52cc58bd63186bceb19e8ede4.html?_wkts_=1672887094135
https://wenku.baidu.com/view/07613212ccc789eb172ded630b1c59eef8c79acb.html?_wkts_=1672891325952&bdQuery=%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2%E7%9A%84%E5%A5%87%E5%81%B6%E6%80%A7
https://zhuanlan.zhihu.com/p/339281545?ivk_sa=1024320u
目录:
1: 定义
2: 基本性质
3: 常用函数
一 定义
1.1 傅里叶变换
: 时域信号
x(f): 频谱
1.2 傅里叶逆变换
二 性质
2.1 一个域原点的值,是另一域面积
例 f =0 (频域中原点的值)
2.2 线性
假设
则
证明:
2.3 奇偶虚实性
已知
则以下性质成立
2.2.1
2.2.2
设
2.3
当f(t)为偶函数时 f(t)=f(-t)
则 X(w) =0, F(jw)=R(w)
当f(t)为奇函数时 f(t)=-f(-t)
则 R(w) =0, F(jw)=jX(w)
证明:
这里只证明偶函数场景,其它一样
因为
所以
2.4 对称性
f(t) 傅里叶变换为 F(jw)
则 F(jt)的傅里叶变换为
证明:
设 w=t, t=w(只是符号上面的变换)
则
的傅里叶变换为 的傅里叶变换为
2.4 尺度变换性
证明:
设
当a>0
当 a<0
综合得到
2.5 时频特性
Proof:
设 ,则
2.6 时频特性
假设
则
proof:
2.7 卷积特性
这是最重要的性质之一,在解释Modulation ,sample 原理中经常用到
时域的卷积等于频域的乘积
假设
则
证明:
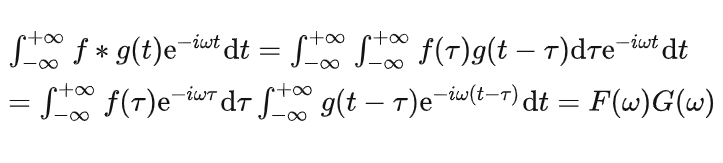
时域的乘积对应频域的卷积
假设
则
证明:
三 常用函数的变换
3.1 1的傅里叶变换
证明:
所以
3.2 矩形脉冲的变换的傅里叶变换
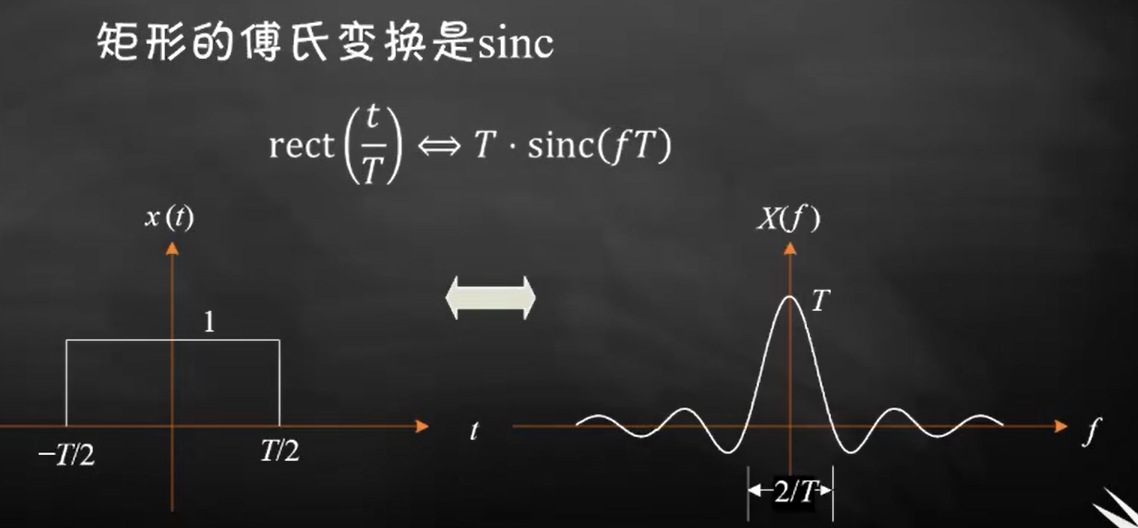
证明:
其中 sinc(x) 定义
在这两种情况下,sinc(0)=1
对于x的所有其他整数值,sinc(x)=0.
3.3 sinc的傅里叶变换为矩形脉冲

证明:
这个要用傅里叶逆变换反过来证明:
这里注意 当使用w 傅里叶逆变换要除以,如果以f 为参数则傅里叶逆变换的标准公式为
则 的傅里叶逆变换为