单调栈题目思路

• 通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)。
• 单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。

单调栈解题步骤

1. 建立一个栈，然后从头遍历元素。
2. 既然为单调栈，那么肯定分为单调递增栈和单调递减栈（这里的单调递增或者递减指的是从栈顶到栈底方向），这里单调栈递增（从栈口到栈底顺序），就是求右边第一个比自己大的，单调栈递减的话，就是求右边第一个比自己小的。 那么分为两种情况：
   • 如果是单调递增栈时，当栈为空或者当前元素值小于栈顶元素时，执行push操作，此时的栈从栈顶到栈底为单调递增，而当前元素值大于栈顶元素值时，不符合单调递增，此时当前元素就是栈顶元素的右侧第一个比它大的元素，输出结果即可（注意这里要循判断栈顶元素是否都符合情况），当然左侧比自己大的元素就是当前栈顶的下一个元素了。
   • 如果是单调递减栈时，同样的思路，当栈为空或者当前元素值大于栈顶元素时，执行push操作，此时的栈从栈顶到栈底为单调递减，而当前元素值小于栈顶元素值时，不符合单调递减，此时当前元素就是栈顶元素的右侧第一个比它小的元素，输出结果即可（注意这里要循判断栈顶元素是否都符合情况），当然左侧比自己小的元素就是当前栈顶的下一个元素了（接雨水和求柱子最大面积会用）。

• 注意：
  • 这里其实在元素等于栈顶元素的时候可以和另一个步骤合并，而不影响计算结果。
  • 单调栈解题，一般都是存数组下标，数组元素可以下标访问，很方便。

每日温度

力扣题目链接
题目描述：
给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:

输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
思路：

• 从题目可以直接看到要求下一个更高温度在几天后，很显然就是求右边第一个比自己大的元素位置减去当前位置下标即位所求，直接使用单调栈来解题，很显然这道题时单调递增栈（从栈顶到栈底）。

代码实现：

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        vector<int> result(temperatures.size(), 0);
        stack<int> stk;
        for (int i = 0; i < temperatures.size(); ++i) {
            while (!stk.empty() && temperatures[i] > temperatures[stk.top()]) {
                int tmp = stk.top();
                result[tmp] = i - tmp;
                stk.pop();
            }
            stk.push(i);
        }
        return result;  
    }
};

下一个最大元素一

力扣题目链接
题目描述：
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：

• 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
• 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
• 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
  示例 2：

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：

• 2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
• 4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

思路：

• 本题和每日温度类似，但是是在另一个数组里找，其实是一样的，我们可以用一个哈希map记录nums1的元素和下标映射关系，然后通过单调栈的方式去找nums2中每个元素的右侧最大值，当遇到符合条件的时候，就到map里找一下是否存在nums2里的这个元素，存在的话，就对应输出即可。

代码实现：

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        vector<int> result(nums1.size(), -1);
        unordered_map<int, int> map;
        for (int i = 0; i < nums1.size(); ++i) {
            map.insert(pair<int, int>{nums1[i], i});
        }
        stack<int> stk;
        for (int i = 0; i < nums2.size(); ++i) {
            //int num = nums2[i];
            while (!stk.empty() && nums2[i] > stk.top()) {
                if (map.count(stk.top())) {
                    result[map[stk.top()]] = nums2[i];
                }
                stk.pop();
            }
            stk.push(nums2[i]);
        }
        return result;
    }
};

下一个最大元素二

力扣题目链接
题目描述：
给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数；
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

思路：

• 和上一个题类似，但是这次是循环数组，那么一般遇到循环数组的时候，我们没必要去把原数组拼接一次，直接让下标可以增长到2*n即可，在访问元素的时候对下标取余操作就不会越界。
• 其他步骤就是单调栈的解题模板，注意这里可以剪枝一下，如果第一轮已经处理过的就不用再push一次了，没处理过的push即可。

代码实现：

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        int n = nums.size();
        stack<int> stk;
        vector<int> result(n, -1);
        for (int i = 0; i < 2 * n; ++i) {//上界为2n时，循环的时候模拟循环数组
            while (!stk.empty() && nums[i % n] > nums[stk.top()]) {
                result[stk.top()] = nums[i % n];
                stk.pop();
            }
            if (result[i % n] == -1) stk.push(i % n);//剪枝，之前已经处理过的可以不用push了。
        }
        return result;
    }
};

接雨水

力扣题目链接
题目描述：
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
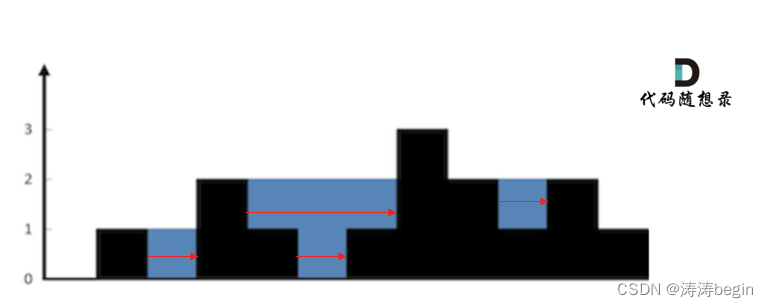
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：
输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

思路：

• 题目解读：若干个柱子，用凹槽去接雨水，这里是去求凹槽的面积之和，有两种思路：

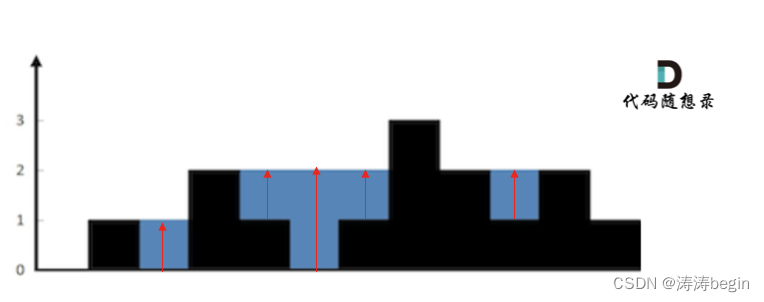
  1. 按列计算（暴力解法），遍历每个元素，求出该元素能接的雨水高度，然后求和，这种情况需要分别求左右两侧比自己高的元素中的最大值，比如下图中的第6列，左侧比自己高的的最高柱子为第4列，右侧是第8列，那么第6列接雨水的高度就是第4列和第8列中高度较小的那个，这里是2。
     

  2. 按行计算（单调栈解法），找出两边第一个比自己高的柱子，然后求出宽度，高度是两边柱子中的最小值减去当前柱子高度，比如还是第6列，此时左右两侧第一个比自己高的是第5和第7列，那么此时宽度就是7 - 5 - 1 = 1，高度是两者的最小值减去第6列的高度：1 - 0 = 1，这里两侧的高度刚好相等了，而如果是第5列的话，那么左右两侧分别是第4和第8列，那么宽度为8 - 4 - 1 = 3，高度为两者的最小值减去第5列的高度：2 - 1 = 1，然后面积就是高度宽度相乘。
     
     代码实现

• 暴力解法（时间复杂度为$O(n^2)$，力扣无法通过）：

class Solution {
public:
    int trap(vector<int>& height) {
        int sum = 0;
        int lhigh = 0, rhigh = 0;
        for (int i = 1; i < height.size() - 1; ++i) {
            //找左边比它大的
            lhigh = height[i], rhigh = height[i];
            for (int j = i - 1; j >= 0; --j) {
                if (height[j] >= lhigh) {//注意这里找的是左边最大的那个，所以一直和lhigh比较
                    lhigh = height[j];
                }
            }
            //找右边比它大的
            for (int k = i + 1; k < height.size(); ++k) {
                if (height[k] >= rhigh) {//注意这里找的是右边最大的那个，所以一直和rhigh比较
                    rhigh = height[k];
                }
            }
            sum += min(rhigh, lhigh) - height[i];
        }
        return sum;
    }
};

• 暴力解法优化：其实在找左右两侧最大值的时候有很多重复比较，我们其实直接取前面一个元素的结果和当前值做比较即可（（为什么和当前值比较？如果没有比自己大的，就用当前值，那么算的时候高度差为0，就没有高度无法接雨水了）），在遍历数组之前，先把左右两侧比自己高的最大值找出来。

class Solution {
public:
    int trap(vector<int>& height) {
        int sum = 0;
        vector<int> l_max_vec(height.size(), 0);
        vector<int> r_max_vec(height.size(), 0);
        //直接把每个位置的左侧最高柱子都计算出来
        l_max_vec[0] = height[0];
        for (int i = 1; i < height.size(); ++i) {
            l_max_vec[i] = max(l_max_vec[i - 1], height[i]);
        }
        //直接把每个位置的右侧最高柱子都计算出来
        r_max_vec[height.size() - 1] = height[height.size() - 1];
        for (int j = height.size() - 2; j >= 0; --j) {
            r_max_vec[j] = max(r_max_vec[j + 1], height[j]);
        }
        //循环一次，直接计算即可。
        for (int i = 1; i < height.size() - 1; ++i) {  
            sum += min(l_max_vec[i], r_max_vec[i]) - height[i];
        }
        return sum;
    }
};

• 单调栈解法（按行求解）：

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk;
        int sum = 0;
        for (int i = 0; i < height.size(); ++i) {
            while (!stk.empty() && height[i] > height[stk.top()]) {
                int cur = stk.top();
                stk.pop();
                if (stk.empty())   break;
                int next = stk.top();//前面比它高的
                int high = min(height[i], height[next]) - height[cur];//高度差
                int weight = i - next - 1;//宽度
                sum += high * weight;//面积
            }
            stk.push(i);/*这里可以剪枝，如果相邻两个柱子高度相同算一个就行了，因为即使放进去，
                        high计算的时候也是0*/
        }
        return sum;
    }
};

柱状图中最大的矩形

力扣题目链接
题目描述：
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

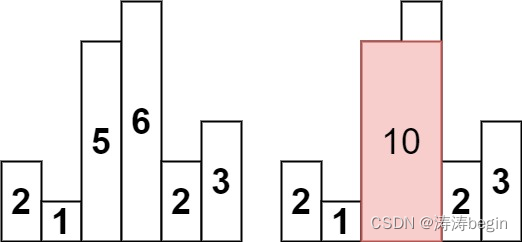
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

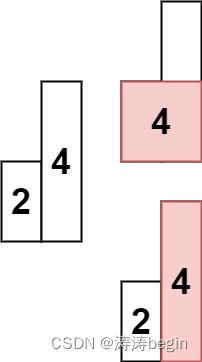
输入： heights = [2,4]
输出： 4

思路：

• 和接雨水类似，但是本题更加复杂，接雨水是求凹槽，相当于是柱子外，本题是求柱子内的最大面积，**既然是求最大面积，那么本题需要找到的是每个柱子的左右两侧的第一个比自己小的那个柱子（注意这个题和前面四道题不一样了！！！，是求左右两侧比自己小的柱子，此时为栈顶到栈底单调递减），**这样的话用得到的宽度和当前柱子高度相乘即为已当前柱子为高度的矩形面积，然后依次对每个柱子求矩形面积取最大值即可。
• 暴力解法：和接雨水不太一样，本题是找到左右两侧第一个比自己小的柱子（不再是找最小的柱子了（接雨水是找最大的柱子））
• 注意：
  • 如果数组本身单调递增的话，那么入栈后整体呈现单调递减就找不到右侧比自己小的元素了，这种情况对于接雨水来说不用特殊处理（没有凹槽，雨水为0），但是本题不行，可以直接在原数组尾部加一个0，这样既不影响结果，也能找到了右侧比自己小的元素。
  • 对于数组单调递减的情况不用在数组开头添加元素，直接让left的高度设为-1即可。

代码实现

• 单调栈解法：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = 0;
        stack<int> stk;
        heights.push_back(0);//单独处理，尾部加0
        for (int i = 0; i < heights.size(); ++i) {
            while (!stk.empty() && heights[i] < heights[stk.top()]) {
                int top = stk.top();
                stk.pop();
                int left = -1;//单独处理，left设为-1
                if (！stk.empty())    left = stk.top();
                int weight = i - left - 1;
                int s = heights[top] * weight;
                result = max(result, s);
            }
            stk.push(i);
        }
        return result;
    }
};

• 暴力解法：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = INT_MIN;
        for (int i = 0; i < heights.size(); ++i) {
            int l_min = -1, r_min = heights.size();
            for (int j = i - 1; j >= 0; --j) {
                if (heights[j] < heights[i]) {
                    l_min = j;
                    break;
                }
            }
            for (int k = i + 1; k < heights.size(); ++k) {
                if (heights[k] < heights[i]) {
                    r_min = k;
                    break;
                }  
            }
            //cout << l_min << " " << r_min << endl;
            int weight = r_min - l_min - 1;
            int s = weight * heights[i];
            result = result > s ? result : s;
        }
        return result;
    }
};

• 暴力解法优化：和接雨水优化类似，但是此处需要在for循环里用while循环去不断找到小于cur的柱子。（注意遇到等于的时候也要继续去找,当然也可以把等于逻辑拿出来单独写，其实是一样的）

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = INT_MIN;
        vector<int> l_min_vec(heights.size(), -1);//默认没有比当前柱子小的
        vector<int> r_min_vec(heights.size(), heights.size());//默认没有比当前柱子小的
        //求左侧第一个小于当前高度的柱子
        for (int i = 1; i < heights.size(); ++i) {
            int t = i - 1;
            while (t >= 0 && heights[t] >= heights[i]) {
                t = l_min_vec[t];
            }//大于一直往左走
            l_min_vec[i] = t;//直到遍历到头或者小于的时候
        }
        //求右侧第一个小于当前高度的柱子
        for (int j = heights.size() - 2; j >= 0; --j) {
            int t = j + 1;
            while (t < heights.size() && heights[t] >= heights[j]) {
                t = r_min_vec[t];
            }//大于等于一直往右走
            r_min_vec[j] = t;//直到遍历到头或者小于的时候
        }
        //求面积
        for (int i = 0; i < heights.size(); ++i) {
            int weight = r_min_vec[i] - l_min_vec[i] - 1;
            int s = weight * heights[i];
            result = max(s, result);
        }
        return result;
    }
};

总结

• 单调栈题目大体模版都是一样的，就是while里的处理逻辑可能不同，可以先熟悉暴力解法，然后看看和单调栈解法的区别在哪，妙在哪里。