文章目录
- 摘要
- 1、简介
- 2、相关工作
- 2.1、视觉Transformers
- 2.2、ViT时代的卷积网络
- 3、从多阶博弈论交互的角度看表示瓶颈
- 4、方法论
- 4.1、MogaNet概述
- 4.2、多阶门控聚合
- 4.3、通过通道聚合进行多阶特征重新分配
- 4.4、实现细节
- 5、实验
- 5.1、ImageNet分类
- 5.2、密集预测任务
- 5.3、消融实验和分析
- 6、结论
- 致谢
- A、实现细节
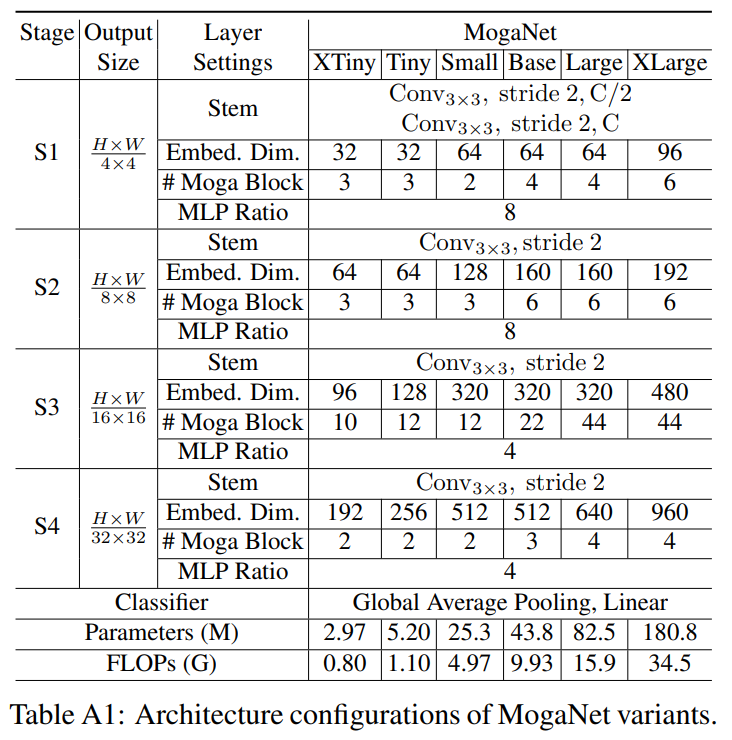
- A.1、架构细节
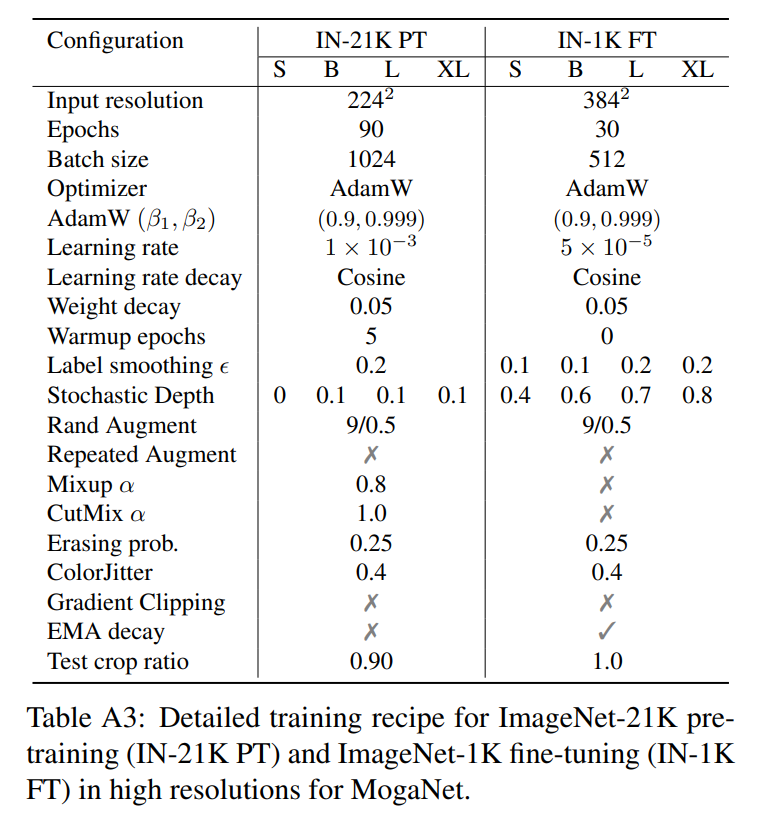
- A.2、ImageNet实验设置
- A.3、COCO上的目标检测和实例分割
- A.4、ADE20K上的语义分割
- A.5、COCO上的2D人体姿态估计
- A.6、3D人体姿态估计
- A.7、移动MNIST上的视频预测
- B、实验结果
- B.1、DNNs的表示瓶颈:多阶交互视角
- C、更多消融和分析结果
- C.1、激活函数的消融
- C.2、多阶DWConv层的消融
- C.3、MogaNet 的 FLOPs 和吞吐量
- C.4、归一化层的消融研究
- C.5、轻量级模型的优化训练设置
- D、更多对比实验
- D.1、在ImageNet-1K上的快速训练
- D.2、在COCO上的检测和分割结果
- D.3、ADE20K上的语义分割结果
- D.4、COCO上的2D人体姿态估计结果
- D.5、3D人体姿态估计结果
- D.6、Moving MNIST上的视频预测结果
摘要
https://arxiv.org/pdf/2211.03295.pdf
在这项工作中,我们从多阶博弈论交互这一全新视角探索了现代卷积神经网络的表示能力。这种交互反映了不同尺度上下文中变量间的相互作用效果。在现代卷积神经网络框架中,我们定制了两个特征混合器,它们采用概念上简单但高效的深度卷积,以促进空间和通道空间中的中等阶信息。因此,我们提出了一种新的纯卷积神经网络架构族,称为MogaNet。MogaNet具有出色的可扩展性,在ImageNet和其他多种典型视觉基准测试中,与最先进的模型相比,其参数使用更高效,且具有竞争力的性能。具体来说,MogaNet在ImageNet上实现了80.0%和87.8%的Top-1准确率,分别使用了5.2M和181M参数,优于ParC-Net-S和ConvNeXt-L,同时节省了59%的浮点运算和17M的参数。源代码可在GitHub上(https://github.com/Westlake-AI/MogaNet)获取。
1、简介
自深度神经网络(DNNs)复兴以来,卷积神经网络(ConvNets)已成为计算机视觉领域的首选方法。通过在池化和非线性操作之间交替使用层次化的卷积层,ConvNets能够利用内置的平移等变约束来编码观察图像的底层语义模式,并进一步成为当今计算机视觉系统中的基础设施。然而,ConvNets所学习的表示对局部纹理有很强的偏见,这导致全局信息的严重损失。因此,研究者们一直在努力改进宏观层次架构和上下文聚合模块。
相比之下,通过放松局部归纳偏置,新出现的Vision Transformers(ViTs)在各种视觉基准测试中迅速挑战了ConvNets的长期统治地位。几乎一致的共识是,ViTs的这种优越性主要源于自注意力机制,它促进了长期特征交互,而与拓扑距离无关。然而,从实际角度来看,自注意力建模中的二次复杂性严重限制了ViTs的计算效率,及其在需要高分辨率特征的精细场景中的应用潜力。此外,缺乏归纳偏置会破坏图像的内在几何结构,从而不可避免地导致邻域相关性受到损害。为了解决这一障碍,人们做出了努力,重新引入了金字塔式的层次布局和移位不变先验,以牺牲模型通用性和表现力为代价。
最近的研究表明,ViTs的表现能力主要归功于其宏观层次架构,而不是通常推测的自注意力机制。更重要的是,通过先进的训练设置和ViT风格的架构现代化,ConvNets可以轻松地提供出色的可扩展性和竞争力,与经过良好调整的ViTs在各种视觉基准测试中相比。这加剧了ConvNets和ViTs之间的争论,并进一步改变了深度架构设计的路线图。
与之前的尝试不同,我们通过多阶博弈论交互的视角来研究现代ConvNets的表现能力,这为基于博弈论的深度架构中的特征交互行为和效果提供了一个新的解释视角。如图3b所示,大多数现代DNNs倾向于编码极低或极高复杂性的博弈论交互,而不是最具辨别力的中间复杂性,这限制了它们的表示能力和对复杂样本的鲁棒性。
从这一角度来看,我们开发了一种新型的纯ConvNet架构,称为多阶门控聚合网络(MogaNet),以平衡多阶交互强度,从而提高ConvNets的性能。我们的设计将低阶局部先验和中等阶上下文聚合封装到一个统一的空间聚合块中,其中平衡的多阶交互特征通过门控机制并行地聚集和上下文化。从通道方面来看,由于现有方法容易产生通道信息冗余[104, 61],我们定制了一个概念简单但高效的通道聚合块,它对多阶输入进行自适应通道特征重新分配,并以较低的计算成本显著优于现有的同类方法(例如SE模块[60])。
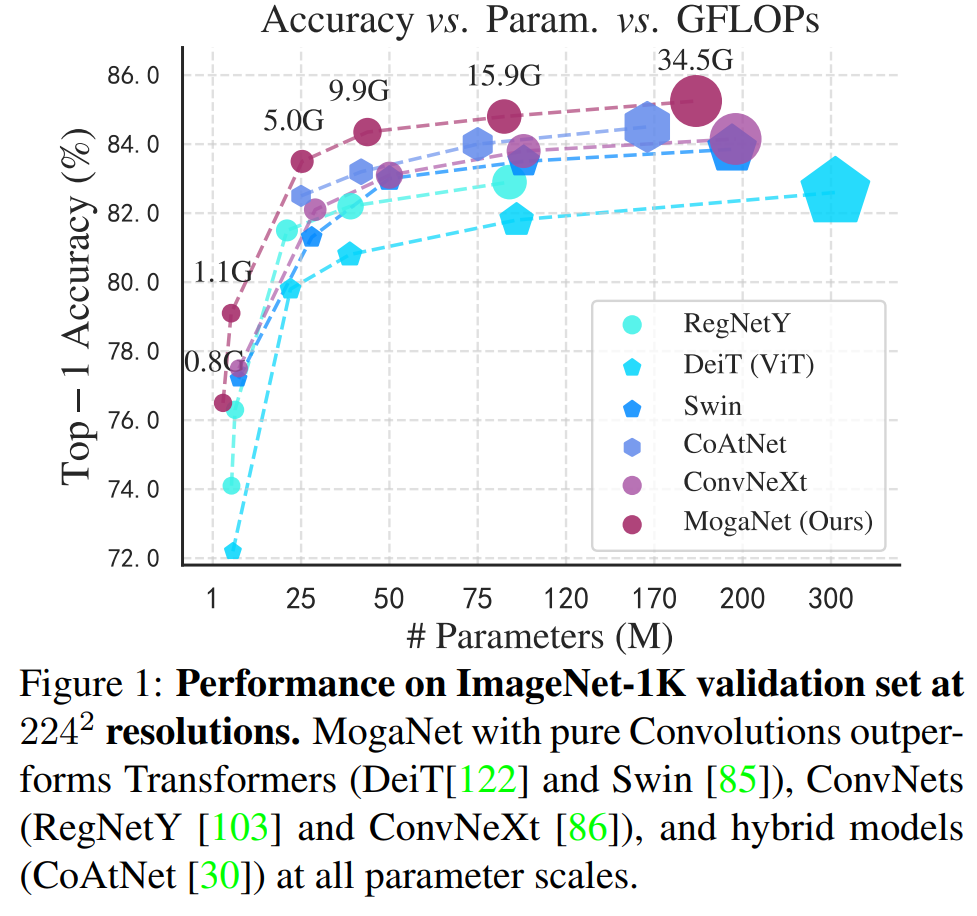
大量的实验证明了MogaNet在不同模型规模和各种计算机视觉任务中的出色性能和效率,包括图像分类、目标检测、语义分割、实例分割、姿态估计等。因此,如图1所示,MogaNet在25M和181M参数下分别达到了83.4%和87.8%的准确率,与现有的小型模型相比,显示出有利的计算开销。在相同的设置下,MogaNet-T在ImageNet-1K上实现了80.0%的top-1准确率,比最先进的ParCNet-S[161]高出1.0%,同时降低了2.04G的FLOPs。此外,MogaNet在各种下游任务上表现出强劲的性能提升,例如,在COCO检测上,以更少的参数和计算预算超过了Swin-L[85]的2.3%的APb。因此,MogaNet的性能提升并不是由于容量的增加,而是由于更有效地利用了模型参数。
2、相关工作
2.1、视觉Transformers
Transformer在自然语言处理(NLP)中取得了显著的成就[35, 10],因此Vision Transformer(ViT)被提出,并在ImageNet上取得了令人鼓舞的结果[34]。然而,与ConvNets相比,纯ViTs过度参数化,并依赖于大规模预训练[38,7,51,75]。针对这一问题,一些研究人员提出了轻量级的ViTs[147, 93, 77, 18],并开发了高效的自注意力变体[134]。同时,将自注意力和卷积作为混合主干进行研究的课题也得到了广泛研究[47, 141,30,31,72,96,111],以便为ViTs提供区域先验。通过引入归纳偏差[14, 168, 16, 98, 65, 3]、先进的训练策略[122, 123, 155, 125]或额外知识[66, 78, 143],ViT及其变种可以与ConvNets竞争,并扩展到各种计算机视觉领域。
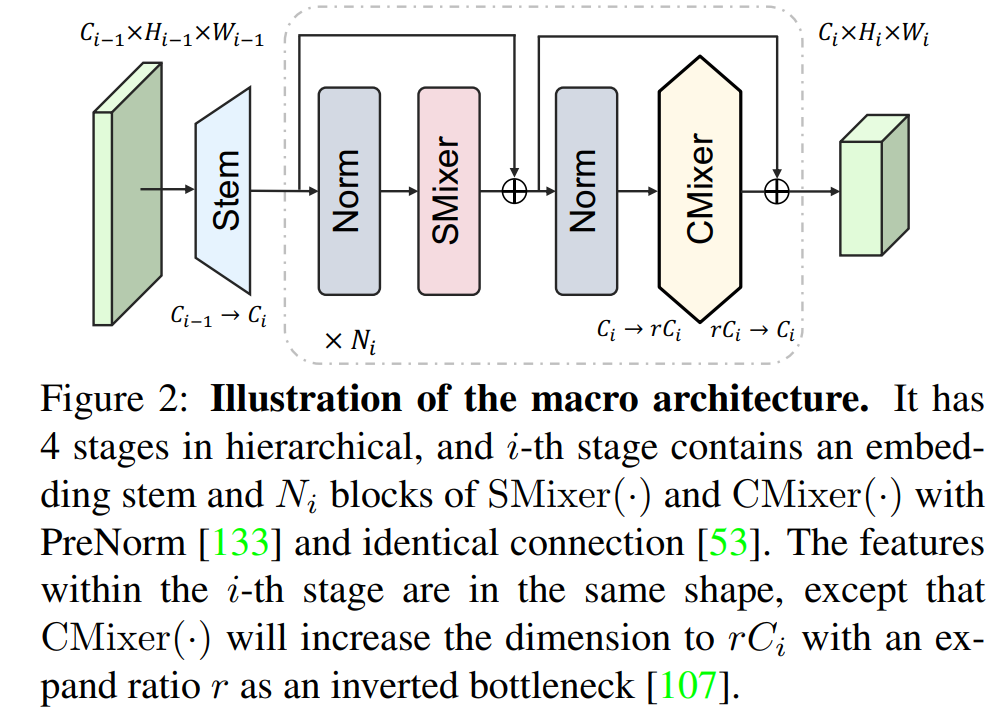
MetaFormer[154]如图2所示,对深层架构设计原则产生了重大影响,其中所有ViTs[122,127,130]可以根据如何处理令牌混合方法进行分类,例如相对位置编码[142],局部窗口移动[85]和MLP层[121]等。它主要包括三个基本组件:(i)嵌入stem,(ii)空间混合块,和(iii)通道混合块。嵌入stem对输入图像进行下采样,以减少图像固有的冗余和计算过载。假设输入特征X和输出Z具有相同的形状
R
C
×
H
×
W
\mathbb{R}^{C \times H \times W}
RC×H×W,我们有:
Z
=
Stem
(
X
)
,
Z=\operatorname{Stem}(X),
Z=Stem(X),
其中Z是下采样特征,例如。然后,特征流到一系列残差块中。在每个阶段,网络模块可以分解为两个独立的功能组件,
SMixer
(
⋅
)
和
CMixer
(
⋅
)
\operatorname{SMixer}(\cdot)和\operatorname{CMixer}(\cdot)
SMixer(⋅)和CMixer(⋅),用于空间信息和通道信息的传播[154],
Y
=
X
+
SMixer
(
Norm
(
X
)
)
,
Y=X+\operatorname{SMixer}(\operatorname{Norm}(X)),
Y=X+SMixer(Norm(X)),
Z
=
Y
+
CMixer
(
Norm
(
Y
)
)
,
Z=Y+\operatorname{CMixer}(\operatorname{Norm}(Y)),
Z=Y+CMixer(Norm(Y)),
其中
Norm
(
⋅
)
\operatorname{Norm}(\cdot)
Norm(⋅)是一个归一化层,例如批量归一化[63](BN)。请注意,
SMixer
(
⋅
)
\operatorname{SMixer}(\cdot)
SMixer(⋅)可以是各种空间操作(例如自注意力[129]、卷积),而
C
M
i
x
e
r
(
⋅
)
CMixer(\cdot)
CMixer(⋅)通常通过通道-wise MLP在倒瓶颈[107]中实现,并具有扩展比r。
2.2、ViT时代的卷积网络
现代ConvNets通过利用ViT风格宏观架构的优点,使用大深度卷积进行全局上下文聚合,表现出了激动人心的性能。类似于ViTs,现代ConvNets中的上下文聚合操作可以总结为一组组件,这些组件能够自适应地强调上下文信息,并减少两个嵌入特征之间空间混合中的冗余。
O
=
S
(
F
ϕ
(
X
)
,
G
ψ
(
X
)
)
,
O=\mathcal{S}\left(\mathcal{F}_{\phi}(X), \mathcal{G}_{\psi}(X)\right),
O=S(Fϕ(X),Gψ(X)),
其中
F
ϕ
(
⋅
)
和
G
ψ
(
⋅
)
\mathcal{F}_{\phi}(\cdot)和\mathcal{G}_{\psi}(\cdot)
Fϕ(⋅)和Gψ(⋅)是聚合分支和上下文分支,分别具有参数
ϕ
\phi
ϕ和
ψ
\psi
ψ。上下文聚合通过聚合分支
F
ϕ
(
X
)
\mathcal{F}_{\phi}(X)
Fϕ(X)来模型X中每个位置的重要性,并通过权重函数
S
(
⋅
,
⋅
)
\mathcal{S}(\cdot, \cdot)
S(⋅,⋅)对上下文分支
G
ψ
(
X
)
\mathcal{G}_{\psi}(X)
Gψ(X)的嵌入特征进行重新加权。
如表1所示,现代ConvNets中的上下文聚合主要有两种类型:自注意力机制[129, 137, 38]和门控注意力[32, 60]。在
F
ϕ
(
⋅
)
\mathcal{F}_{\phi}(\cdot)
Fϕ(⋅)中,通过所有其他位置与X中每个位置的点积进行全局交互来计算每个位置的重要性,这导致计算复杂度为二次。为了克服这一限制,提出了线性复杂度的注意力变体[90,102],以替换原始的自注意力,例如表1中的第二行的线性注意力[134, 95],但它们可能会退化为简单的注意力[140]。与自注意力不同,门控单元使用元素乘积
⊙
\odot
⊙作为线性复杂度中的
S
(
⋅
,
⋅
)
\mathcal{S}(\cdot, \cdot)
S(⋅,⋅),例如表1中最后两行的门控线性单元(GLU)变体[109]和挤压-激励(SE)模块[60]。

3、从多阶博弈论交互的角度看表示瓶颈
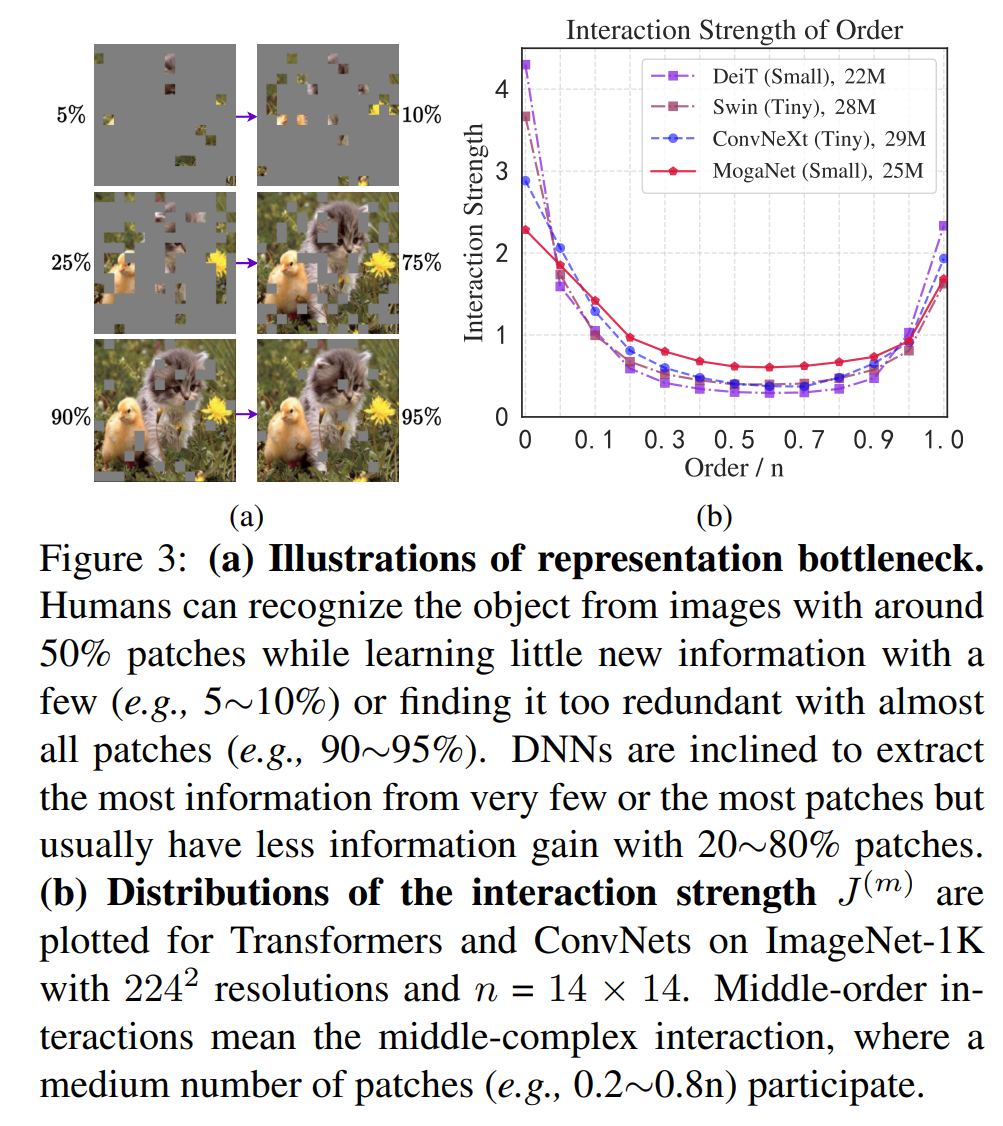
最近对DNN的鲁棒性[94, 166, 97]和泛化能力[44,2,128,43]的分析为改进深度架构提供了新的视角。除了这些努力,我们将研究范围扩展到多阶博弈论交互。如图3a所示,DNN在极端遮挡比例(例如只有10-20%的可见补丁)下仍然可以识别目标对象,但产生较少的信息增益[33, 94]。有趣的是,我们的大脑在大约50%的补丁图像中获得最清晰的知识增长,这表明人类视觉和深度模型之间存在有趣的认知差距。正式地说,这可以通过m阶博弈论交互
I
(
m
)
(
i
,
j
)
I^{(m)}(i, j)
I(m)(i,j)和
m
m
m阶交互强度
J
(
m
)
J^{(m)}
J(m)来解释,如[162,33]所定义。考虑总共有n个补丁的图像,
I
(
m
)
(
i
,
j
)
I^{(m)}(i, j)
I(m)(i,j)测量在由m个补丁组成的所有上下文中,补丁对i和j之间的平均交互复杂性,其中
0
≤
m
≤
n
−
2
0≤m≤n-2
0≤m≤n−2,并且
m
m
m阶反映像素
i
i
i和
j
j
j之间的博弈论交互中涉及的上下文尺度。通过交互强度的平均值进行归一化,相对交互强度
J
(
m
)
J^{(m)}
J(m)在
m
∈
(
0
,
1
)
m∈(0,1)
m∈(0,1)中测量DNN中编码的交互复杂性。值得注意的是,低阶交互倾向于编码常见的或广泛共享的局部纹理,而高阶交互倾向于强行记忆稀有异常值的模式[33, 20]。请参阅附录B. 1以获取定义和详细信息。如Fig. 3b所示,大多数DNN更倾向于编码过度的低阶或高阶博弈论交互,而通常抑制最具灵活性和区分性的中间阶交互[33,20]。从我们的角度来看,卷积神经网络和视觉Transformer中的这种困境可能归因于卷积诱导偏差和上下文聚合的不当组合[126,128,33,75]。特别是,对自注意力或卷积的简单实现可能容易受到全局形状的强烈偏见[43,36]或局部纹理[56],将错误的极端阶博弈论交互偏好注入深度网络。
4、方法论
4.1、MogaNet概述
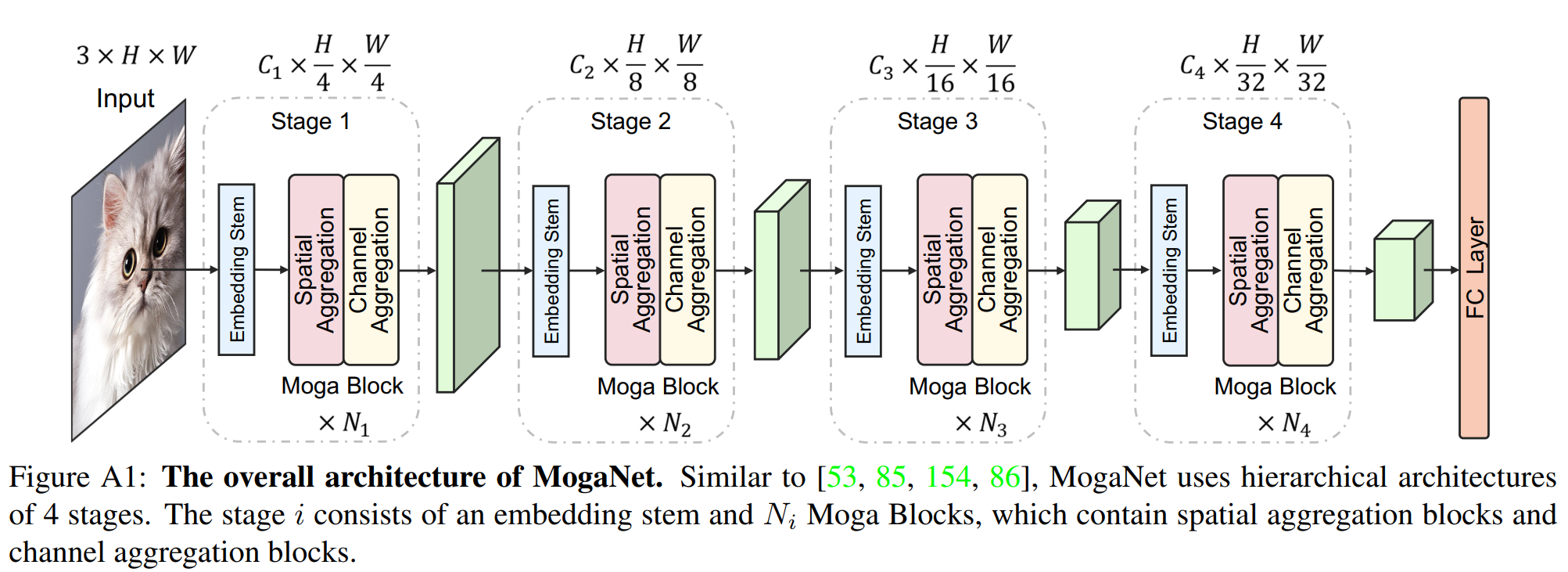
根据图2,我们设计了MogaNet的四级架构,如图A1所示。对于第i阶段,首先将输入图像或特征送入嵌入主干,以调节特征分辨率并将其嵌入到C_{i}维度。假设输入图像的分辨率为H×W,四个阶段的特征分辨率为 H / 4 × W / 4 H/4×W/4 H/4×W/4、 H / 8 × W / 8 H/8×W/8 H/8×W/8、 H / 16 × W / 16 H/16×W/16 H/16×W/16和 H / 32 × W / 32 H/32×W/32 H/32×W/32。然后,嵌入的特征流经 N i N_{i} Ni个Moga块,这些块由空间和通道聚合块组成,如第4.2和4.3节所述,用于进一步的上下文提取和聚合。最后添加全局平均池化层和一个线性层进行分类任务。对于密集预测任务[52, 146],可以通过颈部模块[79, 69]使用四个阶段的输出。
4.2、多阶门控聚合
如第3节所述,具有本地感知和上下文聚合之间不兼容组合的传统深度神经网络容易过度关注极端阶交互,而抑制最具辨别力的中间阶交互[72, 100, 33]。如图5所示,主要的挑战是如何高效地捕获具有平衡多阶博弈论交互的上下文表示。为了解决这个问题,我们提出了一种空间聚合(SA)块作为SMixer(.),以统一设计聚合多阶上下文,如图4所示,该块由两个串联组件组成。我们将等式(2)重写为:
Z
=
X
+
Moga
(
FD
(
Norm
(
X
)
)
)
,
Z=X+\operatorname{Moga}(\operatorname{FD}(\operatorname{Norm}(X))),
Z=X+Moga(FD(Norm(X))),
其中,
F
D
(
⋅
)
\mathrm{FD}(\cdot)
FD(⋅)表示特征分解模块(FD),
M
o
g
a
(
⋅
)
Moga (\cdot)
Moga(⋅)是一个多阶门控聚合模块,包括门控函数
F
ϕ
(
⋅
)
\mathcal{F}_{\phi}(\cdot)
Fϕ(⋅)和上下文分支
G
ψ
(
⋅
)
\mathcal{G}_{\psi}(\cdot)
Gψ(⋅)。
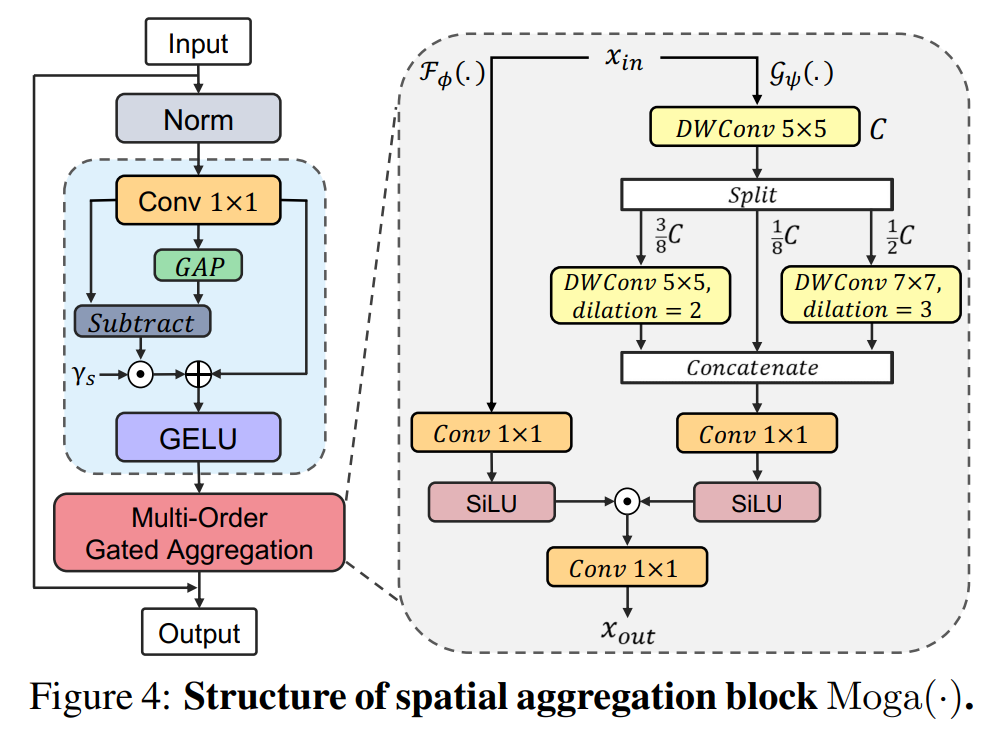
多阶上下文。作为一种纯粹的卷积结构,我们通过静态和自适应区域感知来提取多阶特征。除了m阶交互之外,还有两个互补的对应物,即覆盖复杂全局形状的0阶交互和’n阶’交互,分别由 Conv 1 × 1 ( ⋅ ) \operatorname{Conv}_{1 \times 1}(\cdot) Conv1×1(⋅)和 GAP ( ⋅ ) \operatorname{GAP}(\cdot) GAP(⋅)表示。为了迫使网络专注于平衡多复杂性的交互,我们提出 F D ( ⋅ ) \mathrm{FD}(\cdot) FD(⋅)来动态排除平凡的特征交互,定义如下:
Y
=
Conv
1
×
1
(
X
)
,
Z
=
GELU
(
Y
+
γ
s
⊙
(
Y
−
GAP
(
Y
)
)
)
,
\begin{array}{l} Y=\operatorname{Conv}_{1 \times 1}(X), \\ Z=\operatorname{GELU}\left(Y+\gamma_{s} \odot(Y-\operatorname{GAP}(Y))\right), \end{array}
Y=Conv1×1(X),Z=GELU(Y+γs⊙(Y−GAP(Y))),
其中,
γ
s
∈
R
C
×
1
\gamma_{s} \in \mathbb{R}^{C \times 1}
γs∈RC×1表示一个初始化为零的缩放因子。通过重新加权互补交互组件
Y
−
GAP
(
Y
)
Y-\operatorname{GAP}(Y)
Y−GAP(Y),
FD
(
⋅
)
\operatorname{FD}(\cdot)
FD(⋅)还可以增加空间特征的多样性[97, 132]。然后,我们将深度卷积(DWConv)集成到Moga(⋅)的上下文分支中,以编码多阶特征。与之前将DWConv与自注意力简单结合以模拟局部和全局交互的工作不同[161, 95, 111, 105],我们并行使用了三个具有不同膨胀比
d
∈
{
1
,
2
,
3
}
d \in\{1,2,3\}
d∈{1,2,3}的DWConv层,以捕获低、中、高阶交互:给定输入特征
X
∈
R
C
×
H
W
X \in \mathbb{R}^{C \times H W}
X∈RC×HW,首先应用
D
W
5
×
5
,
d
=
1
\mathrm{DW}_{5 \times 5, d=1}
DW5×5,d=1,以提取低阶特征;然后,将输出分解为
X
l
∈
R
C
l
×
H
W
,
X
m
∈
R
C
m
×
H
W
,
X
h
∈
R
C
h
×
H
W
X_{l} \in \mathbb{R}^{C_{l} \times H W}, X_{m} \in \mathbb{R}^{C_{m} \times H W}, X_{h} \in \mathbb{R}^{C_{h} \times H W}
Xl∈RCl×HW,Xm∈RCm×HW,Xh∈RCh×HW,其中
C
l
+
C
m
+
C
h
=
C
C_{l} + C_{m} + C_{h} = C
Cl+Cm+Ch=C;之后,将
X
m
X_{m}
Xm和
X
h
X_{h}
Xh分别分配给
D
W
5
×
5
,
d
=
2
\mathrm{DW}_{5 \times 5, d=2}
DW5×5,d=2和
D
W
7
×
7
,
d
=
3
\mathrm{DW}_{7 \times 7, d=3}
DW7×7,d=3,而
X
l
X_{l}
Xl作为恒等映射;最后,将
X
l
X_{l}
Xl、
X
m
X_{m}
Xm和
X
h
X_{h}
Xh的输出连接起来形成多阶上下文,
Y
C
=
Concat
(
Y
l
,
1
:
C
l
,
Y
m
,
Y
h
)
Y_{C}=\operatorname{Concat}\left(Y_{l, 1: C_{l}}, Y_{m}, Y_{h}\right)
YC=Concat(Yl,1:Cl,Ym,Yh)。请注意,与ConvNeXt中使用的
D
W
7
×
7
\mathrm{DW}_{7 \times 7}
DW7×7相比,所提出的
F
D
(
⋅
)
\mathrm{FD}(\cdot)
FD(⋅)和多阶DWConv层仅需要稍微增加一些计算开销和参数,如表2所示。例如,+multi-order和
+
F
D
(
⋅
)
+\mathrm{FD}(\cdot)
+FD(⋅)增加了0.04M参数和0.01G FLOPS。

门控聚合。为了从上下文分支聚合多阶特征,我们在门控分支中采用SiLU [39]激活函数,即 x ⋅ Sigmoid ( x ) x \cdot \text{Sigmoid}(x) x⋅Sigmoid(x),这可以视为Sigmoid的高级版本。如附录C.1所示,我们发现SiLU既具有Sigmoid的门控效果,又具有稳定的训练属性。我们将 FD ( ⋅ ) \operatorname{FD}(\cdot) FD(⋅)的输出作为输入,将等式(4)重写为:
Z = SiLU ( Conv 1 × 1 ( X ) ) ⏟ F ϕ ⊙ SiLU ( Conv 1 × 1 ( Y C ) ) ⏟ G ψ , Z=\underbrace{\operatorname{SiLU}\left(\operatorname{Conv}_{1 \times 1}(X)\right)}_{\mathcal{F}_{\phi}} \odot \underbrace{\operatorname{SiLU}\left(\operatorname{Conv}_{1 \times 1}\left(Y_{C}\right)\right)}_{\mathcal{G}_{\psi}}, Z=Fϕ SiLU(Conv1×1(X))⊙Gψ SiLU(Conv1×1(YC)),
通过提出的SA块,MogaNet捕获了更多的中阶交互,这在图3b中得到了验证。SA块使用与ConvNeXt中的 D W 7 × 7 DW7 \times 7 DW7×7参数和FLOPS相似的参数和FLOPS,产生了具有辨别力的多阶表示,这超出了现有方法的能力范围,而不需要消耗成本的自注意力。
4.3、通过通道聚合进行多阶特征重新分配
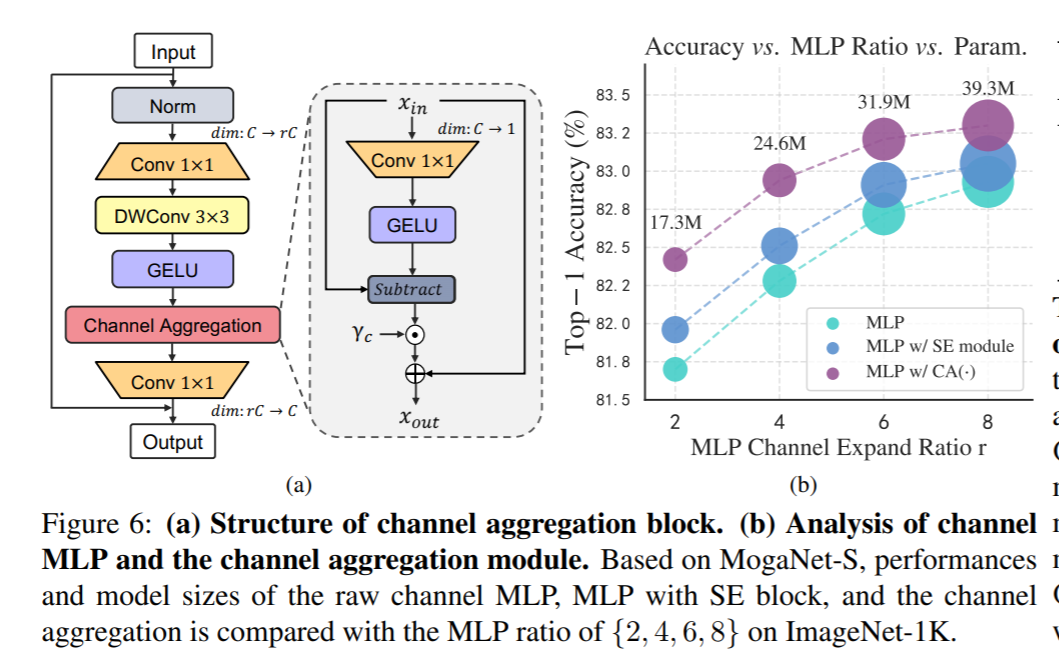
如第2节所述,主流架构主要通过两个线性投影执行通道混合CMixer(.),例如具有通道扩展比率r的2层通道MLP [38, 85, 121]或中间有3×3DWConv的MLP [136, 96, 95]。由于通道间的内在冗余[139,13,119,131],原始MLP需要大量参数(r默认为4或8)才能达到预期的性能,这表明计算效率较低,如图6b所示。为了解决这个问题,当前大多数方法直接将通道增强模块(例如SE模块[60])插入到MLP中。与这些设计不同,我们引入了一个轻量级的通道聚合模块
C
A
(
⋅
)
\mathrm{CA}(\cdot)
CA(⋅)来进行高维隐藏空间中的自适应通道重新分配,并将其进一步扩展为一个通道聚合(CA)块。如图6a所示,我们将等式(3)重写为适用于我们的CA块的等式:
Y
=
GELU
(
DW
3
×
3
(
Conv
1
×
1
(
Norm
(
X
)
)
)
)
,
Z
=
Conv
1
×
1
(
CA
(
Y
)
)
+
X
.
\begin{array}{l} Y=\operatorname{GELU}\left(\operatorname{DW}_{3 \times 3}\left(\operatorname{Conv}_{1 \times 1}(\operatorname{Norm}(X))\right)\right), \\ Z=\operatorname{Conv}_{1 \times 1}(\operatorname{CA}(Y))+X . \end{array}
Y=GELU(DW3×3(Conv1×1(Norm(X)))),Z=Conv1×1(CA(Y))+X.
具体来说,
C
A
(
⋅
)
\mathrm{CA}(\cdot)
CA(⋅)通过一个通道减少投影
W
r
:
R
C
×
H
W
→
R
1
×
H
W
W_{r}: \mathbb{R}^{C \times H W} \rightarrow \mathbb{R}^{1 \times H W}
Wr:RC×HW→R1×HW来实现,并使用GELU来收集和重新分配通道信息:
CA
(
X
)
=
X
+
γ
c
⊙
(
X
−
GELU
(
X
W
r
)
)
,
\operatorname{CA}(X)=X+\gamma_{c} \odot\left(X-\operatorname{GELU}\left(X W_{r}\right)\right),
CA(X)=X+γc⊙(X−GELU(XWr)),
其中, γ c \gamma_{c} γc是初始化为零的通道尺度因子,用于重新分配互补的通道交互 X − GELU ( X W r ) X-\operatorname{GELU}\left(X W_{r}\right) X−GELU(XWr)。如图7所示, C A ( . ) CA (.) CA(.)有效地增强了中阶博弈论交互。图6b验证了 C A ( ⋅ ) \mathrm{CA}(\cdot) CA(⋅)与原始MLP和带有SE模块的MLP在消除通道信息冗余方面的优越性。尽管对基线有一些改进,但带有SE模块的MLP仍然需要大的MLP比率(例如r=6)才能达到预期的性能,同时引入额外的参数和计算开销。相比之下,我们的 C A ( ⋅ ) \mathrm{CA}(\cdot) CA(⋅)使用r=4在较小的额外成本下(0.04M额外参数和0.01G FLOPs)比基线高出0.6%,与使用r=8的基线性能相同。

4.4、实现细节
遵循ConvNets的网络设计风格[86],我们通过在每个阶段堆叠不同数量的空间和通道聚合块,将MogaNet扩展到六种模型大小( X − T i n y X-Tiny X−Tiny、 T i n y Tiny Tiny、 S m a l l Small Small、 B a s e Base Base、 L a r g e Large Large和 X − L a r g e X-Large X−Large),其参数数量与RegNet[103]变体相似。网络配置和超参数详见表A1。FLOPs和吞吐量在附录C.3中进行了分析。我们将多阶DWConv层的通道设置为 C l : C m : C h = 1 : 3 : 4 C_{l}: C_{m}: C_{h}=1: 3: 4 Cl:Cm:Ch=1:3:4(见附录C.2)。类似于[124, 72, 77],MogaNet中的第一个嵌入茎被设计为两个堆叠的 3 × 3 3 \times 3 3×3卷积层,步长为2,而在其他三个阶段中采用单层版本作为嵌入茎。我们选择GELU[54]作为通用激活函数,并且仅在Moga模块中使用SiLU,如等式(8)所示。
5、实验
为了验证MogaNet并与领先的网络架构进行比较,我们在流行的视觉任务上进行了大量实验,包括图像分类、目标检测、实例和语义分割、2D和3D姿态估计以及视频预测。实验使用PyTorch实现,并在NVIDIA A100 GPU上运行。
5.1、ImageNet分类
设置。对于在ImageNet [34]上的分类实验,我们按照标准程序[122, 85]在ImageNet-1K(IN-1K)上训练MogaNet变体,以进行公平比较。我们使用AdamW [89]优化器训练300个周期,基础学习率为1×10^-3,并使用Cosine调度器[88]。为了探索大型模型的容量,我们按照[86]在ImageNet-21K(IN-21K)上对MogaNet-XL进行了90个周期的预训练,然后在IN-1K上进行了30个周期的微调。附录A.2和D.1提供了实现细节和更多结果。我们比较了三种典型的架构:纯ConvNets(C)、Transformers(T)和混合模型(H),后者同时包含自注意力和卷积操作。
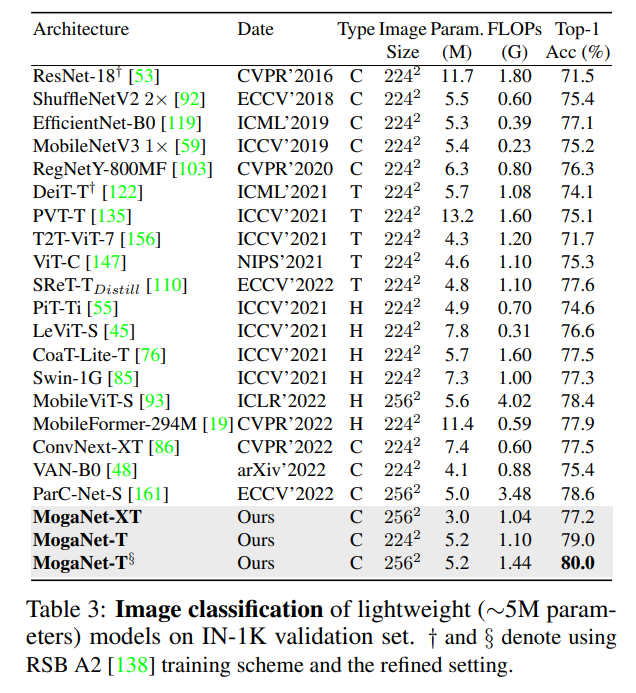
结果。至于轻量级模型,表3显示,MogaNet-XT/T在参数和FLOPs的有效使用方面显著优于现有的轻量级架构。MogaNet-T在
22
4
2
224^2
2242分辨率下实现了79.0%的top-1准确率,这将具有约5M参数的模型提高了至少1.1%。使用
25
6
2
256^2
2562分辨率,MogaNet-T在细化设置下实现80.0%的top-1准确率的同时,比当前的SOTA ParC-Net-S高出1.0%。即使只有3M参数,MogaNet-XT仍然超过了具有大约4M参数的模型,例如比T2T-ViT-7高出4.6%。特别是,
M
o
g
a
N
e
t
−
T
S
MogaNet-T^S
MogaNet−TS使用
25
6
2
256^2
2562分辨率和细化的训练设置(详见附录C.5)实现了80.0%的top-1准确率。至于表4中的放大模型,MogaNet在具有相似参数和计算成本的条件下,显示出优于或可与SOTA架构相媲美的性能。例如,MogaNet-S实现了83.4%的top-1准确率,以2.1和1.2的明显优势超过了Swin-T和ConvNeXt-T。MogaNet-B/L也改进了最近提出的ConvNets,参数更少,例如比HorNet-S/B和SLaK-S/B高出+0.3/0.4和+0.5/0.7个点。当在IN 21K上进行预训练时,MogaNet-XL被提升至87.8%的top-1准确率,参数为181M,与ConvNeXtXL相比节省了169M。值得注意的是,MogaNet-XL可以在没有预训练的情况下在224^2分辨率下达到85.1%,并使ConvNeXtL提高了0.8%,这表明MogaNets比现有模型更容易收敛(这一点也在附录D.1中得到了验证)。
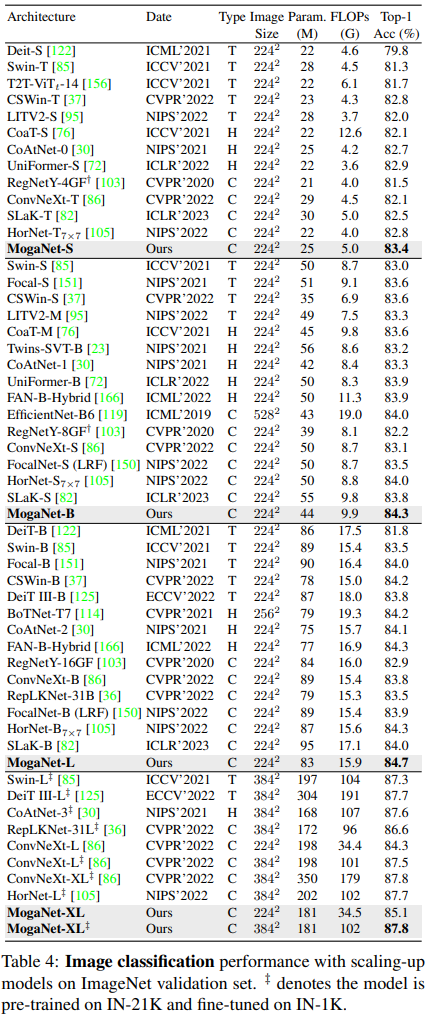
5.2、密集预测任务
COCO上的目标检测和分割。我们在COCO [81]上使用RetinaNet [80]、MaskRCNN [52]和Cascade Mask R-CNN [12]作为检测器,评估了MogaNet在目标检测和实例分割任务上的性能。遵循[85, 86]中的训练和评估设置,我们使用AdamW优化器在COCO train2017上对模型进行1倍和3倍训练计划的微调,并在COCO val2017上进行评估,这是在MMDetection [17]代码库上实现的。采用
b
o
x
m
A
P
(
A
P
b
)
box mAP(AP^b)
boxmAP(APb)和
m
a
s
k
m
A
P
(
A
P
m
)
mask mAP(AP^m)
maskmAP(APm)作为评估指标。有关详细设置和完整结果,请参阅附录A.3和D.2。表5显示,使用MogaNet变体的检测器显著优于之前的骨干网络。值得注意的是,Mask R-CNN与MogaNet-T结合使用实现了
42.6
A
P
b
42.6 AP^b
42.6APb,比Swin-T高出0.4,同时参数和FLOPs分别减少了48%和27%。使用高级训练设置和IN-21K预训练权重,Cascade Mask R-CNN与MogaNet-XL结合使用实现了
56.2
A
P
b
56.2 AP^b
56.2APb,比ConvNeXt-L和RepLKNet-31L分别高出1.4和2.3。
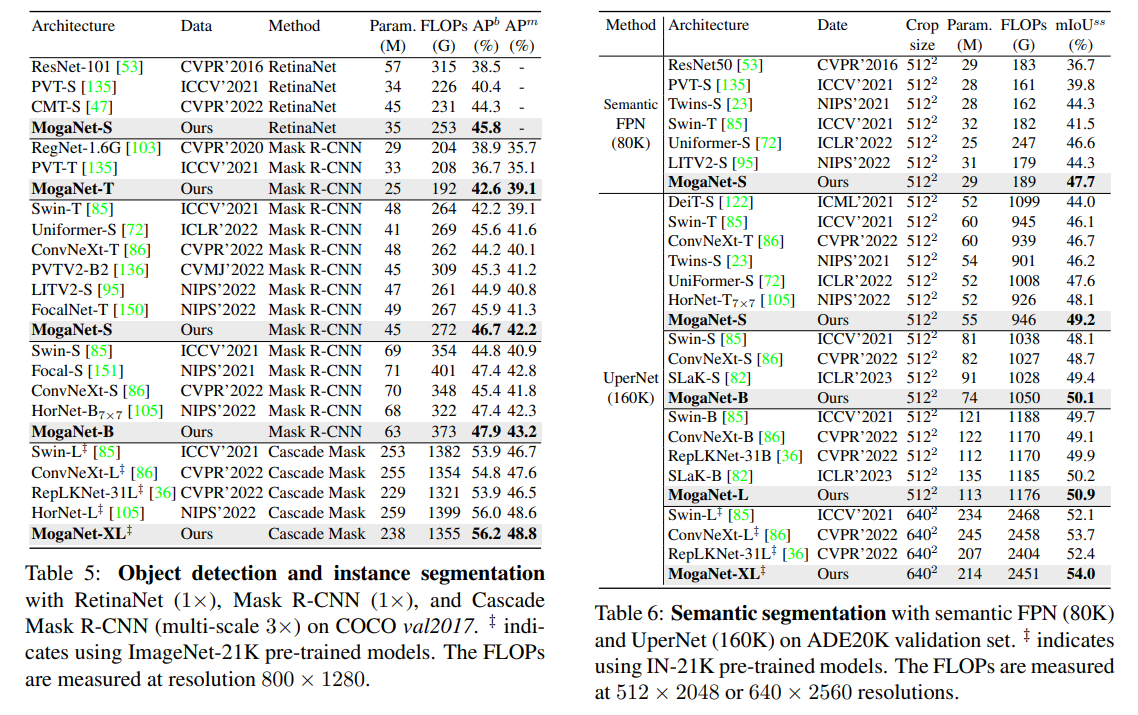
ADE20K上的语义分割。我们还在ADE20K [165]上使用Semantic FPN [69]和UperNet [146]评估了MogaNet在语义分割任务上的性能,遵循[85, 154]的实现,在MMSegmentation [24]代码库上进行。性能通过单尺度mIoU来衡量。使用IN-1K或IN-21K预训练权重进行初始化,Semantic FPN和UperNet通过AdamW优化器进行80K和160K次迭代的微调。有关详细设置和完整结果,请参阅附录A.4和D.3。在表6中,使用MogaNet-S的Semantic FPN始终优于Swin-T和Uniformer-S,分别高出6.2和1.1个点;使用MogaNet-S/B/L的UperNet比ConvNeXt-T/S/B分别提高了 2.5 / 1.4 / 1.8 2.5/1.4/1.8 2.5/1.4/1.8个点。使用更高的分辨率和IN-21K预训练,MogaNet-XL实现了54.0 SS mIoU,超过ConvNeXt-L和RepLKNet-31L分别0.3和1.6个点。
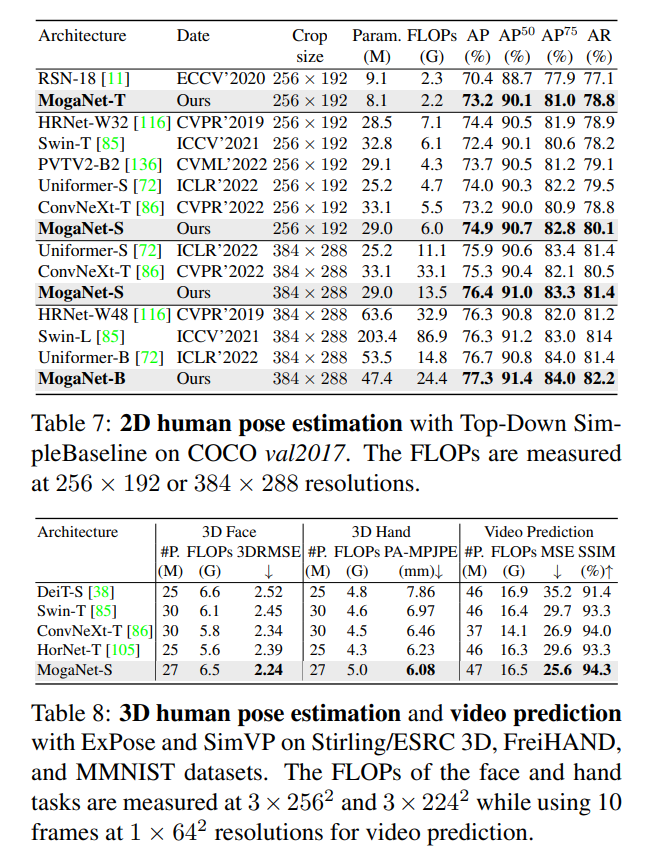
2D和3D人体姿态估计。接着,我们评估了MogaNet在2D和3D人体姿态估计任务上的性能。对于COCO上的2D关键点估计,我们按照[135, 72]的方法使用SimpleBaseline[145]进行评估,该方法通过Adam优化器对模型进行210个epoch的微调。表7显示,对于256×192的输入,MogaNet变体至少提高了0.9的AP,例如,MogaNet-S相对于Swin-T和PVTV2-B2分别提高了2.5和1.2。使用384×288的输入,MogaNet-B在参数更少的情况下,性能比Swin-L和Uniformer-B分别高出1.0和0.6的AP。对于Stirling/ESRC 3D[41]和FreiHAND[169]数据集上的3D面部/手部表面重建任务,我们使用ExPose[22]对骨干网络进行基准测试,该方法通过Adam优化器对模型进行100个epoch的微调。3DRMSE和平均每关节位置误差(PA-MPJPE)是评估指标。在表8中,与Transformer和ConvNet相比,MogaNet-S显示出最低的误差。我们在附录D.4和D.5中提供了2D和3D姿态估计任务的详细实现和结果。
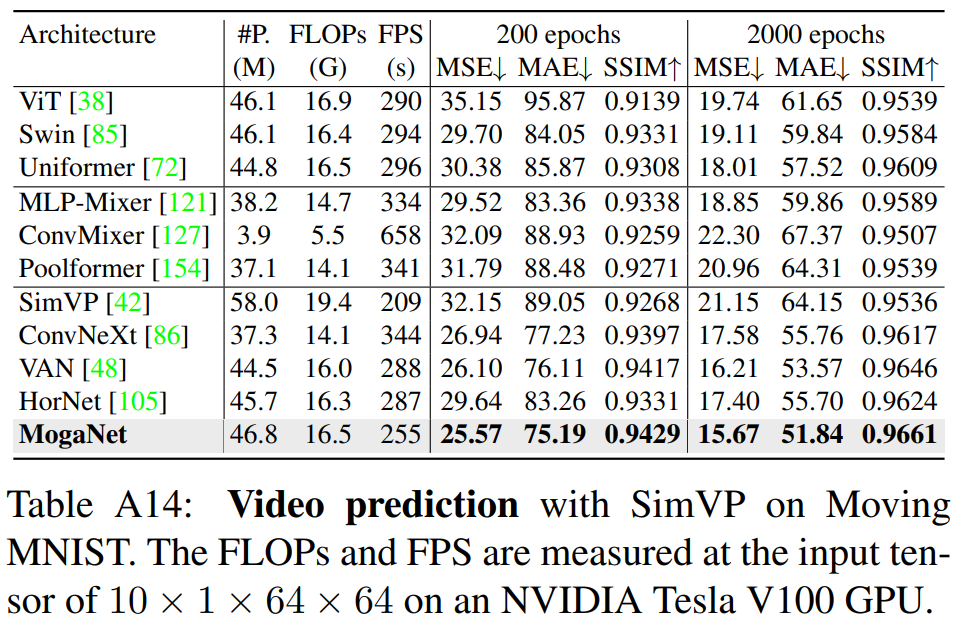
视频预测。我们进一步使用SimVP[42]在MMNIST[115]上评估了MogaNet在无监督视频预测任务上的性能,其中模型以给定的10帧作为输入,预测接下来的10帧。我们使用Adam优化器从头开始训练模型200个epoch,并通过MSE和结构相似性指数(SSIM)进行评估。表8显示,使用MogaNet块的SimVP相对于基线提高了6.58的MSE,并且性能优于ConvNeXt和HorNet,分别提高了1.37和4.07的MSE。附录A.7和D.6显示了更多的实验设置和结果。

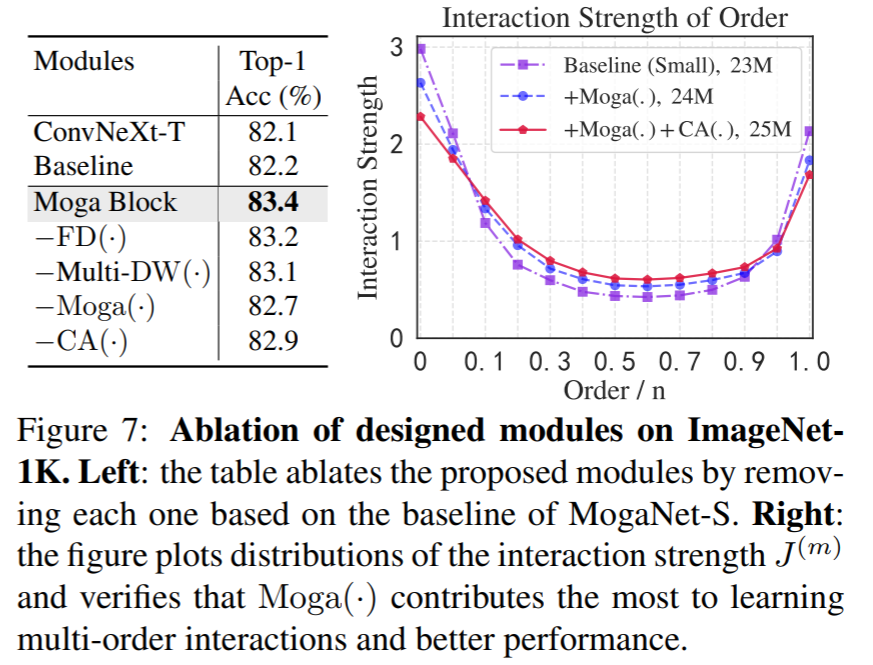
5.3、消融实验和分析
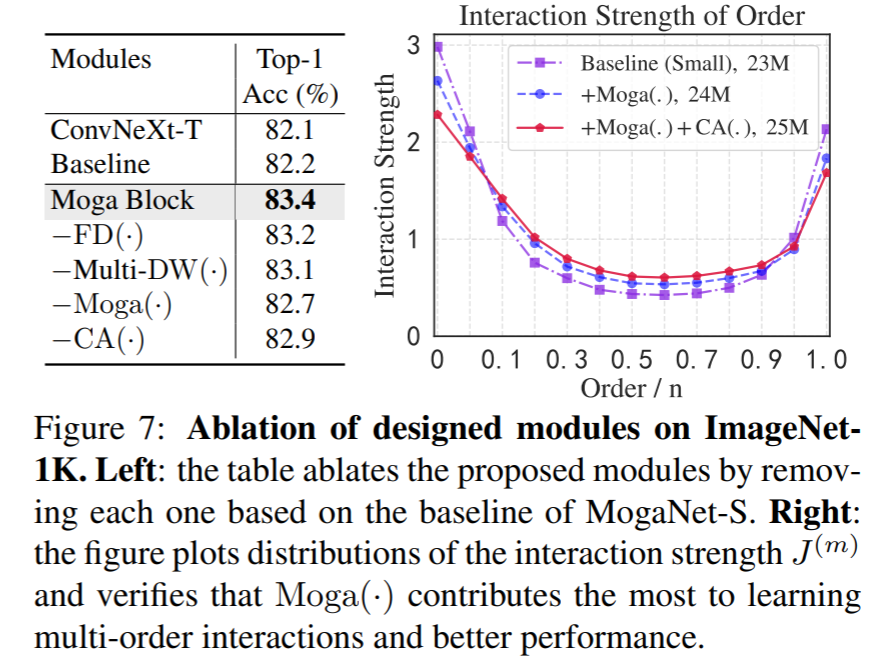
我们首先在表2和图7(左)中消除了空间聚合模块,包括 F D ( ⋅ ) FD(\cdot) FD(⋅)和 M o g a ( ⋅ ) Moga(\cdot) Moga(⋅),其中包含门控分支和具有多阶DWConv层 M u l t i − D W ( ⋅ ) Multi-DW(\cdot) Multi−DW(⋅)的上下文分支,以及通道聚合模块 C A ( ⋅ ) \mathbf{C A}(\cdot) CA(⋅)。我们发现所有提出的模块都能在付出一些代价的情况下带来改进。附录C提供了更多的消融实验。此外,我们在图7(右)中通过与现有模型进行比较,通过Grad-CAM[108]可视化类激活映射(CAM),经验性地展示了设计模块可以学习到更多的中阶交互。
6、结论
在本文中,我们提出了MogaNet,这是一种从多阶博弈论交互的新颖视角出发的计算高效的纯ConvNet架构。通过特别关注多阶博弈论交互,我们设计了一个统一的Moga块,它能够有效地在空间和通道空间中捕获鲁棒的多阶上下文。大量的实验验证了MogaNet在各种视觉基准测试上与代表性的ConvNets、ViTs和混合架构相比,在准确性和计算效率方面的一致优势。
致谢
本工作得到了国家重点研发计划(编号:2022ZD0115100)、国家自然科学基金项目(编号:U21A20427)以及西湖大学生合生物与生物工程中心项目(编号:WU2022A009)的资助。本文是在西湖大学实习期间完成的,由Zedong Wang和Zhiyuan Chen在西湖大学实习期间完成。我们感谢西湖大学AI站提供的GPU支持。感谢Mengzhao Chen、Zhangyang Gao、Jianzhu Guo、Fang Wu和匿名审稿人对本文的润色。
A、实现细节
A.1、架构细节
MogaNet的详细架构规格如表A1和图A1所示,其中假设所有架构的输入图像分辨率为
22
4
2
224^2
2242。我们重新调整了不同规模的模型对应于每个阶段的组嵌入维度数和Moga块的数目:i) MogaNetX-Tiny和MogaNet-Tiny的嵌入维度数为{32,64,96,192}和{32,64,128,256},具有竞争力的参数数量和计算负载,与最近提出的轻量级架构相媲美[93, 19, 161];ii) MogaNet-Small采用的嵌入维度数为{64,128,320,512},与其他流行的小规模架构进行比较[85, 86];iii) MogaNet-Base的嵌入维度数为{64,160,320,512},与其他中等规模的架构进行比较;iv) MogaNet-Large的嵌入维度数为{64,160,320,640},专为大规模计算机视觉任务而设计。v) MogaNet-XLarge的嵌入维度数为{96,192,480,960},是专为大规模任务而设计的扩展版本(约200M个参数)。在ImageNet分辨率
22
4
2
224^2
2242上进行图像分类时测量FLOPs,其中在最后一个阶段的输出特征图上应用全局平均池化(GAP)层,然后是一个线性分类器。
A.2、ImageNet实验设置
我们在ImageNet [34]数据集上进行图像分类实验。所有实验都在OpenMixup [74]和timm [138]代码库上在8个NVIDIA A100 GPU上实现。更多结果请参阅附录D.1。
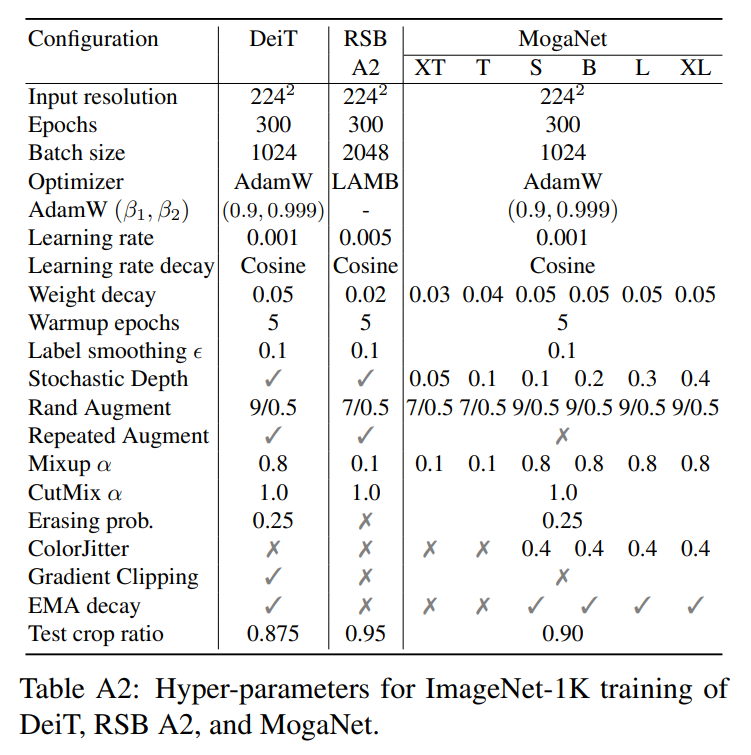
ImageNet-1K。我们按照DeiT [122]和RSB A2 [138]的训练设置进行常规的ImageNet-1K训练,这些设置在Transformer和ConvNet架构中得到广泛应用。对于所有模型,从头开始训练的默认输入图像分辨率为224^2。对于轻量级实验,我们根据MobileViT [93]采用
25
6
2
256^2
2562分辨率。以模型参数超过25M或更多的训练设置为准,我们使用AdamW [89]优化器、批量大小为1024、基本学习率为1×10−3、权重衰减为0.05以及5个线性预热周期的余弦学习率调度器[88]训练所有MogaNet模型300个周期。至于数据增强和正则化技术,我们采用DeiT训练设置中的大多数数据增强和正则化策略,包括随机缩放裁剪(RRC)和水平翻转[117],RandAugment [28],Mixup [160],CutMix [158],随机擦除[164],ColorJitter [53],随机深度[62]和标签平滑[118]。与ConvNeXt [86]类似,我们不应用专为Transformer设计的重复增强[57]和梯度裁剪,因为这些技术不能提高ConvNets的性能,同时默认使用衰减率为0.9999的指数移动平均(EMA) [101]。我们还删除了其他增强策略[27,84,73,83],例如PCA照明[70]和AutoAugment [27]。由于轻量级架构(3.1亿参数)在经过强烈的增强和正则化后往往会出现欠拟合,我们根据[93, 19, 161]调整了MogaNet-XT/T的训练配置,包括使用权重衰减0.03和0.04,Mixup的
α
\alpha
α值为0.1,以及MogaNet-XT/T的RandAugment为7/0.5。由于EMA被提出用于稳定大模型的训练过程,因此为了公平比较,我们也将其从MogaNet-XT/T中移除。对于较大的模型,我们采用增加程度的随机深度路径增强。在评估中,使用单个剪裁,测试剪裁比例为0.9时报告的top-1准确度为[156,154,48]。
ImageNet-21K。根据ConvNeXt [86],我们进一步提供了ImageNet-21K [34]预训练和ImageNet-1K高分辨率微调的训练方案,具体如表A3所示。预训练阶段移除了EMA,微调阶段移除了CutMix和Mixup。
A.3、COCO上的目标检测和实例分割
根据Swin [85]和PoolFormer [154]的研究,我们在COCO [81]基准上评估目标检测和实例分割任务,该基准包括118K训练图像(train2017)和5K验证图像(val2017)。我们采用Mask-RCNN [52]作为标准检测器,并使用ImageNet-1K预训练权重作为骨干网络的初始化。我们使用AdamW [89]优化器进行1×调度器(12个周期)的训练,基本学习率为 1 × 1 0 − 4 1 \times 10^{-4} 1×10−4,批量大小为16。根据需要使用ImageNet-1K和ImageNet-21K上的预训练权重来初始化骨干网络。训练图像的短边调整为800像素,长边调整为不超过1333像素。我们在800×1280分辨率下计算比较模型的FLOPs。COCO检测实验在MMDetection [17]代码库上实现,并在8个NVIDIA A100 GPU上运行。详细结果请参阅附录D.2。
A.4、ADE20K上的语义分割
我们在ADE20K [165]基准上评估语义分割,该基准包含20K训练图像和2K验证图像,涵盖150个细粒度语义类别。我们首先采用Semantic FPN [69],遵循PoolFormer [154]和Uniformer [72]的方法,使用AdamW [89]优化器训练模型80K次迭代,基本学习率为 2 × 1 0 − 4 2 \times 10^{-4} 2×10−4,批量大小为16,并使用多项式学习率调度器。然后,我们利用UperNet [146]遵循Swin [85]的方法,该方法使用AdamW优化器,基本学习率为 6 × 1 0 − 5 6 \times 10^{-5} 6×10−5,权重衰减为0.01,多项式调度器具有1500次迭代的线性预热。我们相应地使用ImageNet-1K和ImageNet-21K预训练权重来初始化骨干网络。训练图像被调整为 51 2 2 512^2 5122分辨率,测试图像的短边被调整为512像素。我们在800×2048分辨率下计算模型的FLOPs。ADE20K分割实验在MMSegmentation [24]代码库上实现,并在8个NVIDIA A100 GPU上运行。完整的比较结果请参阅附录D.3。
A.5、COCO上的2D人体姿态估计
我们在COCO [81]基准上评估2D人体关键点估计任务,基于Top-Down SimpleBaseline [145](在骨干网络后添加一个Top-Down估计头),遵循PVT [135]和UniFormer [72]的方法。我们使用Adam优化器[68]对所有模型进行210个周期的微调,基本学习率选择在 { 1 × 1 0 − 3 , 5 × 1 0 − 4 } \left\{1 \times 10^{-3}, 5 \times\right. \left.10^{-4}\right\} {1×10−3,5×10−4}中,多步学习率调度器在170和200个周期时衰减。使用ImageNet-1K预训练权重作为骨干网络的初始化。训练和测试图像被调整为256×192或384×288分辨率,并在这两种分辨率下计算模型的FLOPs。COCO姿态估计实验在MMPose [25]代码库上实现,并在8个NVIDIA A100 GPU上运行。完整的实验结果请参阅附录D.4。
A.6、3D人体姿态估计
我们使用单目图像对MogaNet和流行的架构进行3D人体姿态估计任务评估,基于ExPose [22]。首先,我们使用ExPose对广泛使用的ConvNet进行3D人脸网格表面估计任务的基准测试。所有模型在Flickr-Faces-HQ Dataset (FFHQ) [67]上进行100个周期的训练,并在Stirling/ESRC 3D dataset [41]上进行测试,该数据集包含带有地面实况3D面部扫描的面部RGB图像。3D Root Mean Square Error (3DRMSE)衡量预测和地面实况面部扫描之间的误差。根据ExPose,使用Adam优化器,批量大小为256,基本学习率选择在 { 2 × 1 0 − 4 , 1 × 1 0 − 4 } \left\{2 \times 10^{-4}, 1 \times 10^{-4}\right\} {2×10−4,1×10−4}中,多步学习率调度器在60和100个周期时衰减。ImageNet-1K预训练权重被用作骨干网络的初始化。训练和测试图像被调整为256×256分辨率。然后,我们评估用于手部3D姿态估计任务的ConvNets。FreiHAND dataset [169],包含多视图RGB手部图像、3D MANO手部姿态和形状注释,用于训练和测试。Mean Per-Joint Position Error (PAMPJPE)用于评估3D骨架。请注意,“PA”前缀表示该指标在通过Procrustes对齐解决旋转、缩放和平移变换后测量误差。有关更多实现细节,请参阅ExPose。所有模型使用与3D人脸任务相同的训练设置,训练和测试分辨率为224×224。3D姿态估计实验在MMHuman3D [26]代码库上实现,并在4个NVIDIA A100 GPU上运行。完整的结果请参阅附录D.5。
A.7、移动MNIST上的视频预测
我们使用SimVP [42]对各种Metaformer架构[154]和MogaNet进行视频预测任务的评估,基于Moving MNIST (MMNIST) [81]。请注意,SimVP的隐藏翻译器是一个2D网络模块,用于学习时空表示,任何2D架构都可以替换。因此,我们可以在SimVP框架的基础上对各种架构进行基准测试。在MMNIST [115]中,每个视频随机生成20帧,包含两个64×64分辨率的数字,模型使用10帧作为输入来预测下一个10帧。视频预测通过均方误差(MSE)、平均绝对误差(MAE)和结构相似性指数(SSIM)进行评估。所有模型从头开始在MMNIST上训练200或2000个周期,使用Adam优化器、批量大小为16、OneCycle学习率调度器、初始学习率选择在 { 1 × 1 0 − 2 , 5 × 1 0 − 3 , 1 × 1 0 − 3 , 5 × 1 0 − 4 } \left\{1 \times 10^{-2}, 5 \times 10^{-3}, 1 \times\right. \left.10^{-3}, 5 \times 10^{-4}\right\} {1×10−2,5×10−3,1×10−3,5×10−4}中。视频预测实验在SimVPv2代码库上实现,并在单个NVIDIA Tesla V100 GPU上运行。完整的基准测试结果请参阅附录D.6。
B、实验结果
B.1、DNNs的表示瓶颈:多阶交互视角
多阶博弈论交互。在3部分,我们通过多阶博弈论交互的视角解释了DNNs学到的表示[162, 33],这可以将DNN中变量之间的通信效果分解为不同交互阶数的不同博弈论组件。这里的阶数指的是博弈论交互的计算过程中涉及的上下文规模。
对于计算机视觉,第m阶交互 I ( m ) ( i , j ) I^{(m)}(i, j) I(m)(i,j)衡量图像补丁i和j在所有m个图像补丁上下文中的平均博弈论交互效果。以面部识别为例,我们可以将补丁i和j视为面部的两只眼睛。此外,我们还考虑了脸部上包含的其他m个可见图像补丁。眼睛补丁i和j对任务的的作用和贡献取决于这些m个可见补丁作为上下文,这通过上述 I ( m ) ( i , j ) I^{(m)}(i, j) I(m)(i,j)来衡量。如果 I ( m ) ( i , j ) > 0 I^{(m)}(i, j)>0 I(m)(i,j)>0,则在m个上下文中,补丁i和j显示出正效应。相应地,如果 I ( m ) ( i , j ) < 0 I^{(m)}(i, j)<0 I(m)(i,j)<0,我们考虑在m个上下文中,i和j具有负效应。更重要的是,低阶交互主要反映广泛共享的局部纹理和常见的视觉概念。中等阶交互主要负责编码判别性的高层次表示。然而,高阶交互倾向于让DNNs记忆稀有异常值的模式和大规模形状,这些模式具有密集的全球交互,这可能会导致我们的深度模型过度拟合[33,20]。因此,在深度架构中发生过度低阶或高阶博弈论交互可能是不希望的。
正式来说,给定一个输入图像 x 以及一组 n 个补丁
N
=
{
1
,
…
,
n
}
N=\{1, \ldots, n\}
N={1,…,n}(例如,一个总共有 n 个像素的图像),多阶交互
I
(
m
)
(
i
,
j
)
I^{(m)}(i, j)
I(m)(i,j) 可以计算为:
I
(
m
)
(
i
,
j
)
=
E
S
⊆
N
\
{
i
,
j
}
,
∣
S
∣
=
m
[
Δ
f
(
i
,
j
,
S
)
]
,
I^{(m)}(i, j)=\mathbb{E}_{S \subseteq N \backslash\{i, j\},|S|=m}[\Delta f(i, j, S)],
I(m)(i,j)=ES⊆N\{i,j},∣S∣=m[Δf(i,j,S)],
其中
Δ
f
(
i
,
j
,
S
)
=
f
(
S
∪
{
i
,
j
}
)
−
f
(
S
∪
{
i
}
)
−
f
(
S
∪
{
j
}
)
+
f
(
S
)
\Delta f(i, j, S)=f(S \cup\{i, j\})-f(S \cup\{i\})-f(S \cup \{j\})+f(S)
Δf(i,j,S)=f(S∪{i,j})−f(S∪{i})−f(S∪{j})+f(S)。
f
(
S
)
\quad f(S)
f(S) 表示在
N
\
S
N \backslash S
N\S 中的补丁保持不变,但替换为基线值时的输出分数 [2]。例如,低阶交互(例如,
m
=
0.05
n
m=0.05 n
m=0.05n)意味着在较小的上下文范围内变量
i
,
j
i, j
i,j 之间的相对简单的协作,而高阶交互(例如,
m
=
0.95
n
m=0.95 n
m=0.95n)对应于在较大的上下文范围内的复杂协作。然后,我们可以通过编码的 m-阶交互的相对交互强度
J
(
m
)
J^{(m)}
J(m) 来衡量深度神经网络(DNNs)的整体交互复杂性:
J
(
m
)
=
E
x
∈
Ω
E
i
,
j
∣
I
(
m
)
(
i
,
j
∣
x
)
∣
E
m
′
E
x
∈
Ω
E
i
,
j
∣
I
(
m
′
)
(
i
,
j
∣
x
)
∣
,
J^{(m)}=\frac{\mathbb{E}_{x \in \Omega} \mathbb{E}_{i, j}\left|I^{(m)}(i, j \mid x)\right|}{\mathbb{E}_{m^{\prime}} \mathbb{E}_{x \in \Omega} \mathbb{E}_{i, j}\left|I^{\left(m^{\prime}\right)}(i, j \mid x)\right|},
J(m)=Em′Ex∈ΩEi,j
I(m′)(i,j∣x)
Ex∈ΩEi,j
I(m)(i,j∣x)
,
其中, Ω \Omega Ω 是所有样本的集合, 0 ≤ m ≥ n − 2 0 \leq m \geq n-2 0≤m≥n−2。请注意, J ( m ) J^{(m)} J(m) 是输入样本中所有可能补丁对上的平均交互强度,它表示深度神经网络(DNNs)交互作用的分布(曲线下面积总和为1)。在图3中,我们使用官方实现提供的[33]中的模型,在ImageNet-1K上训练的模型上,使用公式12计算了交互强度 J ( m ) J^{(m)} J(m)。特别地,我们使用 224 × 224 224 \times 224 224×224分辨率的图像作为输入,并在 14 × 14 14 \times 14 14×14 的网格上计算 J ( m ) J^{(m)} J(m),即 n = 14 × 14 n=14 \times 14 n=14×14。对于掩码样本 x S x_{S} xS,我们将模型输出设为 f ( x S ) = log P ( y ^ = y ∣ x S ) 1 − P ( y ^ = y ∣ x S ) f\left(x_{S}\right)=\log \frac{P\left(\hat{y}=y \mid x_{S}\right)}{1-P\left(\hat{y}=y \mid x_{S}\right)} f(xS)=log1−P(y^=y∣xS)P(y^=y∣xS),其中 (y) 表示真实标签, P ( y ^ = y ∣ x S ) P\left(\hat{y}=y \mid x_{S}\right) P(y^=y∣xS) 表示将掩码样本 x S x_{S} xS分类到真实类别的概率。
自视觉转换器(ViTs)在广泛的计算机视觉任务中兴起以来,最近的研究主要从两个方向探讨为什么ViTs有效:(a)对噪声的鲁棒性评估发现,ViTs中的自注意力[94, 97, 167, 75]或门控机制[166]比经典的卷积操作[113,118]更鲁棒。例如,即使目标对象有大的遮挡比例(例如,只有10%~20%的可见补丁)或受到损坏噪声的影响,ViTs仍然可以识别目标对象。这种现象可能源于图像的固有冗余性和自注意力机制的竞争性质[134,140]。最近的一些工作[152, 45]表明,ViTs可以通过动态采样策略使用一些关键令牌(例如,根据输入图像的复杂性选择的50%)来工作,这也利用了自注意力的特征选择性质。从多阶交互的角度来看,具有局部归纳偏置的卷积(使用小核大小)倾向于低阶交互,而没有任何归纳偏置的自注意力倾向于学习低阶和高阶交互。(b)对分布外样本的评估表明,自注意力机制和具有大核设计的深度卷积(DWConv)与人类视觉具有相似的形状偏置倾向[128, 43, 36],而规范的ConvNets(使用小核大小的卷积)对局部纹理有强烈的偏置[44, 56]。当前的工作[36]将形状或纹理偏置倾向归因于自注意力或卷积操作的感受野,即具有较大感受野或更多长程依赖的操作更可能是形状偏置。然而,形状偏置操作与人类视觉之间仍然存在差距。人类大脑[126,33]获取视觉模式和线索,并进行中等复杂度的交互来识别物体,而自注意力或卷积操作只能编码全局或局部特征来进行高或低复杂度的交互。由于现有的深度神经网络(DNNs)设计只是以级联的方式堆叠区域感知或上下文聚合操作,因此不可避免地会遇到表示瓶颈。
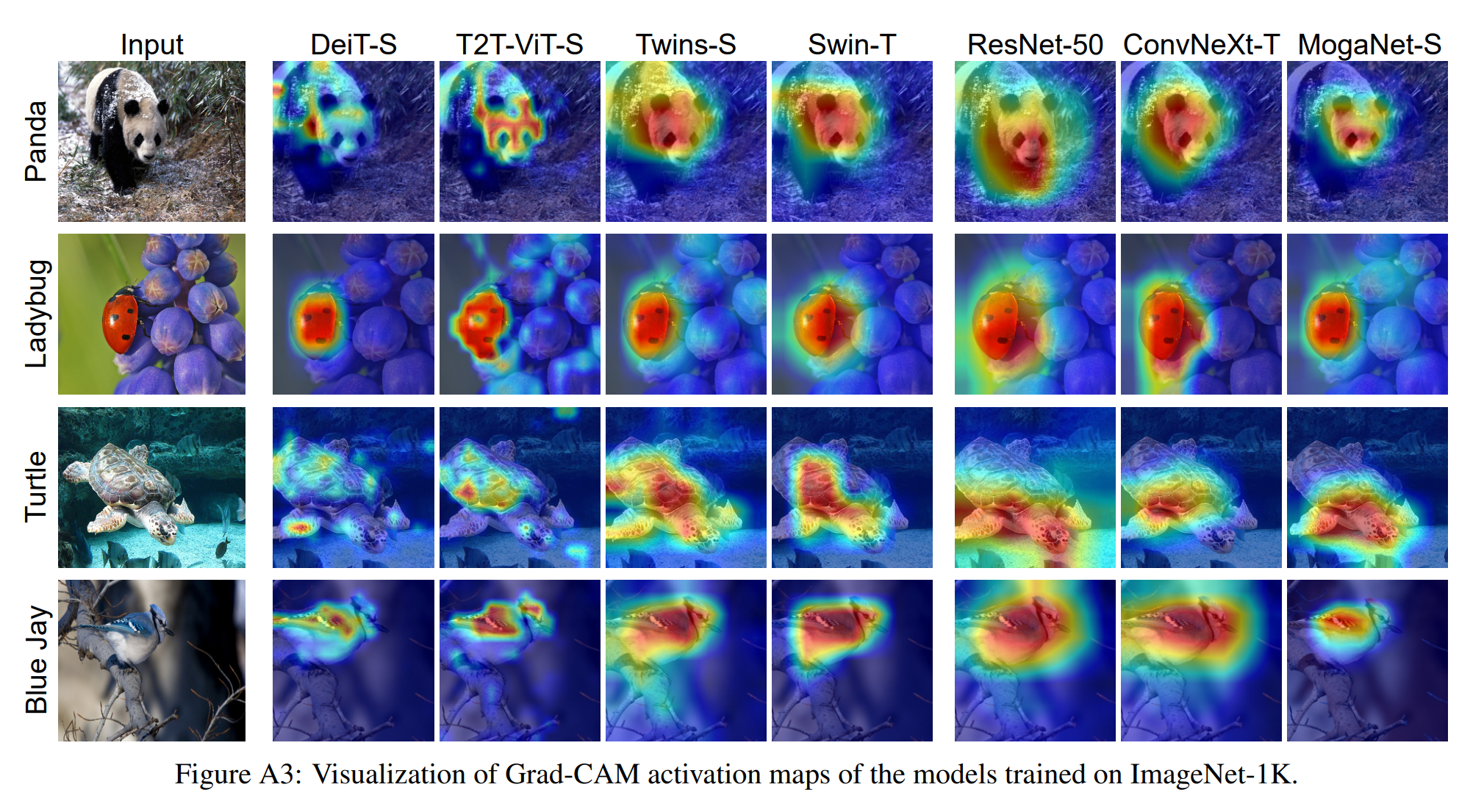
我们在图A3中进一步可视化了与Transformer(包括DeiT-S [122]、T2T-ViT-S [156]、TwinsS [23]和Swin [85])和ConvNets(包括ResNet50 [53]和ConvNeXt-T [86])相比,MogaNet-S的更多Grad-CAM [108]激活图示例。由于自注意力机制,纯Transformer架构(DeiT-S和T2T-ViT-S)显示出比ConvNets更精细的激活图,但它们也激活了一些不相关的部分。结合局部窗口的设计,局部注意力架构(Twins-S和Swin-T)可以定位完整的语义对象。以前的ConvNets的结果可以大致定位语义目标,但可能包含一些背景区域。我们提出的MogaNet-S的激活部分与以前的ConvNets相比,更类似于局部注意力架构,它们更多地聚集在语义对象上。
C、更多消融和分析结果
除了第5.3节之外,我们在ImageNet-1K上进一步对我们提出的MogaNet进行了更多的消融和分析。我们采用了与第2节相同的实验设置。
C.1、激活函数的消融
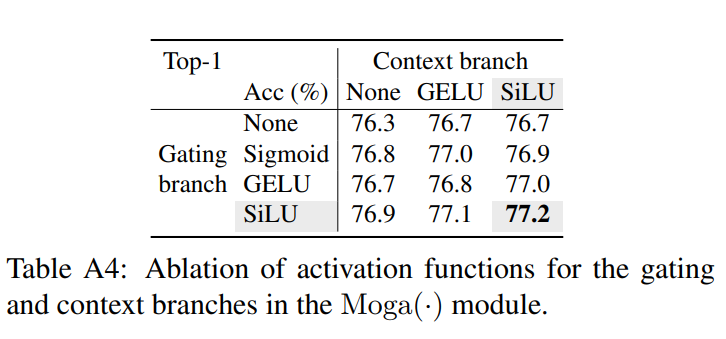
我们在ImageNet-1K上对提出的多阶门控聚合模块中使用的激活函数进行了消融实验。表A4显示,在两个分支上都使用SiLU [39]激活函数可以获得最佳性能。在Transformer中也发现了类似的结果,例如,使用SiLU或GELU [54]的GLU变体比使用Sigmoid或Tanh激活函数 [109, 61]的性能更好。我们假设SiLU是最适合的激活函数,因为它同时拥有Sigmoid(门控效应)和GELU(训练友好)的特性,其定义为 x ⋅ Sigmoid ( x ) x \cdot \operatorname{Sigmoid}(x) x⋅Sigmoid(x) 。
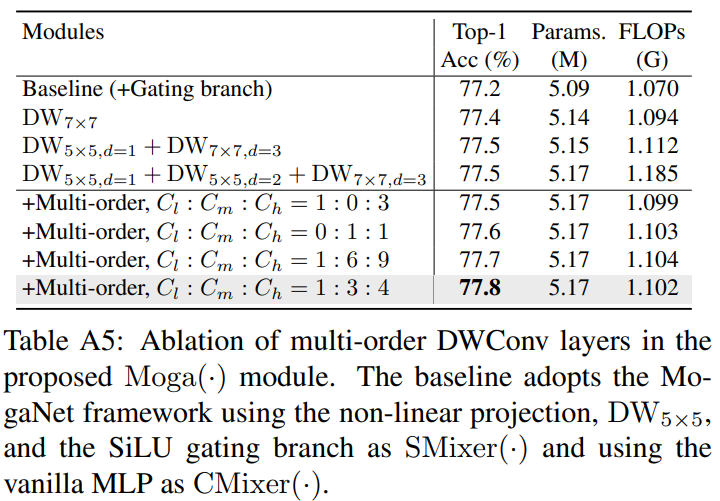
C.2、多阶DWConv层的消融
除了第4.2节和第5.3节之外,我们还在ImageNet-1K上分析了多阶聚合模块 Moga ( ⋅ ) \operatorname{Moga}(\cdot) Moga(⋅) 中的多阶深度可分离卷积(DWConv)层作为静态区域感知。如表A5所示,我们分析了三个并行扩张DWConv层的通道配置: D W 5 × 5 , d = 1 , D W 5 × 5 , d = 2 \mathrm{DW}_{5 \times 5, d=1}, \mathrm{DW}_{5 \times 5, d=2} DW5×5,d=1,DW5×5,d=2和 D W 7 × 7 , d = 3 \mathrm{DW}_{7 \times 7, d=3} DW7×7,d=3,其通道数为 C l , C m , C h C_{l}, C_{m}, C_{h} Cl,Cm,Ch。我们首先比较了串行DWConv层(例如, D W 5 × 5 , d = 1 + D W 7 × 7 , d = 3 \mathrm{DW}_{5 \times 5, d=1}+\mathrm{DW}_{7 \times 7, d=3} DW5×5,d=1+DW7×7,d=3)和并行DWConv层的性能。我们发现并行设计可以在更少的计算负载下实现相同的性能,因为DWConv内核被平等地应用于所有通道。当我们采用三个DWConv层时,与这些DWConv层的串行堆叠相比,我们提出的并行设计减少了 C l + C h C_{l}+C_{h} Cl+Ch和 C l + C m C_{l}+C_{m} Cl+Cm倍的 D W 5 × 5 , d = 2 \mathrm{DW}_{5 \times 5, d=2} DW5×5,d=2和 D W 5 × 5 , d = 2 \mathrm{DW}_{5 \times 5, d=2} DW5×5,d=2的计算量。然后,我们通过经验探索了三个通道的最佳配置。我们发现 C l : C m : C h = 1 : 3 : 4 C_{l}: C_{m}: C_{h}=1: 3: 4 Cl:Cm:Ch=1:3:4产生了最佳性能,这很好地平衡了小、中、大DWConv内核,以学习低、中、高阶上下文表示。我们在下一小节中计算和讨论了所提出的三个DWConv层的FLOPs,以验证其效率。在相关设计[95, 111, 105]中也发现了类似的结论,其中全局上下文聚合占据了大部分(例如, 1 2 ∼ 3 4 \frac{1}{2} \sim \frac{3}{4} 21∼43通道或上下文组件)。我们还基于MogaNet-S/B验证了具有最佳配置的并行设计。因此,我们可以得出结论,我们提出的多阶DWConv层可以有效地学习多阶上下文信息,用于 Moga ( ⋅ ) \operatorname{Moga}(\cdot) Moga(⋅)的上下文分支。
C.3、MogaNet 的 FLOPs 和吞吐量
多阶门控聚合模块的 FLOPs。我们将所提出的多阶门控聚合模块的计算分为两部分:卷积操作,并为每部分计算 FLOPs。
- C o n v 1 × 1 Conv1 \times 1 Conv1×1。 1 × 1 1 \times 1 1×1 卷积操作 ϕ gate \phi_{\text {gate}} ϕgate、 ϕ context \phi_{\text {context}} ϕcontext 和 ϕ out \phi_{\text {out}} ϕout 的 FLOPs 可以推导为:
FLOPs ( ϕ gate ) = 2 H W C 2 , FLOPs ( ϕ context ) = 2 H W C 2 , FLOPs ( ϕ out ) = 2 H W C 2 . \begin{aligned} \operatorname{FLOPs}\left(\phi_{\text {gate }}\right) & =2 H W C^{2}, \\ \operatorname{FLOPs}\left(\phi_{\text {context }}\right) & =2 H W C^{2}, \\ \operatorname{FLOPs}\left(\phi_{\text {out }}\right) & =2 H W C^{2} . \end{aligned} FLOPs(ϕgate )FLOPs(ϕcontext )FLOPs(ϕout )=2HWC2,=2HWC2,=2HWC2.
- 深度卷积:我们考虑具有扩张比率d的深度卷积(DW)。DWConv是对输入X执行的,其中
X
∈
R
H
W
×
C
i
n
X \in \mathbb{R}^{H W \times C_{i n}}
X∈RHW×Cin。因此,Moga模块中所有DW的FLOPs(浮点运算次数)为:
FLOPs ( D W 5 × 5 , d = 1 ) = 2 H W C i n K 5 × 5 2 , FLOPs ( D W 5 × 5 , d = 2 ) = 3 4 H W C i n K 5 × 5 2 , FLOPs ( D W 7 × 7 , d = 3 ) = H W C i n K 7 × 7 2 . \begin{array}{l} \operatorname{FLOPs}\left(\mathrm{DW}_{5 \times 5, d=1}\right)=2 H W C_{i n} K_{5 \times 5}^{2}, \\ \operatorname{FLOPs}\left(\mathrm{DW}_{5 \times 5, d=2}\right)=\frac{3}{4} H W C_{i n} K_{5 \times 5}^{2}, \\ \operatorname{FLOPs}\left(\mathrm{DW}_{7 \times 7, d=3}\right)=H W C_{i n} K_{7 \times 7}^{2} . \end{array} FLOPs(DW5×5,d=1)=2HWCinK5×52,FLOPs(DW5×5,d=2)=43HWCinK5×52,FLOPs(DW7×7,d=3)=HWCinK7×72.
总的来说,我们Moga模块的总FLOPs可以通过以下方式推导:
FLOPs
(
M
o
g
a
)
=
2
H
W
C
i
n
[
11
8
K
5
×
5
2
+
1
2
K
7
×
7
2
+
3
C
i
n
]
=
H
W
C
i
n
[
471
4
+
6
C
i
n
]
.
\begin{aligned} \operatorname{FLOPs}(\mathrm{Moga}) & =2 H W C_{i n}\left[\frac{11}{8} K_{5 \times 5}^{2}+\frac{1}{2} K_{7 \times 7}^{2}+3 C_{i n}\right] \\ & =H W C_{i n}\left[\frac{471}{4}+6 C_{i n}\right] . \end{aligned}
FLOPs(Moga)=2HWCin[811K5×52+21K7×72+3Cin]=HWCin[4471+6Cin].
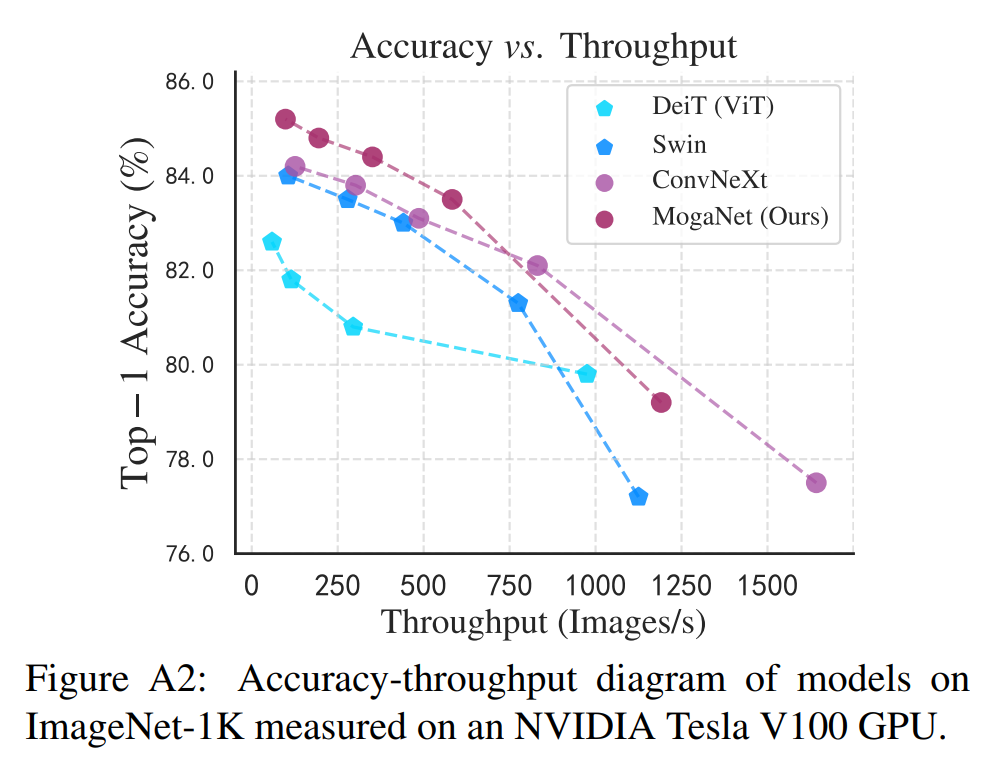
MogaNet的吞吐量。我们进一步在ImageNet-1K数据集上分析了MogaNet变体的吞吐量。如图A2所示,MogaNet的吞吐量与Swin Transformer相似,但性能优于Swin和ConvNet。由于我们在MogaNet中添加了通道分割和全局平均池化(GAP)操作,因此ConvNeXt的吞吐量在某种程度上超过了MogaNet。
C.4、归一化层的消融研究
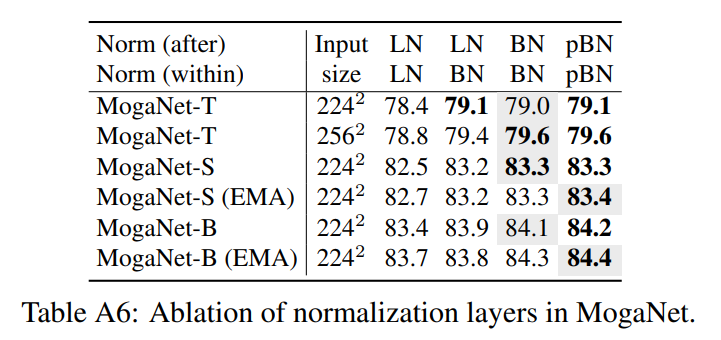
对于大多数ConvNets来说,BatchNorm(BN)[64]被认为是提高收敛速度和防止过拟合的重要组件。然而,BN可能会引起一些不稳定性[144]或损害模型的最终性能[8, 9]。一些最近提出的ConvNets[86, 48]用LayerNorm(LN)替换了BN,LN在Transformers[38]和Metaformer架构[154]中得到了广泛应用,并在各种场景中取得了相对较好的性能。在这里,我们在ImageNet-1K上对MogaNet中的归一化(Norm)层进行了消融研究,如表A6所示。如ConvNeXt[86]中所述,在每个块内(within)和每个阶段后(after)使用的Norm层具有不同的效果。因此,我们分别研究了它们。表A6显示,在两个地方都使用BN的性能优于在“after”位置使用LN和在“within”位置使用BN,除了分辨率为224^2的MogaNet-T。而在两个地方都使用LN的性能最差。因此,出于两个原因,我们在提出的MogaNet中使用BN作为默认的Norm层:(i)对于纯卷积操作符,将卷积操作与每个阶段内的BN相结合的规则对于现代ConvNets仍然是有用的。(ii)尽管在每个阶段后使用LN可能有助于稳定Transformers和混合模型的训练过程,并且有时可以为ConvNets带来良好的性能,但在纯卷积模型中在每个阶段后采用BN仍然可以获得更好的性能。此外,我们用precise BN(pBN)[144]替换了BN,pBN是BN的一种最优替代归一化策略。我们发现性能有轻微的提升(大约0.1%),特别是当MogaNet-S/B采用EMA策略(默认设置)时,这表明我们可以通过先进的BN进一步改进MogaNet。如ConvNeXt中所述,EMA可能会严重损害使用BN的模型的性能。这种现象可能是由于在大型模型中,使用EMA估计的BN统计信息不稳定和不准确所导致的,当对模型参数使用另一个EMA时,这种情况会恶化。我们通过在训练过程中将EMA衰减率从0.9指数增加到0.9999来解决这个困境,这与基于动量的对比学习方法[15, 7](例如BYOL[46])中的做法类似。这个问题也可以通过先进的BN变体[58, 144]来解决。
C.5、轻量级模型的优化训练设置
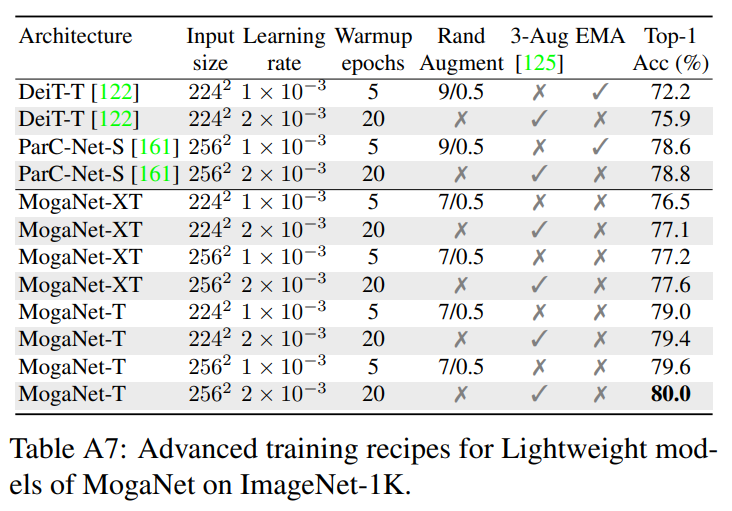
为了充分发挥我们MogaNet轻量级模型的全部能力,我们根据RSB A2 [138]和DeiTIII [125]对MogaNet-XT/T的基本训练设置进行了优化。与表A2中提供的默认设置相比,我们仅调整了学习率和增强策略以加快收敛速度,同时保持其他设置不变。如表A7所示,当使用较大的学习率 2 × 1 0 − 3 2 \times 10^{-3} 2×10−3 和3-Augment [125] 而无需复杂设计时,MogaNet X T / T \mathrm{XT} / \mathrm{T} XT/T 获得了 + 0.4 ∼ 0.6 % +0.4 \sim 0.6 \% +0.4∼0.6% 的提升。基于高级设置,MogaNet在 22 4 2 224^{2} 2242 输入分辨率下与以前的方法相比取得了显著的性能提升,例如,MogaNet-T比DeiT-T [122] 提高了 + 3.5 % +3.5 \% +3.5%,比Parc-Net-S [161] 提高了 + 1.2 % +1.2 \% +1.2%。特别是,MogaNet-T在 25 6 2 256^{2} 2562 分辨率下达到了 80.0 % 80.0 \% 80.0% 的top1准确率,优于原始论文中报告的DeiT-S的 79.8 % 79.8 \% 79.8%,而MogaNet-XT在 22 4 2 224^{2} 2242 分辨率下仅使用 3 M 3 \mathrm{M} 3M 参数,在优化训练方案下比DeiT-T提高了 1.2 % 1.2 \% 1.2%。

D、更多对比实验
D.1、在ImageNet-1K上的快速训练
除了第5.1节,我们进一步提供了在ImageNet 1K上进行100和300个epoch训练的对比结果。对于100个epoch的训练,我们为所有方法采用了原始的RSB A3 [138]设置,该设置采用LAMB [153]优化器和小型训练分辨率 16 0 2 160^{2} 1602。我们为所有架构搜索了基本学习率集合 { 0.006 , 0.008 } \{0.006,0.008\} {0.006,0.008},并为基于Transformer的网络采用了梯度裁剪。对于300个epoch的训练,我们报告了RSB A2 [138]对于经典CNN或Transformers或现代ConvNets的原始设置的结果。在表A15中,当与参数大小相似的模型进行比较时,我们提出的MogaNet-XT/T/S/B在100和300个epoch的训练中都实现了最佳性能。100个epoch训练的结果表明,MogaNet比各种类型的先前架构具有更快的收敛速度。例如,MogaNet-T比EfficientNetB0和DeiT-T高出 2.4 % 2.4 \% 2.4% 和 8.7 % 8.7 \% 8.7%,MogaNet-S比Swin-T高出 3.4 % 3.4 \% 3.4%,而MogaNet-B比Swin-S高出 2.0 % 2.0 \% 2.0%。请注意,ConvNeXt变体具有很大的收敛速度,例如,ConvNeXt-S实现了 81.7 % 81.7 \% 81.7% 的准确率,超过了Swin-S 1.5 % 1.5\% 1.5%,并且最近提出的ConvNet HorNet S_{7 \times 7} 准确率高出 0.5 % 0.5\% 0.5%,参数量相似。但是,我们提出的MogaNet比ConvNet收敛更快,例如,MogaNet-S在参数相似的情况下比ConvNeXt-T高出 2.3 % 2.3 \% 2.3%,而MogaNet-B/L仅使用 44 ∼ 50 % 44 \sim 50 \% 44∼50% 的参数就达到了与ConvNeXt-B/L相当的性能。
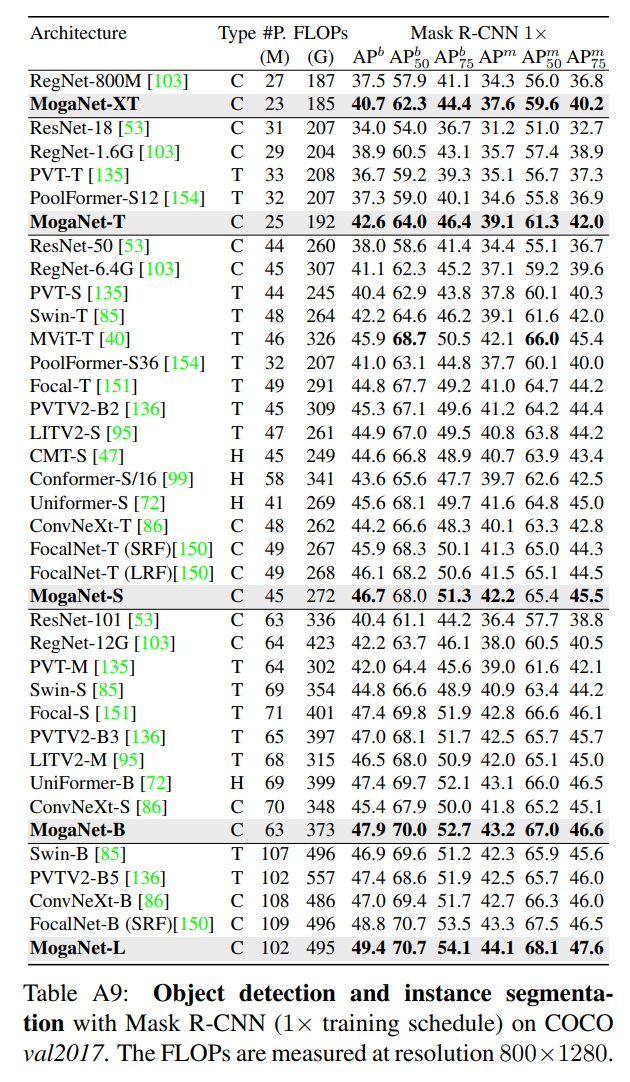
D.2、在COCO上的检测和分割结果
除了第5.2节,我们提供了使用RetinaNet、Mask R-CNN和Cascade Mask R-CNN在COCO上的物体检测和实例分割任务的完整结果。如表A8和表A9所示,使用MogaNet变体的RetinaNet或Mask R-CNN在1倍训练计划下优于现有模型。例如,使用MogaNet-T/S/B/L的RetinaNet实现了45.8/47.7/48.7的 A P b \mathrm{AP}^{b} APb,比PVT-T/S/M和PVTV2-B1/B2/B3/B5高出4.7/4.6/5.8和0.3/1.2/1.7/2.6的 A P b \mathrm{AP}^{b} APb;使用MogaNet-S/B/L的Mask R-CNN实现了46.7/47.9/49.4的 A P b \mathrm{AP}^{b} APb,在参数和计算量相似的情况下超过了Swin-T/S/B和ConvNeXt-T/S/B的4.5/3.1/2.5和2.5/2.5/2.4。值得注意的是,MogaNet-XT/T在参数更少、FLOPs更低的情况下实现了更好的检测结果,而MogaNet-T甚至超过了某些Transformer,如Swin-S和PVT-S。例如,使用MogaNet-T的Mask R-CNN比Swin-T提高了0.4的 A P b \mathrm{AP}^{b} APb,并仅使用大约2/3的参数就超过了PVT-S的1.3的 A P m \mathrm{AP}^{m} APm。如表A10所示,使用多尺度(MS)和高级增强的3倍训练计划时,Cascade Mask R-CNN与MogaNet变体仍然实现了最先进的检测和分割结果。例如,MogaNet-L/XL实现了53.3/56.2的 A P b \mathrm{AP}^{b} APb和46.1/48.8的 A P m \mathrm{AP}^{m} APm,在参数和FLOPS相似的情况下,比Swin-B/L和ConvNeXt-B/L提高了1.4/2.3和0.6/1.4的 A P b \mathrm{AP}^{b} APb。
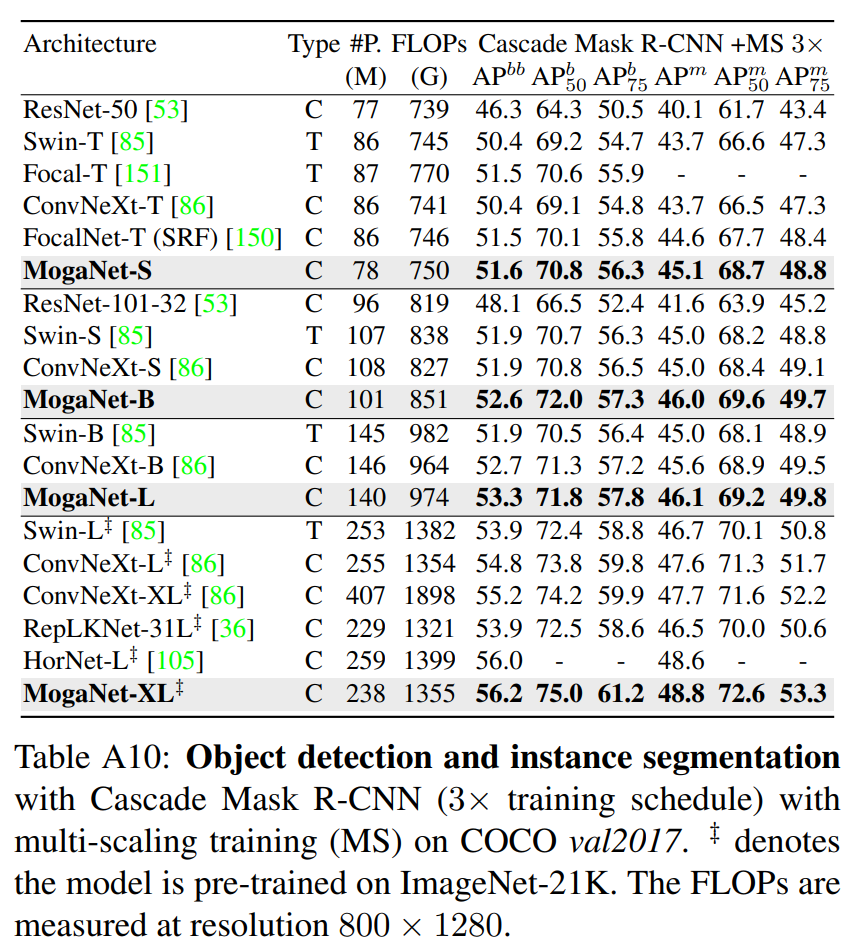
D.3、ADE20K上的语义分割结果
除了第5.2节的内容外,我们还提供了在ADE20K上基于UperNet的语义分割综合对比结果。如表A11所示,与著名的Transformer、混合和卷积模型相比,配备MogaNet的UperNet在广泛的参数规模范围内都展现出了最先进的性能。对于轻量级模型,MogaNet-XT/T在参数和计算量(FLOPs)更少的情况下,显著地提升了ResNet18/50的性能。对于中等规模的模型,MogaNet-S/B达到了49.2/50.1的 m I o U s s \mathrm{mIoU}^{ss} mIoUss(语义分割的平均交并比),这优于最近提出的ConvNets。例如,与使用相似参数的HorNet-T相比,提升了1.1;与使用少了17M参数的SLaK-S相比,提升了0.7。对于大型模型,MogaNet-L/XL在使用更少参数的情况下,分别超过了Swin-B/L和ConvNeXt-B/L达1.2/1.9和1.8/0.3的 m I o U s s \mathrm{mIoU}^{ss} mIoUss。这些结果表明,无论模型大小如何,MogaNet都能在各种参数规模下提供卓越的语义分割性能。
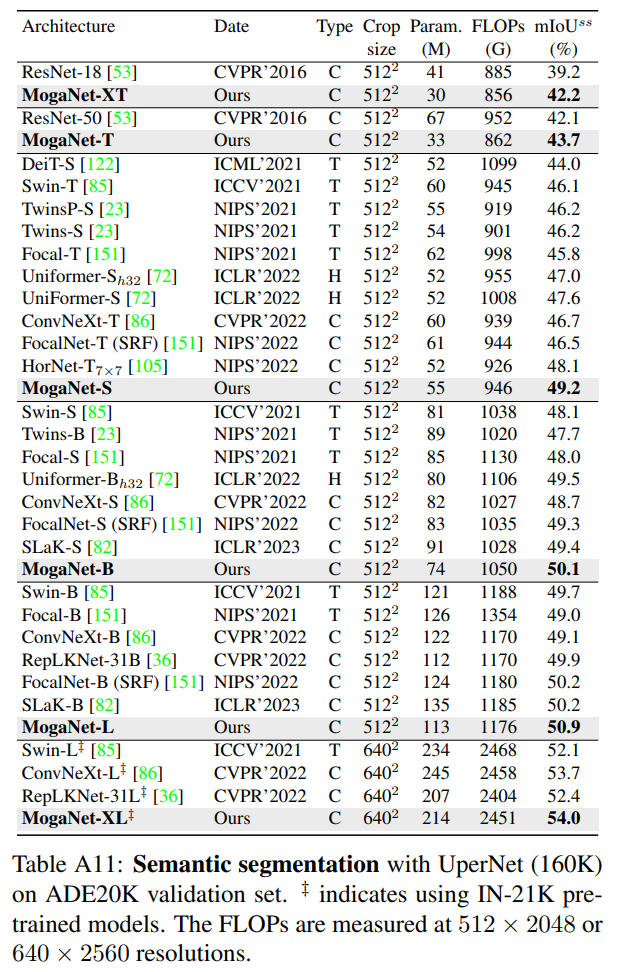
D.4、COCO上的2D人体姿态估计结果
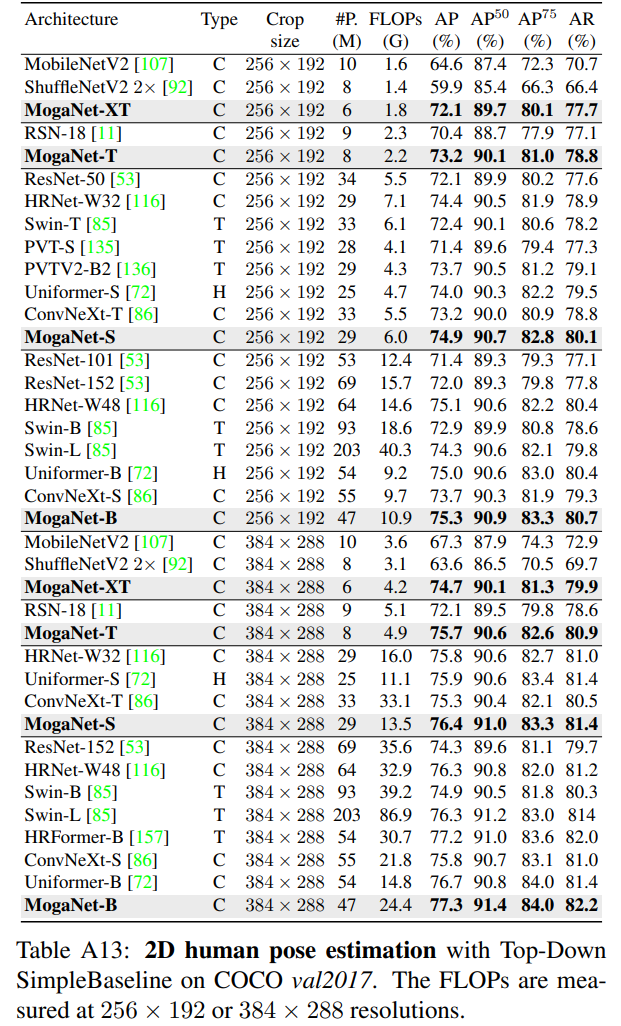
除了第5.2节的内容外,我们还提供了在COCO数据集上基于Top-Down SimpleBaseline的2D人体关键点估计的综合实验结果。如表A13所示,与两种不同分辨率的流行架构相比,MogaNet的变种取得了具有竞争力的或最先进的性能。对于轻量级模型,MogaNet-XT/T在使用相似参数和计算量(FLOPs)的同时,显著提高了现有模型的性能。此外,MogaNet-S/B在使用256x192和384x288两种分辨率的情况下,分别达到了74.9/75.3和76.4/77.3的AP(平均精度),这几乎是以一半的参数和计算量超过了Swin-B/L的2.0/1.0和1.5/1.0的AP。
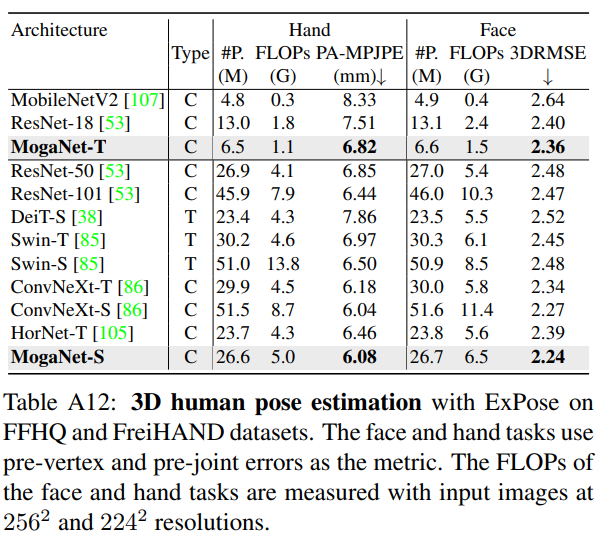
D.5、3D人体姿态估计结果
除了第5.2节的内容外,我们还基于ExPose [22]评估了流行的ConvNets和MogaNet在3D人体姿态估计任务上的表现。如表A12所示,MogaNet以高效的参数使用和计算开销实现了较低的回归误差。与轻量级架构相比,MogaNet-T在手部和面部重建任务上分别实现了6.82 MPJPE(平均每关节位置误差)和2.36 3DRMSE(3D根均方误差),相较于ResNet-18和MobileNetV2 1×分别提升了1.29/0.04和1.51/0.28。与参数规模约为25-50M的模型相比,MogaNet-S超过了ResNet-101和ConvNeXt-T,以相对较小的参数和计算量(例如,在FFHP上为27M/6.5G vs 52M/11.4G)实现了与ConvNeXt-S相当的结果。值得注意的是,在面部估计任务上,一些参数更多的主干网络的表现甚至不如其轻量级变体(例如,ResNet-50和Swin-S),而MogaNet-S仍然取得了更好的性能,达到了2.24的3DRMSE。
D.6、Moving MNIST上的视频预测结果
除了第5.2节,我们还通过用架构块替换SimVP中的隐藏转换器来验证各种架构的视频预测性能。所有模型都使用相同数量的网络块,并具有相似的参数和FLOPs。如表A14所示,与基于Transformer和Metaformer的架构相比,纯ConvNets通常实现更低的预测误差。值得注意的是,在训练200个epoch时,在SimVP中使用MogaNet块可以显著提高SimVP基准的6.58/13.86 MSE/MAE,并优于ConvNeXt和HorNet的1.37和4.07 MSE。在扩展的2000个epoch训练设置中,MogaNet也保持了最佳性能。