Problem: 53. 最大子数组和

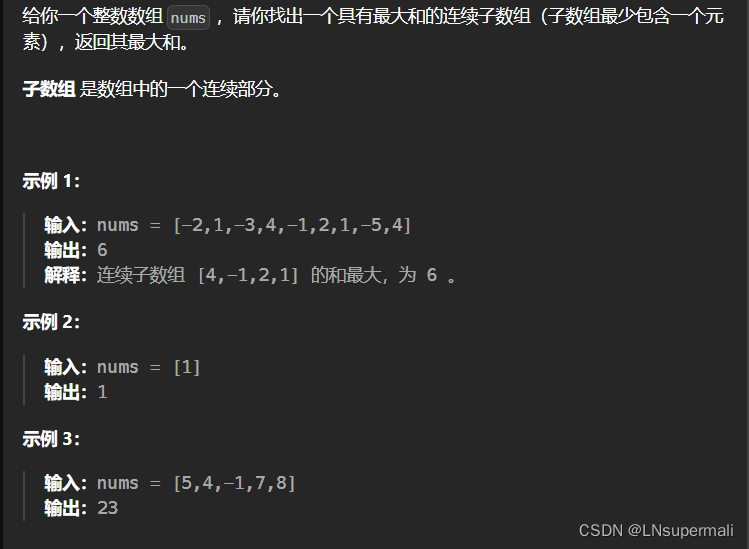
题目描述

思路及解法

思路1:滑动窗口

1.为求出最大连续的子数组和,我们逻辑上假设有一个窗口在原数组上滑动,
欲求出最大连续,则需要保证窗口中的所有元素和最起码大于0;
2.即当当前窗口中的元素值的和小于0时,直接将其窗口舍弃,并在当前位置重新开一个新的窗口;
3.在实际操作中我们可以直接利用一个值(sum)进行累加操作,并判断其正负性;同时再记录一个值maxSum用于求出最大的连续子数组和

思路2:动态规划

1.用一个数组dp记录以第$i$个数结尾时的最大子数组和;
2.欲得出当前的最大子数组和,则需要比较*dp[i - 1] + nums[i]的值与nums[i]*的值谁更大;
3.即得出动态转移方程:dp[i] = max(dp[i - 1] + nums[i], nums[i])
4.求出dp数组中的最大值即可

复杂度

思路1:滑动窗口
时间复杂度:

$O(n)$;其中$n$为原数组$nums$的大小

空间复杂度:

$O(1)$

思路2:动态规划
时间复杂度:

$O(n)$

空间复杂度:

$O(n)$

Code

思路1:滑动窗口

class Solution {
public:
    /**
     * Slider windows
     * @param nums Given array
     * @return int
     */
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        int maxSum = INT_MIN;
        int sum = 0;
        for (int i = 0; i < n; ++i)  {
            if (sum < 0) {
                sum = 0;
            }
            sum += nums[i];
            if (sum > maxSum) {
                maxSum = sum;
            }
        }
        return maxSum;
    }
};

思路2:动态规划

class Solution {
public:
    /**
     * Dynamic programing
     * @param nums Given arr
     * @return int
     */
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n + 1);
        dp[0] = nums[0];
        for (int i = 1; i < n; ++i) {
            dp[i] = max(dp[i - 1] + nums[i], nums[i]);
        }
        int max = INT_MIN;
        for (int i = 0; i < n; ++i) {
            if (dp[i] > max) {
                max = dp[i];
            } 
        }
        return max;
    }
};