这是树的第12篇算法，力扣链接。

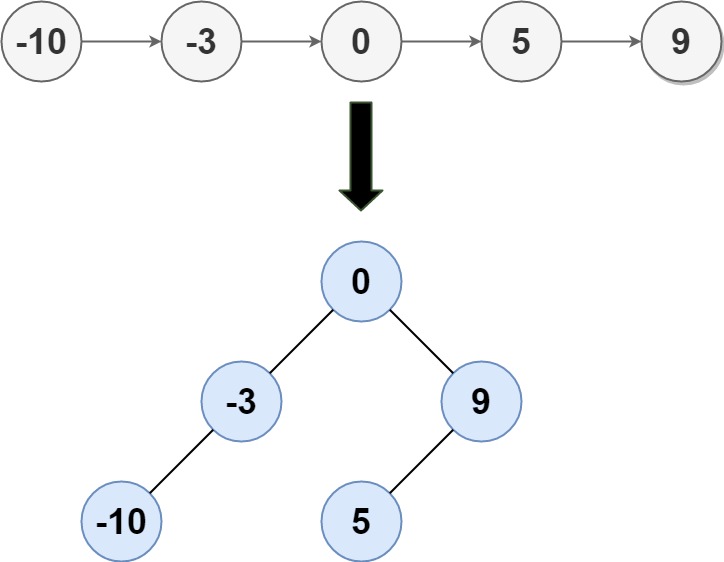
给定一个单链表的头节点  head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

示例 1:

输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

最暴力的做法是转换为数组去做有序数组构建二叉树：

func sortedListToBST(head *ListNode) *TreeNode {
	if head == nil {
		return nil
	}
	nodeList := make([]int, 0)
	for head != nil {
		nodeList = append(nodeList, head.Val)
		head = head.Next
	}
	result := &TreeNode{
		Val: nodeList[(len(nodeList))/2],
	}
	result.Left = sortedArrayToBST(nodeList[:(len(nodeList))/2])
	result.Right = sortedArrayToBST(nodeList[(len(nodeList))/2+1:])
	return result
}

func sortedArrayToBST(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	if len(nums) == 1 {
		return &TreeNode{Val: nums[0]}
	}
	result := &TreeNode{Val: nums[len(nums)/2]}
	result.Left = sortedArrayToBST(nums[:len(nums)/2])
	result.Right = sortedArrayToBST(nums[len(nums)/2+1:])
	return result
}

既然递归的核心逻辑是找中点，链表的找中点逻辑也可以用上：

func sortedListToBST(head *ListNode) *TreeNode {
	return buildBST(head, nil)
}

func buildBST(left, right *ListNode) *TreeNode{
	if left == right {
		return nil
	}
	mid := getMedian(left, right)
	root := &TreeNode{mid.Val, nil, nil}
	root.Left = buildBST(left, mid)
	root.Right = buildBST(mid.Next, right)
	return root
}

func getMedian(left, right *ListNode) *ListNode {
	fast, slow := left, left
	for fast != right && fast.Next != right {
		fast = fast.Next.Next
		slow = slow.Next
	}
	return slow
}