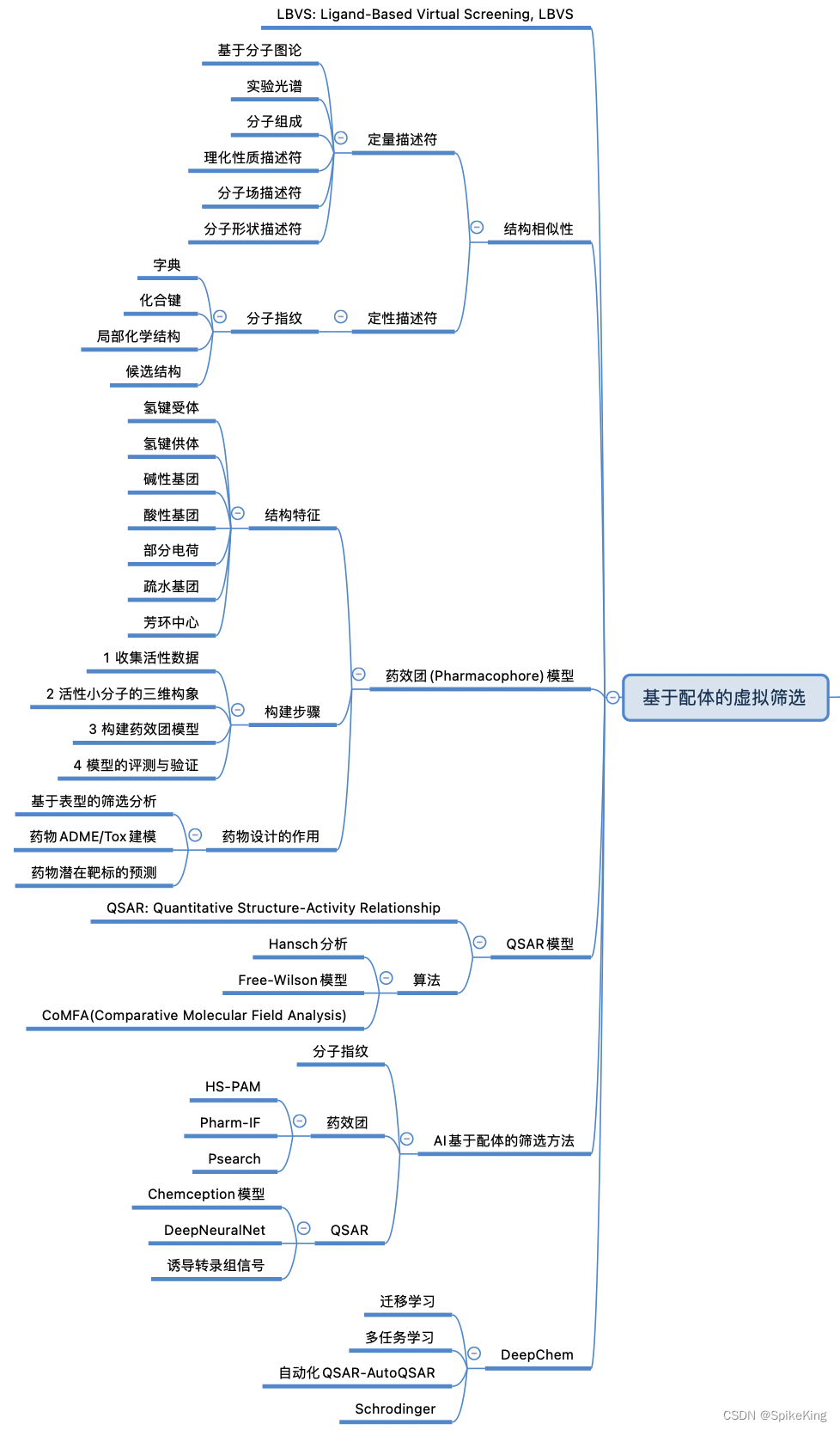
互感

互感是一个线圈磁场与另一个线圈的相互作用，因为它在相邻线圈中感应出电压。

1、概述

互感是两个磁耦合线圈之间的电路参数，定义了一个线圈产生的时变磁通量被感应到相邻的第二个线圈中的比率。

之前我们看到，电感器由于其自身线圈匝周围的磁场变化而产生自感电动势。 当在电流变化的同一电路中感应出该电动势时，这种效应称为自感 ($L$)。

然而，当电动势被感应到位于同一磁场内的相邻线圈中时，电动势被称为磁感应、感应感应或互感应感应，符号（$M$）。 然后，当两个或多个线圈通过公共磁通量磁连接在一起时，它们就具有互感特性。

互感是变压器、电机、发电机和任何其他与另一个磁场相互作用的电气元件的基本工作原理。 然后我们可以将互感定义为一个线圈中流动的电流在相邻线圈中感应出电压。

但互感也可能是一件坏事，因为线圈的“杂散”或“漏”电感会通过电磁感应干扰另一个相邻组件的运行，因此可能需要对地电位进行某种形式的电气屏蔽。

将一个线圈连接到另一个线圈的互感量很大程度上取决于两个线圈的相对位置。 如果一个线圈放置在另一个线圈旁边，使得它们的物理距离很小，那么第一个线圈产生的几乎所有磁通量都会与第二个线圈的线圈匝相互作用，从而感应出相对较大的电动势，从而产生一个 互感值大。

同样，如果两个线圈彼此距离较远或角度不同，则从第一个线圈到第二个线圈的感应磁通量将较弱，产生更小的感应电动势，因此互感值也更小。 因此，互感的影响很大程度上取决于两个线圈的相对位置或间距 ($S$)，这将在下面进行演示。

线圈之间的互感

通过将两个线圈放置在公共软铁芯上或通过增加变压器中任一线圈的匝数，可以大大增加两个线圈之间存在的互感。

如果两个线圈在一个共同的软铁芯上紧密地缠绕在另一个线圈的顶部，则据说它们之间存在整体耦合，因为由于磁通泄漏而造成的任何损耗都将非常小。 然后假设两个线圈之间存在完美的磁链，则它们之间存在的互感可以为：

其中：

• ${\mu }_o$ 是自由空间的渗透性 ($4.\pi .10^{-7})$
• $\mu r$ 是软铁芯的相对磁导率
• $N$ 是线圈匝数
• $A$ 的横截面积为 $m^2$
• $\ell$ 是线圈长度（以米为单位）

2、互感

这里，第一线圈 $L_1$ 中流动的电流在其自身周围建立了一个磁场，其中一些磁场线穿过第二线圈 $L_2$，从而产生互感。 线圈一的电流为 $I_1$，匝数为 $N_1$，线圈二的电流为 $N_2$ 匝。 因此，线圈二相对于线圈一存在的互感 $M_{12}$ 取决于它们相对于彼此的位置，计算公式为：

同样，当电流流过线圈二时，线圈一的磁通链结 $L_1$ 与线圈一上流过相同电流时的磁通链结线圈 $L_2$ 完全相同，则线圈一相对于线圈二的互感 定义为$M_{21}$。 无论两个线圈的尺寸、匝数、相对位置或方向如何，该互感都是真实的。 因此，我们可以将两个线圈之间的互感写为：$M_{12}=M_{21}=M$。

然后我们可以看到，自感将电感器表征为单个电路元件，而互感表示两个电感器或线圈之间某种形式的磁耦合，具体取决于它们的距离和布置，希望我们从电磁体教程中记住，自感 每个单独线圈的电感由下式给出：

通过将上述两个方程相乘，两个线圈之间存在的互感 M 可以用每个线圈的自感来表示。

为我们提供了两个线圈之间互感的最终且更常见的表达式：

线圈之间的互感

然而，上式假设两个线圈 $L_1$ 和 $L_2$ 之间的漏磁为零且磁耦合为 100%。 现实中总会因漏电和位置而产生一些损耗，因此两个线圈之间的磁耦合永远不可能达到或超过100%，但在一些特殊的电感线圈中可以变得非常接近这个值。

如果总磁通中的一些与两个线圈交链，则该磁通量可以被定义为线圈之间的总可能磁通的一部分。 这个分数值称为耦合系数，用字母 $k$ 表示。

3、耦合系数

通常，两个线圈之间存在的电感耦合量表示为 0 到 1 之间的分数，而不是百分比 (%) 值，其中 0 表示零或无电感耦合，1 表示完全或最大电感耦合。

换句话说，如果 $k=1$，则两个线圈完美耦合；如果 $k>0.5$，则两个线圈被称为紧密耦合；如果 $k<0.5$，则两个线圈被称为松散耦合。 然后可以修改上面假设完美耦合的方程，以考虑耦合系数 $k$，并给出如下：

当耦合系数 $k$ 等于 1（单位），使得一个线圈的所有磁通线切割第二个线圈的所有匝数，即两个线圈紧密耦合在一起时，产生的互感将 等于线圈的两个单独电感的几何平均值。

另外，当两个线圈的电感相同且相等时，$L_1$ 等于 $L_2$，两个线圈之间存在的互感将等于一个单个线圈的值，因为两个相等值的平方根等于 1 如图所示的单个值。

4、互感示例1

自感分别为 75mH 和 55mH 的两个电感器彼此相邻地放置在公共磁芯上，以便来自第一个线圈的 75% 的磁通线切割第二个线圈。 计算两个线圈之间存在的总互感。

5、互感示例2

当两个电感分别为5H和4H的线圈均匀地绕在非磁芯上时，发现它们的互感为1.5H。 计算之间存在的耦合系数。

在下一篇关于电感器的文章中，我们将研究串联电感器，以及这种组合对电路互感、总电感及其感应电压的影响。