坚持刷题｜二叉树的直径

news2024/9/22 5:14:37

文章目录

题目
考察点
代码实现
实现总结
方便用迭代的方式实现吗？
- 迭代实现
- 迭代实现总结

Hello，大家好，我是阿月。坚持话题，老年痴呆追不上我，今天还有时间，那就再来一题吧：二叉树的直径

题目

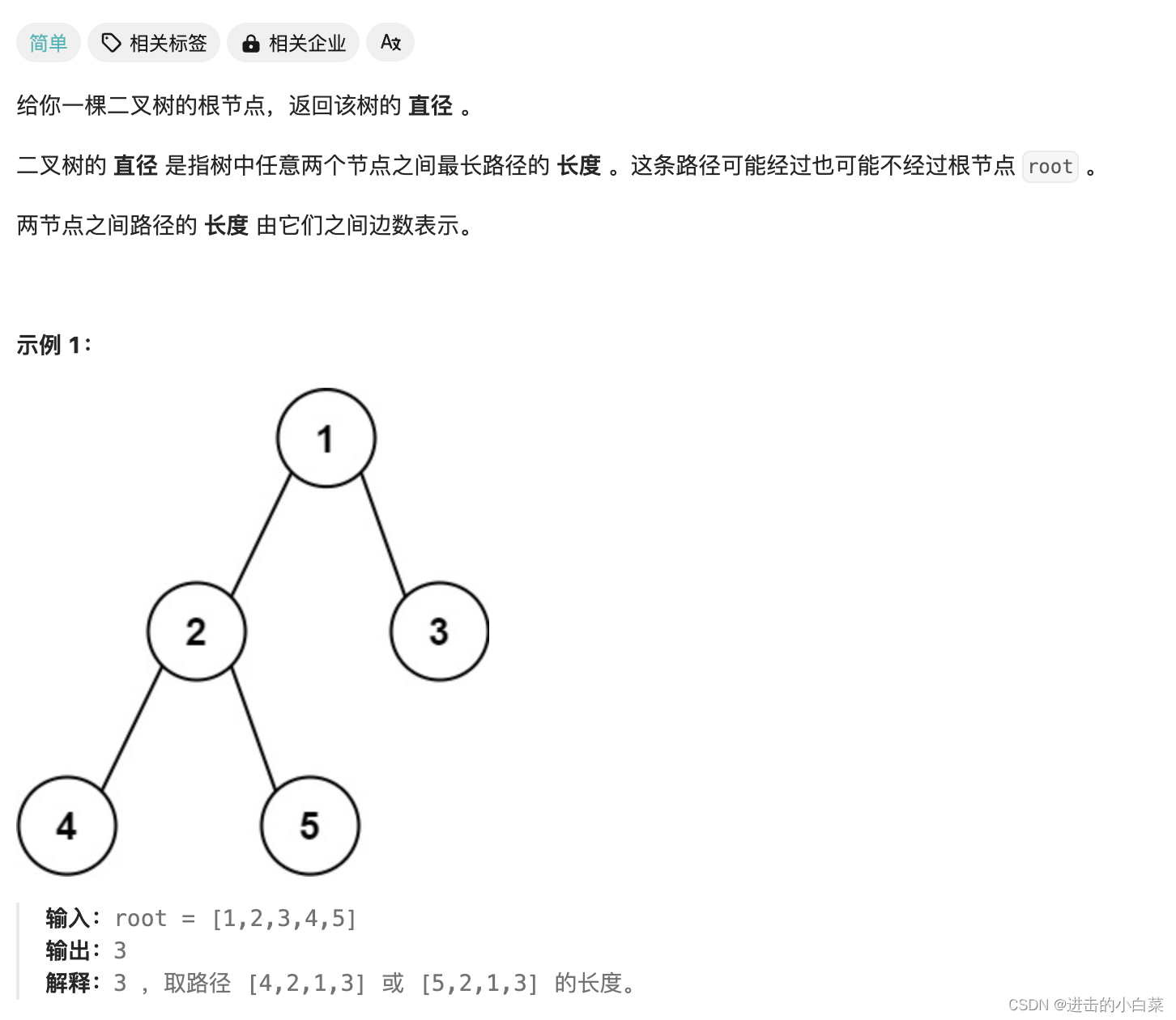
543.二叉树的直径
在这里插入图片描述

考察点

理解二叉树的结构和直径的定义。
理解直径的定义，即任意两个节点之间最长路径的长度。
能够利用数据结构合理的设计出递归算法并实现。
算法的正确性和高效性是非常重要的考察点。

代码实现

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class BinaryTreeDiameter {
    int diameter;

    public int diameterOfBinaryTree(TreeNode root) {
        diameter = 0;
        depth(root);
        return diameter;
    }

    private int depth(TreeNode node) {
        if (node == null) return 0;

        int leftDepth = depth(node.left);
        int rightDepth = depth(node.right);

        diameter = Math.max(diameter, leftDepth + rightDepth);

        return Math.max(leftDepth, rightDepth) + 1;
    }

    public static void main(String[] args) {
        // 构建测试用的二叉树
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        BinaryTreeDiameter solution = new BinaryTreeDiameter();
        System.out.println("Diameter of the binary tree: " + solution.diameterOfBinaryTree(root));
    }
}

实现总结

方法diameterOfBinaryTree，用来计算二叉树的直径。
depth方法被用来计算节点的深度，并通过计算左右子树的深度，更新直径的值。
最后，在main方法中构建一个测试用的二叉树，并输出其直径。
这个实现实际上借鉴了坚持刷题｜二叉树的最大深度的思想。
- 在计算二叉树的直径时，需要获取每个节点的左子树和右子树的深度，并结合起来计算直径。
- 在计算二叉树的最大深度时，也是递归地计算左子树和右子树的深度，然后取最大值并加上根节点的深度来得到整棵树的深度。
时间复杂度：O(N)，其中 N是二叉树中节点的数量。
- 在深度优先搜索（DFS）的过程中，遍历了二叉树的每个节点一次。
- 对于每个节点，都需要计算其左子树和右子树的深度，这个操作的时间复杂度是 O(1) ，因为每个节点只需要常数时间来计算。
- 因此，总的时间复杂度是所有节点的数量，即 O(N)。

方便用迭代的方式实现吗？

当涉及到计算二叉树直径时，通常更适合使用递归而不是迭代。尽管可以通过一些技巧来使用迭代，但通常会更加复杂且不直观。这是因为直径的计算涉及到节点的深度，而深度优先搜索（DFS）的自然实现是通过递归来完成的。

迭代实现

import java.util.Stack;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class BinaryTreeDiameterIterative {
    public int diameterOfBinaryTree(TreeNode root) {
        if (root == null) return 0;
        
        int diameter = 0;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            int leftDepth = maxDepth(node.left);
            int rightDepth = maxDepth(node.right);
            diameter = Math.max(diameter, leftDepth + rightDepth);
            
            if (node.left != null) stack.push(node.left);
            if (node.right != null) stack.push(node.right);
        }
        
        return diameter;
    }
    
    private int maxDepth(TreeNode node) {
        if (node == null) return 0;
        
        int leftDepth = 0, rightDepth = 0;
        Stack<TreeNode> nodeStack = new Stack<>();
        Stack<Integer> depthStack = new Stack<>();
        nodeStack.push(node);
        depthStack.push(1);
        
        while (!nodeStack.isEmpty()) {
            TreeNode currNode = nodeStack.pop();
            int currDepth = depthStack.pop();
            if (currNode.left != null) {
                nodeStack.push(currNode.left);
                depthStack.push(currDepth + 1);
            }
            if (currNode.right != null) {
                nodeStack.push(currNode.right);
                depthStack.push(currDepth + 1);
            }
            leftDepth = Math.max(leftDepth, currDepth);
        }
        
        return leftDepth;
    }

    public static void main(String[] args) {
        // 构建测试用的二叉树
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        BinaryTreeDiameterIterative solution = new BinaryTreeDiameterIterative();
        System.out.println("Diameter of the binary tree: " + solution.diameterOfBinaryTree(root));
    }
}