1. 设计要求
以图形界面的方式设计一套程序,该程序可以实现以下功能:
- 从输入框输入单个或多个概率,然后使用者可以通过相关按钮的点击求解相应的对数,自信息以及信息熵
- 程序要能够实现马尔可夫信源转移概率矩阵的输入并且可以计算该马尔可夫信源在每一个状态下每输出一个符号的平均信息量,稳态概率以及最后的信息熵。
- 结果在在界面中直接呈现
2. 设计过程
首先进行图形界面的设计,根据要求界面中应该包括相关标签,输入,输出以及对应按钮,单行少量输入可以采用普通TextBox控件,多行输入可以采用RichTextBox控件,输出要有对应的标签,为了美观,将输出控件原始标签删除修改为空白,只有输出值才会出现
本实验总体界面设计如图一所示:
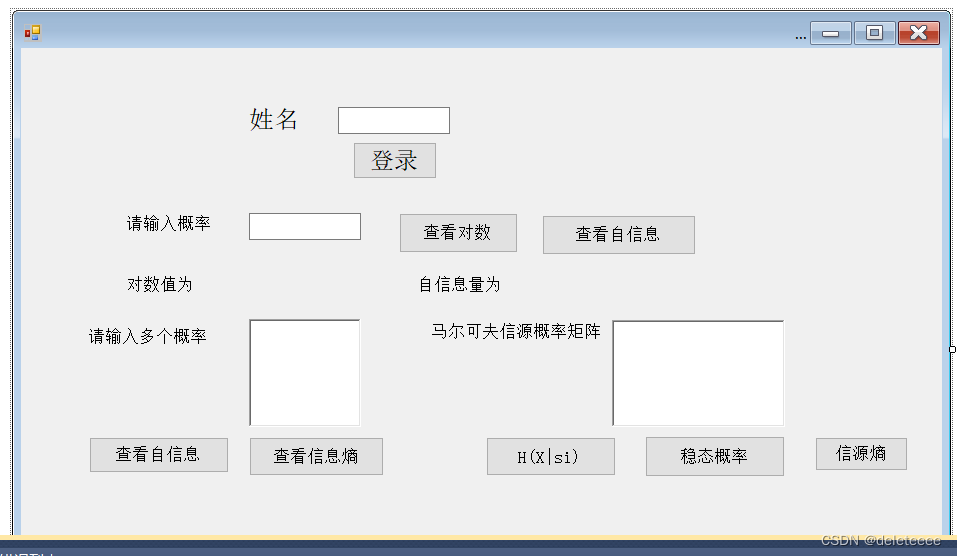
图1 设计图形界面
接下来对于点击不同按钮产生的事件进行设计:
由于对数值以及自信息设计过程相对简单,以下着重介绍信息熵以及马尔可夫信源设计过程。
查看信息熵按钮代码实现:
private void button5_Click(object sender, EventArgs e)
{
string[] a = new string[richTextBox1.Lines.Length];//定义数组,设定空间大小为输入框的行数
double[] px = new double[richTextBox1.Lines.Length];
double[] y = new double[richTextBox1.Lines.Length];
double z = 0;
for (int i = 0; i < richTextBox1.Lines.Length; i++)
{
a[i] = richTextBox1.Lines[i];//获取每一行的值,存入数组a中
px[i] = Convert.ToDouble(a[i]);//将字符串转换为可计算的double类型
y[i] = Math.Log(1 / px[i], 2);
z = z + px[i] * y[i];//计算信息熵
}
label8.Text = Convert.ToString(Math.Round(z, 2));//结果转换成字符串形式再输出
}在相关按钮中输入上述所示代码即可实现信息熵的计算
在设计马尔可夫信源时,考虑到其概率矩阵更便于观察,所以需要通过输入概率矩阵然后提取相关的概率来进行计算。
要想求信源熵,我们得知道稳态概率值以及在si状态下每输出一个符号的平均信息量,最后对状态取统计平均后得到信源每输出一个符号的信息量,即马尔可夫信源的熵。
对于H(X|si)的值可以直接通过计算得到,求法如下:
private void button6_Click(object sender, EventArgs e)
{
int a = richTextBox2.Lines.Length;
double[,] p = new double[a, a];
char[] sp = new char[3] { ' ', '\t', '\n' };
string[] str1 = new string[100];
str1 = richTextBox2.Text.Split(sp);
label10.Text = "";
for (int i = 0; i < a; i++)
{
double h = 0;
for (int j = 0; j < a; j++)
{
p[i, j] = Convert.ToDouble(str1[i * a + j]);
if (p[i, j] == 0)
{
p[i, j] = 1;
}
h = h + p[i, j] * Math.Log(1 / p[i, j], 2);
}
label10.Text += Convert.ToString(Math.Round(h, 3)) + '\n';
}
}对于稳态概率的值无法直接进行计算得到,因为需要解方程,我对此采用的方法为高斯列选主元消元迭代求解。
首先将概率矩阵进行转置,然后每一行都可以列方程,为使求解更加简便,将方程移项,等式左边为未知数,右边为一个常数,例如初始概率矩阵第一列为0.1 0.5 0 这三个数,转置后可列方程组W1=0.1*W1+0.5*W2+0*W3,移相后为-0.9*W1+0.5*W2+0*W3=0,而在数组中即为[-0.9 0.5 0 0],而对于已知方程概率和W1+W2+W3=1在数组中形式为[1 1 1 1]。
处理后代码如下:
//以下a为处理后的矩阵,b为每一行方程等式右边的常数值
double[] b = new double[n];
for (int i = 0; i < n; i++)
{
b[i] = a[i, n];//将最后一列(方程右边常数值)存入数组b中
}
for (int k = 0; k < n - 1; k++)
{
//找每一列主元,最开始我们选k行k列的为最大
max = Math.Abs(a[k, k]);//最大元值
maxp = k;//最大元列的下标
for (int p = k + 1; p < n; p++)
{
if (Math.Abs(a[p, k]) > max)
{
max = Math.Abs(a[p, k]);
maxp = p;
}
}
if (maxp != k)
{
//需要交换两行
double[] tmp = new double[n];
for (int i = 0; i < n; i++)
{
tmp[i] = a[maxp, i];
a[maxp, i] = a[k, i];
a[k, i] = tmp[i];
}
double tmpp;
tmpp = b[k];
b[k] = b[maxp];
b[maxp] = tmpp;
}
for (int i = k + 1; i < n; i++)
{
for (int j = k + 1; j < n; j++)
{
a[i, j] -= a[k, j] * a[i, k] / a[k, k];
}
b[i] -= b[k] * a[i, k] / a[k, k];
}
}
x[n - 1] = b[n - 1] / a[n - 1, n - 1];
for (int k = n - 2; k > -1; k--)
{
double sum1 = 0;
for (int j = k + 1; j < n; j++)
{
sum1 += a[k, j] * x[j];
}
x[k] = b[k] - sum1;
x[k] /= a[k, k];
}
//x即为方程的解
至此,求解信源熵的两大关键部分都已经实现,最后直接计算即可完成。
四、实验测试

图2 总体测试
从图2中可以看出:
在输入姓名后点击登录按钮将会显示欢迎,在输入概率后可以点击按钮查看它的对数或者自信息量,也可以输入多个概率并且求取信息熵,这些通过验证,结果均为正确。对于马尔可夫信源的测试,我使用的是课本上例

图3 例子
将图2中所求结果与图3中结果对比后可以看出结果正确,可以与例题中的结果一一对应上
改变数据继续验证:

图4

图5
通过图4,图5的多次验证,可以保证其与手动计算结果基本保持一致,误差可以忽略不计,实验成功。
3. 总结
按照模块分别进行设计难度不大,但是在最后实现马尔可夫信源时需要使用C#对矩阵进行处理以及运算,需要大家掌握一定的数学知识,本文的思想就是利用求解线性方程的相关算法以及高斯迭代求解方程的方法去实现。完整项目后续会上传至资源中