【题目来源】AcWing 4. 多重背包问题 I

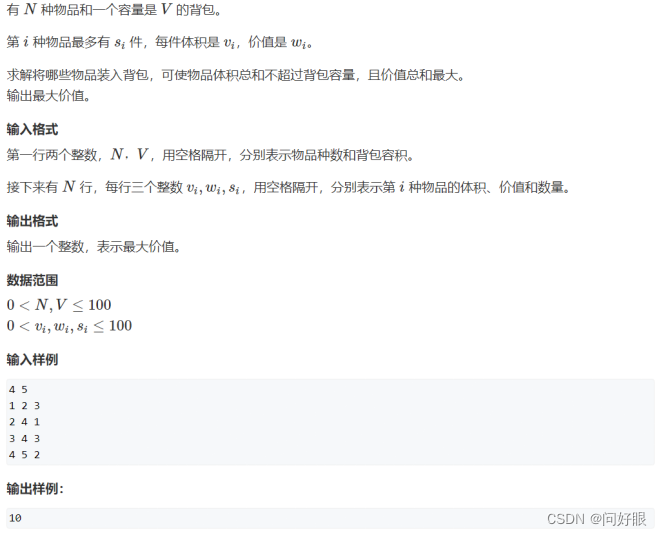
【题意分析】和完全背包问题类似，但是区别在于每一种物品的数量是有限的。
【解决方法】
1.转化为 $0/1$ 背包问题
因为每一种物品数量有限，所以将每个物品看作单独的种类，可转化为 $0/1$ 背包问题，如下表所示：

正确输入数据：

for(int i = 1; i <= n; i ++){
  int a, b, c;
  cin >> a >> b >> c;
  for(int j = 1; j <= c; j ++)
    q[++ m].v = a, q[m].w = b;
}
for(int i = 1; i <= m; i ++)
  for(int j = V; j >= q[i].v; j --)
    dp[j] = max(dp[j], dp[j - q[i].v] + q[i].w);
cout << dp[V];
//时间复杂度：O(n^3) = 10^6，1000ms能过。

2.转化为 $0/1$ 背包和完全背包问题
当有一种物品的个数，多于或等于背包完全装该种物品的数量时，此时相当于完全背包，即
$q[i].s>=V/q[i].v\Rightarrow q[i].s\ast q[i].v>=V$
当不满足时，为 $0/1$ 背包，代码如下：

int main(){
  cin >> n >> V;
  for(int i = 1; i <= n; i ++){
    cin >> q[i].v >> q[i].w >> q[i].s;
    if(q[i].s * q[i].v >= V)  //完全背包问题 
      for(int j = q[i].v; j <= V; j ++)
        dp[j] = max(dp[j], dp[j - q[i].v] + q[i].w);
    else  //0/1背包问题 
      for(int j = V; j >= q[i].v; j --)
        for(int k = q[i].s; k >= 0; k --)
          if(j >= k * q[i].v)
            dp[j] = max(dp[j], dp[j - k * q[i].v] + k * q[i].w);      
  cout << dp[V];
  return 0;
}
//时间复杂度：O(n^3) = 10^6，1000ms能过。