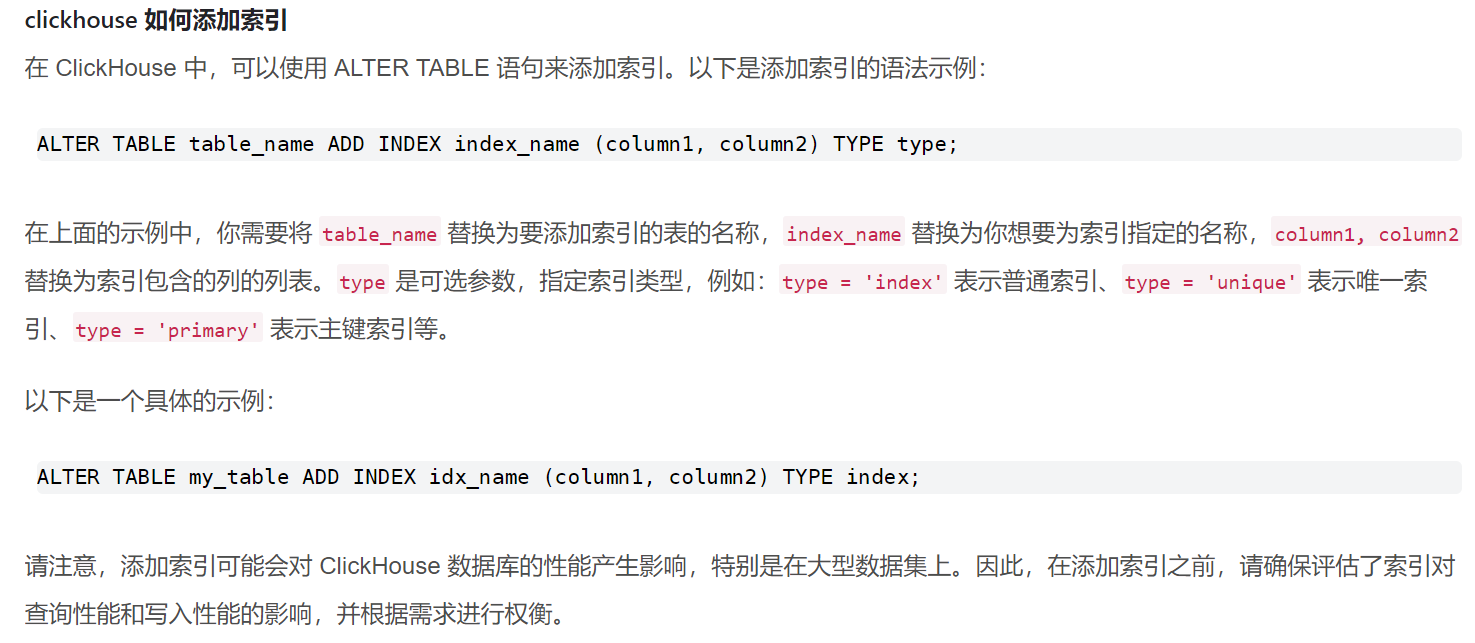
机器学习系列4-特征工程

学习内容来自：谷歌ai学习
https://developers.google.cn/machine-learning/crash-course/framing/check-your-understanding?hl=zh-cn
本文作为学习记录

自己归纳整理的思维导图

一级目录

二级目录

三级目录

1.数据集划分

1.1 将数据集划分为 训练集和测试集

将数据集划分为两个子集的概念：

• 训练集 - 用于训练模型的子集。
• 测试集 - 用于测试训练后模型的子集。
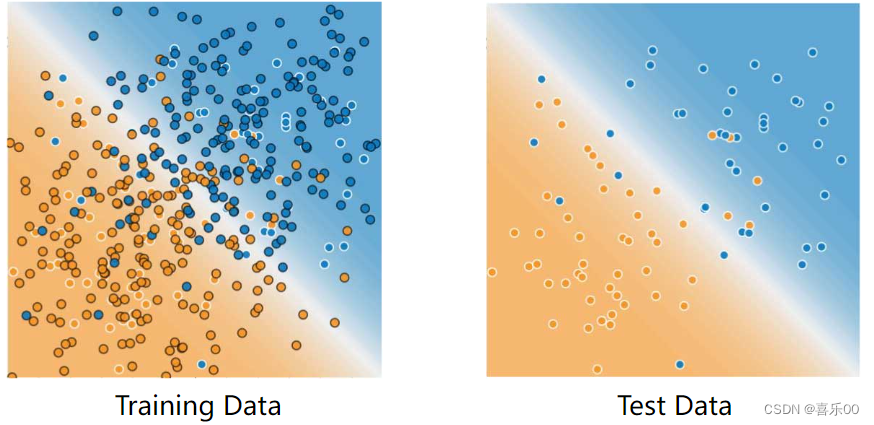
  将单个数据集划分为训练集和测试集。
  
  确保您的测试集满足以下两个条件：
• 足够大，可以得出具有统计意义的结果。
• 能代表整个数据集。也就是说，在选择测试集时，不要选择与训练集具有不同特征的测试集。
  
  切勿使用测试数据进行训练。 如果您的评估指标结果出乎意料的好，则可能表明您不小心对测试集进行了训练。例如，高准确率可能表示测试数据泄露到了训练集内。
  

1.1.1举例1：

假设某个模型使用主题行、电子邮件正文和发件人的电子邮件地址作为特征来预测电子邮件是否为垃圾邮件。
我们将数据拆分为训练集和测试集，拆分比例为 80-20。

训练完成后，该模型在训练集和测试集上的精确率均达到 99%。我们预计测试集的精确率较低，因此我们再次查看数据，发现测试集中的许多样本都与训练集中的样本重复（我们并没有忽略输入数据库中同一垃圾邮件的重复条目，然后再拆分数据）。我们无意中对部分测试数据进行了训练，因此无法再准确衡量模型泛化到新数据的程度。

1.1.2 问题1

问题1：使用测试集和训练集来推动模型开发迭代的流程。在每次迭代中，我们都会使用训练数据进行训练，并使用测试数据的评估结果来指导选择和更改各种模型超参数（如学习速率和特征）。这种方法有什么问题吗？

答案：多次重复执行此流程可能会导致我们不知不觉地拟合特定测试集的特性。
解释：我们根据给定测试集进行评估的频率越高，出现隐式过拟合该测试集的风险就越大。

1.2 验证集

将数据集划分为训练集和测试集。通过此分区，您可以基于一组样本进行训练，然后针对另一组样本测试模型。使用两个部分时，工作流程可能如下所示：
将数据集划分为两个集合固然不错，但不是万能的。 通过将数据集划分为下图所示的三个子集，您可以大大降低过拟合的可能性： 将单个数据集划分为三个子集。

使用验证集评估训练集的结果。 然后，在模型“通过”验证集之后，使用测试集仔细检查您的评估。

在这个经过改进的工作流程中：

1. 选择在验证集上获得最佳效果的模型。
2. 请对照测试集仔细检查该模型。

反复使用测试集和验证集会逐渐变耗。 也就是说，使用相同数据来做出有关超参数设置或其他模型改进的决策越多，您对这些结果实际泛化到未知新数据的信心就越低。 如果可能，最好收集更多数据来“刷新”测试集和验证集。重新开始是一个很好的重置机会。

2.特征工程

图 1 左侧表示来自输入数据源的原始数据，右侧表示特征向量，该矢量是构成数据集中样本的一组浮点值。 特征工程是指将原始数据转换为特征向量。进行特征工程预计需要大量时间。

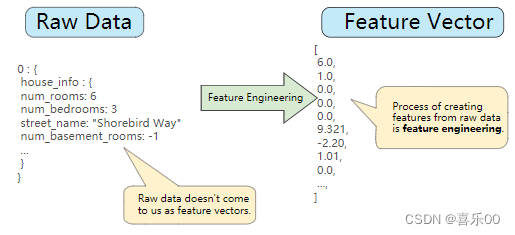
许多机器学习模型必须将特征表示为实数向量，因为特征值必须乘以模型权重。

2.1.1映射数值

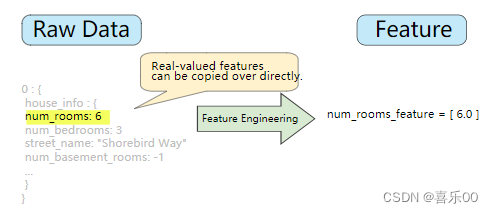
整数和浮点数据不需要特殊编码，因为它们可以与数字权重相乘。如图 2 所示，将原始整数值 6 转换为特征值 6.0 非常简单： 图 2. 将整数值映射到浮点值

2.1.2映射分类值

分类特征具有一组离散的可能值。例如，可能有一个名为 street_name 的功能，其中包含以下选项：

{'Charleston Road', 'North Shoreline Boulevard', 'Shorebird Way', 'Rengstorff Avenue'}

由于模型无法将字符串与学习到的权重相乘，因此我们使用特征工程将字符串转换为数值。
该向量的长度等于词汇表中的元素数。当单个值为 1 时，该表示法称为独热编码；当多个值为 1 时，这种表示法称为多热编码。

2.1.3 稀疏表示法

假设您的数据集中有 100 万个不同的街道名称，您想要将其添加为 street_name 的值。如果明确创建一个包含 100 万个元素的二元向量，其中只有 1 个或 2 个元素为 true，那么在处理这些向量时，就存储时间和计算时间而言，这种做法的效率非常低下。在这种情况下，一种常用的方法是使用 稀疏表示法，其中仅存储非零值。在稀疏表示法中，仍然会为每个特征值学习独立的模型权重，如上所述。

2.2良好特征的特点

1.避免很少使用的离散特征值
好的特征值在数据集中出现的次数应超过 5 次。这样一来，模型就可以学习此特征值与标签之间的关系。也就是说，有许多离散值相同的样本可让模型有机会在不同设置中看到相应特征，进而确定何时可以很好地预测标签。
相反，如果特征的值仅出现一次或极少出现，则模型无法根据该特征进行预测。

2.最好能提供清晰明确的含义
每个特征都应对项目中的任何人而言都有明确的含义。
例如，下面的良好特征有明确的名称，且值在名称方面有意义：

✔house_age_years: 27
相反，对于以下特征值的含义，除了创建它的工程师之外，其他人几乎都无法理解：
✘house_age: 851472000
在某些情况下，噪声数据（而不是糟糕的工程选择）会导致值不明确。例如，以下 user_age_years 的来源未检查值是否正确：
✘user_age_years: 277

3.请勿将“神奇”的值与实际数据混用
良好的浮点特征不包含超出范围的异常不连续或“神奇”值。

例如，假设一个特征具有一个介于 0 到 1 之间的浮点值。因此，如下所示的值没有问题：
✔quality_rating: 0.82 quality_rating: 0.37
但是，如果用户没有输入 quality_rating，则数据集可能使用如下特殊值表示不存在：
✘quality_rating: -1

如需明确标记魔法值，请创建一个布尔值特征来指示是否提供了 quality_rating。将此布尔特征命名为 is_quality_rating_defined。
在原始特征中，替换特殊值，如下所示：

• 对于采用一组有限值的变量（离散变量），请向集合中添加一个新值，并使用该值来表示特征值缺失。
• 对于连续变量，请使用特征数据的平均值，确保缺失值不会影响模型。
  4.考虑上游不稳定性
  特征的定义不应随时间而变化。

例如，以下值是有用的，因为城市名称一般不会更改。（请注意，我们仍需将“br/sao_paulo”这样的字符串转换为独热矢量。）
✔city_id: "br/sao_paulo"
但收集其他模型推断出的值会产生额外的费用。也许值“219”目前代表圣保罗，但在将来运行另一个模型时，这种表示法很容易改变：
✘inferred_city_cluster: "219"

2.3 清理数据

作为机器学习工程师，您将花费大量时间来抛弃不良样本并清理掉可以挽救的样本。即使只有少数“坏苹果”也会破坏大型数据集。

2.3.1 缩放特征值

缩放是指将浮点特征值从自然范围（例如 100 到 900）转换为标准范围（例如 0 到 1 或 -1 到 +1）。 如果某个特征集仅包含一个特征，则缩放几乎没有实际好处。但是，如果特征集由多个特征组成，则特征缩放可带来以下好处：

• 有助于梯度下降法更快地收敛。
• 帮助避免“NaN 陷阱”。在这种陷阱中，模型中的一个数值变成 NaN（例如，当某个值在训练期间超过浮点精确率限制时），并且模型中的所有其他数值最终也会因数学运算而变成 NaN。
• 帮助模型为每个特征学习适当的权重。 如果不进行特征缩放，模型会过于关注范围较大的特征。
  您不必对每个浮点特征执行完全相同的缩放。如果特征 A 的范围是 -1 到 +1，而特征 B 的范围是 -3 到 +3，则不会发生任何糟糕的情况。但是，如果特征 B 的范围是 5,000 到 100,000，则模型的响应会很糟糕。
  

2.3.2.处理极端离群值

下面的曲线图表示加利福尼亚州住房数据集中名为 roomsPerPerson 的地图项。roomsPerPerson 的值的计算方法是将某个区域的房间总数除以该区域的人口数量。该曲线图显示，加利福尼亚州的绝大部分地区每人一到两个房间。不过我们来看一下 x 轴。

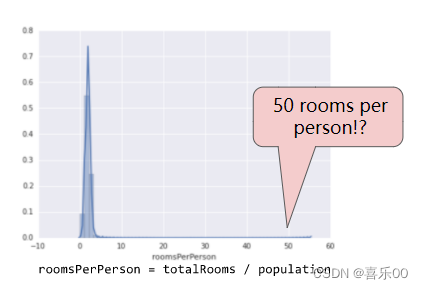
我们如何最大限度地降低这些极端离群值的影响？一种方法是对每个值取对数：

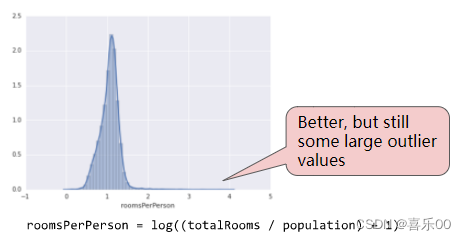
对数缩放的效果稍好一些，但仍有一个离群值显著尾巴。我们选择另一种方法。如果我们只是简单地将 roomsPerPerson 的最大值“限制”或“裁剪”为任意值（如 4.0），会发生什么情况？

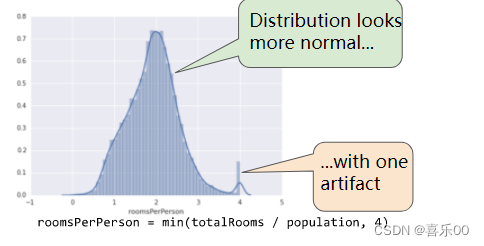
将特征值限制在 4.0 并不意味着我们会忽略所有大于 4.0 的值。而是意味着所有大于 4.0 的值现在都会变成 4.0。这解释了 4.0 处这个有趣的小山。 尽管存在这个小山，但缩放后的特征集现在比原始数据更有用。

3.分箱
下面的曲线图显示了加利福尼亚州不同纬度的房屋相对普及率。请注意聚类 - 洛杉矶大致位于纬度 34 度，旧金山大约在纬度 38 度。

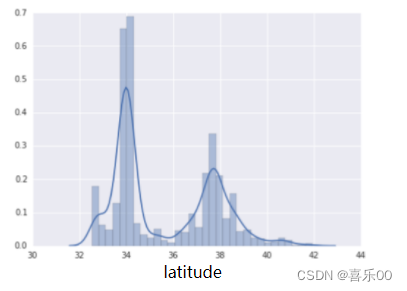
在数据集中，latitude 是一个浮点值。不过，在我们的模型中将 latitude 表示为浮点特征没有意义。这是因为纬度和房屋价值之间不存在线性关系。例如，纬度 35 处的房屋并不比
3534
纬度 34 处的房屋贵（或不贵）高。然而，单独的纬度很可能能够很好地预测房屋价值。
为了让纬度成为有用的预测指标，我们将纬度划分为“分箱”，如下图所示：

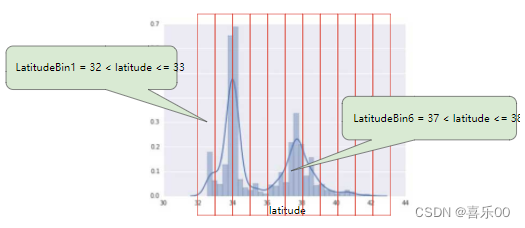
现在，我们拥有 11 个不同的布尔值特征（LatitudeBin1、LatitudeBin2、…、LatitudeBin11），而不是使用一个浮点特征。拥有 11 个单独的特征有点不方便，因此让我们将它们合并成一个包含 11 元素的向量。这样，我们就可以这样表示纬度 37.4，如下所示：

[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]

得益于分箱，我们的模型现在可以针对每个纬度学习完全不同的权重。

2.3.4.刷洗

到目前为止，我们假定用于训练和测试的所有数据都是可信的。在现实生活中，数据集中的许多样本都是不可靠的， 原因如下：

• 省略的值。例如，有人忘记输入某个房屋的年龄值。
• 重复样本。例如，服务器错误地将同一条记录上传了两次。
• 不良标签。例如，有人错误地将一棵橡树的图片标记为枫树。
• 特征值错误。例如，有人多输入了一个数字，或者温度计被遗落在太阳下。

一旦检测到不良样本，您通常可以通过从数据集中移除不良样本来“修正”这些样本。要检测遗漏值或重复样本，您可以编写一个简单的程序。检测不良特征值或标签可能要困难得多。
除了检测各个不良样本之外，您还必须检测集合中的不良数据。直方图是一种直观呈现汇总数据的绝佳机制。此外，获取如下统计信息也会有所帮助：

• 最大值和最小值
• 平均值和中位数
• 标准差

考虑生成离散特征的最常见值列表。 例如，country:uk 的样本数是否符合您的预期。language:jp 真的应该是您数据集中最常用的语言吗？