深入理解Java中的二叉树

news2024/10/5 17:35:06

目录

一、什么是二叉树?

二、二叉树的主要类型

三、二叉树的实现

四、二叉树的应用

五、关于二叉树的题目

引言:
二叉树是计算机科学中常用的一种数据结构，它是由节点组成的层级结构，每个节点最多有两个子节点。在Java编程语言中，二叉树常用于解决各种问题，如搜索、排序和树形结构组织等。本篇博客将深入讨论Java中二叉树的概念及其实现方式，并提供实例以帮助读者更好地理解。

一、什么是二叉树?

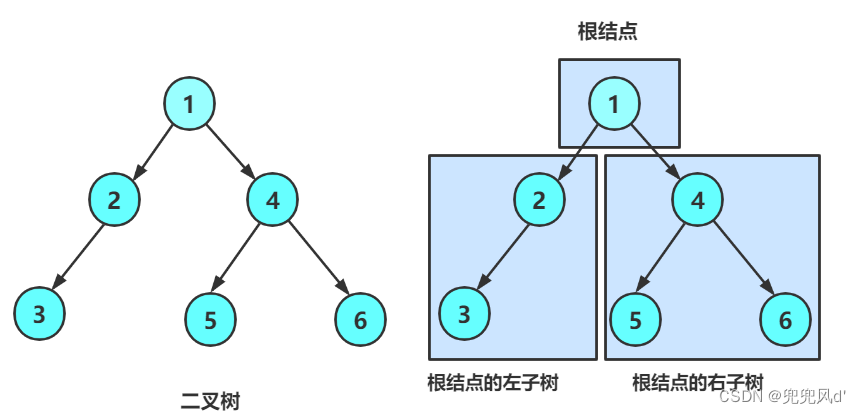
二叉树是由节点组成的树形结构，每个节点最多有两个子节点，分别称为左子节点和右子节点。它具有以下特性:

每个节点最多有两个子节点。
左子节点总是在父节点的左边，右子节点总是在父节点的右边。
二叉树的子树仍然是二叉树。

二、二叉树的主要类型

在Java中，二叉树主要有三种类型：二叉搜索树、满二叉树和完全二叉树。

二叉搜索树(Binary Search Tree, BST): 二叉搜索树是一种特殊的二叉树，它的每个节点的左子树的值都小于该节点的值，右子树的值都大于该节点的值。这使得二叉搜索树非常适合进行搜索和排序操作。
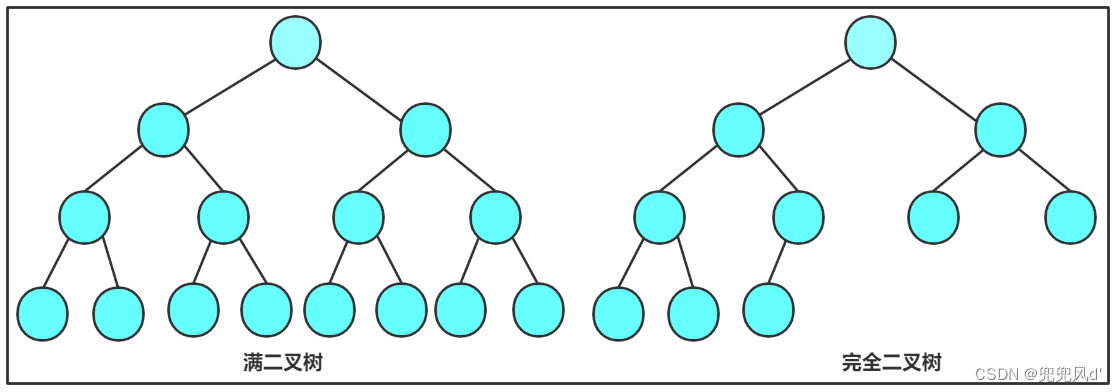
满二叉树(Full Binary Tree): 满二叉树是一种特殊的二叉树，除了叶子节点外，每个节点都有两个子节点。
完全二叉树(Complete Binary Tree): 完全二叉树是一种特殊的二叉树，除了最后一层的节点可能不满，其他层节点都被填充。

三、二叉树的实现

在Java中，可以使用节点类(Node class)和二叉树类(BinaryTree class)来实现二叉树。

节点类: 节点类表示二叉树中的一个节点，通常包含一个数据项和左、右子节点的引用。示例代码如下:

class Node {
    int data;
    Node left, right;
    
    public Node(int item) {
        data = item;
        left = right = null;
    }
}

二叉树类: 二叉树类包含节点的插入、搜索、删除等操作。示例代码如下:

class BinaryTree {
    Node root;
    
    // 构造函数
    BinaryTree() {
        root = null;
    }
    
    // 插入节点
    void insert(int data) {
        root = insertRecursive(root, data);
    }
     
    // 递归插入节点的辅助函数
    Node insertRecursive(Node root, int data) {
        if (root == null) {
            root = new Node(data);
            return root;
        }
     
        if (data < root.data)
            root.left = insertRecursive(root.left, data);
        else if (data > root.data)
            root.right = insertRecursive(root.right, data);
     
        return root;
    }
    
    // 搜索节点
    Node search(Node root, int data) {
        if (root == null || root.data == data)
            return root;
            
        if (data < root.data)
            return search(root.left, data);
     
        return search(root.right, data);
    }
    
    //... 还可以实现其他操作，如删除节点等
    
}

四、二叉树的应用

二叉树可以用于广泛的问题解决，以下是一些示例:

二叉搜索树常用于排序和搜索操作。
二叉树可以用于实现堆(heap)结构，如最大堆和最小堆。
表达式树(expression tree)可以用于解析和计算数学表达式。
二叉树可以用于建立文件系统或目录结构。
二叉树可以用于构建哈夫曼树(Huffman Tree)，用于数据压缩。
二叉树还可以用于实现图形界面的布局和组织等。

示例
下面是一个简单的示例，演示如何使用Java实现二叉树并执行一些基本操作：

public class BinarySearchTree {
    class Node {
        int data;
        Node left, right;
        
        public Node(int item) {
            data = item;
            left = right = null;
        }
    }

    Node root;

    BinarySearchTree() {
        root = null;
    }

    void insert(int key) {
        root = insertRecursive(root, key);
    }

    Node insertRecursive(Node root, int key) {
        if (root == null) {
            root = new Node(key);
            return root;
        }

        if (key < root.data)
            root.left = insertRecursive(root.left, key);
        else if (key > root.data)
            root.right = insertRecursive(root.right, key);

        return root;
    }

    void inorderTraversal(Node root) {
        if (root != null) {
            inorderTraversal(root.left);
            System.out.print(root.data + " ");
            inorderTraversal(root.right);
        }
    }

    public static void main(String[] args) {
        BinarySearchTree tree = new BinarySearchTree();

        tree.insert(50);
        tree.insert(30);
        tree.insert(20);
        tree.insert(40);
        tree.insert(70);
        tree.insert(60);
        tree.insert(80);

        System.out.println("Inorder traversal of the binary tree:");
        tree.inorderTraversal(tree.root);
    }
}

以上示例创建了一个二叉搜索树，并按中序遍历方式打印出树中的节点值。结果输出如下：