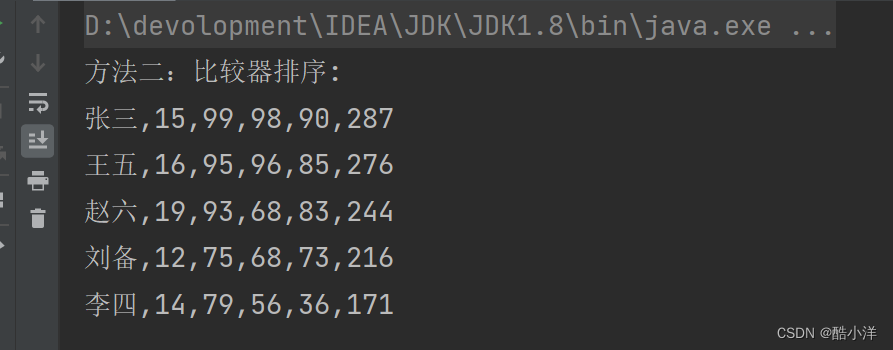
DP（动态规划）全称Dynamic Programming，是运筹学的一个分支，是一种将复杂问题分解成很多重叠的子问题、并通过子问题的解得到整个问题的解的算法。

在动态规划中有一些概念：
n<=1e3 [][] ，n<=100 [][][]
状态：就是形如dp[i][j］= val的取值，其中i，j为下标，也是用于描述、确定状态所需的变量，val为状态值。
状态转移：状态与状态之间的转移关系，一般可以表示为一个数学表达式，转移方向决定了迭代或递归方向。
最终状态：也就是题目所求的状态，最后的答案

1.确定状态，一般为“到第i个为止，xx为j（xx为k）的方案数/最小代价/最大价值”可以根据数据范围和复杂度来推理。
2.确定状态转移方程，即从已知状态得到新状态的方法，并确保按照这个方向一定可以正确地得到最终状态。
根据状态转移的方向来决定使用选代法还是递归法记忆化。
3.确定最终状态并输出。

数字三角形

蓝桥杯数字三角形


思路：可以用 dp也可以用动态规划，计算最大和，再判断向下和向右操作不大于 1。

• 动态规划
  O(n^3)

#include<bits/stdc++.h>
using namespace std;
const int N = 1e2 +5;
int n,a[N][N],dp[N][N][N];

int main(){
    memset(dp,-0x3f,sizeof(dp));
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>a[i][j];
    dp[1][1][0] = a[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++){
            for(int k=0;k<=n-1;k++){
                if(!k)dp[i][j][k] = dp[i-1][j-1][k] + a[i][j];
                else dp[i][j][k] = max(dp[i-1][j-1][k],dp[i-1][j][k-1]) + a[i][j];
            }
        }
    int ans=0;
    if((n-1)&1) for(int j=1;j<=n;j++) ans = max(ans,max(dp[n][j][(n-1)/2+1],dp[n][j][(n-1)/2]));
    else for(int j=1;j<=n;j++) ans = max(ans,dp[n][j][(n-1)/2]);
    cout<<ans<<'\n';
    return 0;
}

思路：由于最后的位置是有规律的，所以直接用[][]就行。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e2 +5;
int n,a[N][N],dp[N][N];

int main(){
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>a[i][j];
    dp[1][1] = a[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++)
            dp[i][j] = max(dp[i-1][j-1],dp[i-1][j]) + a[i][j];
    
    if((n-1)&1)cout<<max(dp[n][(n-1)/2+1],dp[n][(n-1)/2+1+1]);
    else cout<<dp[n][(n-1)/2+1];
    return 0;
}

思路：用 DFS,代码结果不对，不知道为什么

#include<bits/stdc++.h>
using namespace std;
const int N = 1e2+10;
int a[N][N],res[N][N],n;

int dfs(int i,int j){
    if(res[i][j])return res[i][j];
    if(i==n){
        if(n%2==0&&(j==(n-1)/2+1||j==(n-1)/2+1+1))return a[i][j];
        if(n%2==1&&j==(n-1)/2+1)return a[i][j];
        return -10000000;
    }
    return res[i][j] = max(dfs(i+1,j),dfs(i+1,j+1))+a[i][j];
}

int main( ){
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>res[i][j];
    cout<<dfs(1,1)<<'\n';
    return 0;
}