"Success is not final, failure is not fatal: It is the courage to continue that counts."
- Winston Churchill

1. 题目描述

2. 题目分析与解析
2.1 思路一——双指针
按照双指针的解法应该大家都能比较快的想出来,就是一个指针pointS指向字符串s,一个指针pointT指向字符串t,通过从前向后遍历t字符串,判断pointT指向的当前字符和pointS的字符是否相等,相等就将pointS指针也后移,如果pointS能够遍历结束则说明满足条件,返回true。
2.2 思路二——通过一个二维数组存放t字符串中每个字符及其对应下标
由于题目的进阶版本要求:
如果有大量输入的S,称作S1,S2,….,Sk其中k>=10亿,你需要依次检查它们是否为T的子序列。在这种情况下,你会怎样改变代码?
如果每个s都需要去遍历一遍t字符串,那么时间开销是很大的,所以我们现在就要想办法把 t 中的信息怎么存储起来来换取时间。之所以是需要存储 t 中的信息,是因为我们每一个 s 字符串是不相同的,而每一次的 t 字符串都是相同的,也就是说对于一个多次使用的东西,我们要想办法把他的信息最不能得高效的去利用。
因为我们想要达到的目的是遍历每一个s字符串,要在t中找到是否存在该序列,我们就可以通过遍历s的每一个字符,看t中是否有满足的匹配字符——不仅字符要匹配,而且下标要呈递增的模式。
-
因此我们就可以把 t 字符串中每一个字符的下标存储起来,这样我们就能够得到一个类似于二维数组的结构,如下:

-
而后对于每一个s字符串,遍历,根据当前字符找到对应的键,在下标数组中找到一个合适的下标,能找到就继续,不能找到就返回false。
-
这个合适的下标指的是:当前选择的下标要比上一次选择的下标大,保证字符间顺序。
-
同时这个寻找合适下标的过程,是可以运用二分查找的,这是因为我的下标数组肯定都是有序的,因为我是从前到后遍历t字符串,这样形成的下标数组肯定是升序的,给使用二分查找创造了条件。
算法执行主要步骤:
-
通过遍历长字符串t,把每一个字符出现的位置记录下来
-
然后遍历短字符串s,查找对应的字符在键值和下标数组的hashMap中是否存在,如果存在找到满足下标大于前一个字符在长字符串中下标的字符
-
该查找过程可以使用二分查找
-
也可以通过一个新的数组记录上一次在该字符处使用的位置
-
主要讲一下通过一个新的数组记录上一次在该字符处使用的位置的方法,见下图:
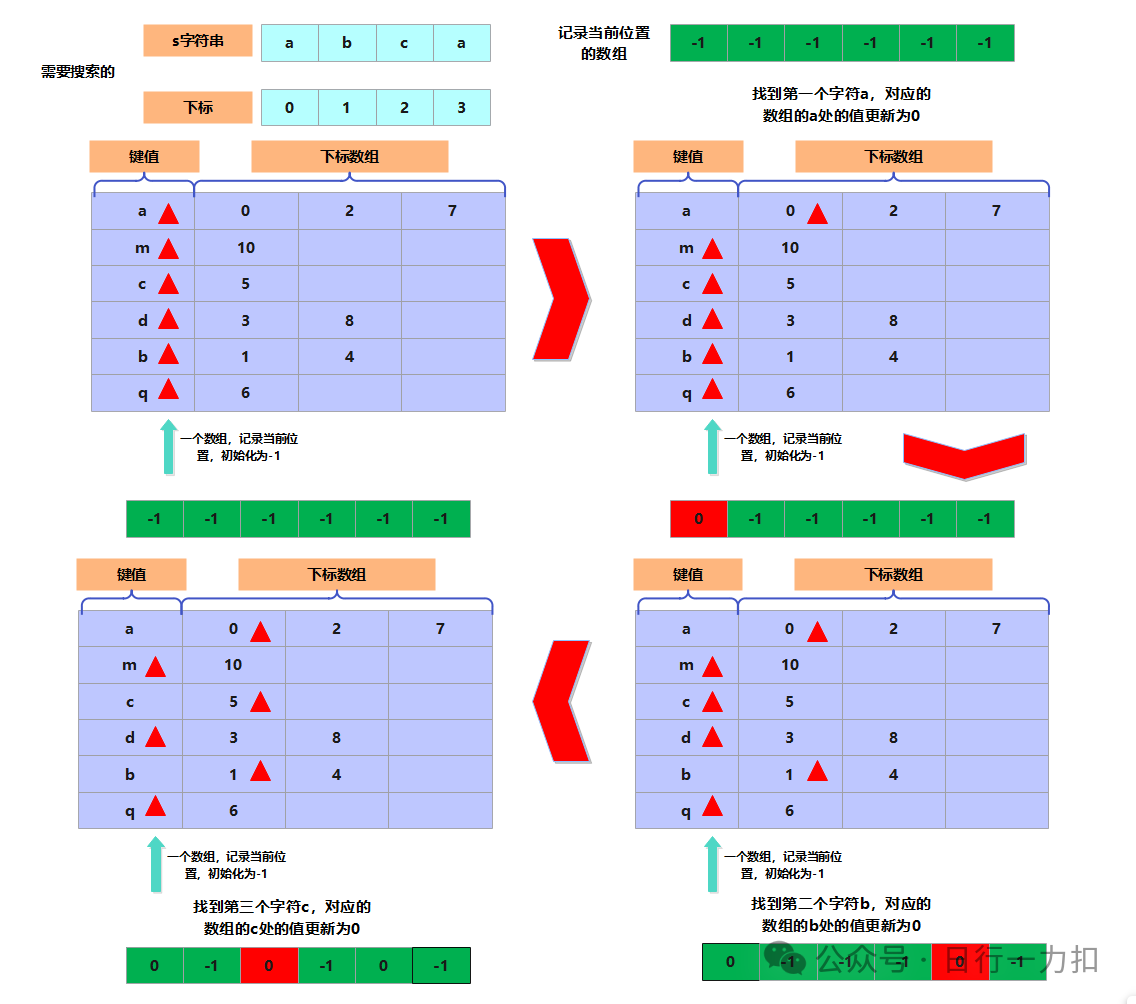
上图展示了找目标字符串s的前三个字符的过程,当找最后一个字符a时,因为我当前a对应的数组的值为0,所以下一次我就只需要从1处找是否有下标满足大于前一个下标也就是c的下标5的目标,如下:

3. 代码实现
3.1 思路一——双指针
// 判断子序列
public boolean isSubsequence(String s, String t) {
// 解题思路
// 1. 双指针判断是否为子序列,一个指向s,一个指向t,
// 如果s的指针指向的字符等于t的指针指向的字符,s的指针向后移动
// 最后判断s的指针是否指向了s的末尾
// 2. 时间复杂度O(n)
// 3. 空间复杂度O(1)
// 4. 代码实现
int i = 0, j = 0;
if (s.length == 0){
return true;
}
while (i < s.length() && j < t.length()) {
if (s.charAt(i) == t.charAt(j)) {
i++;
}
j++;
if (i == s.length()) {
return true;
}
}
return false;
}3.2 思路二——二维数组
3.2.1 使用二分查找
class Solution {
public boolean isSubsequence(String s, String t) {
int n = s.length(), m = t.length();
// 通过遍历长字符串,把每一个字符的位置记录下来
HashMap<Character, ArrayList<Integer>> hashMap = new HashMap<>();
for (int i = 0; i < m; i++) {
char ch = t.charAt(i);
if (!hashMap.containsKey(ch)) {
hashMap.put(ch, new ArrayList<>());
}
hashMap.get(ch).add(i);
}
// 用来记录上一个字符的索引
int preIndex = -1;
for (int i = 0; i < n; i++) {
// 方法1:使用二分查找在hashMap.get(s.charAt(i))找到大于preIndex得最小值
if (!hashMap.containsKey(s.charAt(i))) {
return false;
}
int left = 0;
int right = hashMap.get(s.charAt(i)).size() - 1;
// 二分查找过程
while (left < right) {
int mid = left + (right - left) / 2;
if (hashMap.get(s.charAt(i)).get(mid) <= preIndex) {
left = mid + 1;
} else {
right = mid;
}
}
if (hashMap.get(s.charAt(i)).get(left) <= preIndex) {
return false;
}
preIndex = hashMap.get(s.charAt(i)).get(left);
}
return true;
}
}3.2.2 使用数组记录下标
public boolean isSubsequence3(String s, String t) {
int n = s.length(), m = t.length();
// 通过遍历长字符串,把每一个字符的位置记录下来
HashMap<Character, ArrayList<Integer>> hashMap = new HashMap<>();
HashMap<Character, Integer> indexMap = new HashMap<>();
for (int i = 0; i < m; i++) {
char ch = t.charAt(i);
if (!hashMap.containsKey(ch)) {
hashMap.put(ch, new ArrayList<>());
}
hashMap.get(ch).add(i);
}
// 给indexArray初始化
for (Character c : hashMap.keySet()) {
indexMap.put(c, -1);
}
// 用来记录上一个字符的索引
int preIndex = -1;
// 然后遍历短字符串,看其相应的顺序,对应在hashMap对应得Array中最小的索引,最后看是否能找全
for (int i = 0; i < n; i++) {
// 没有该字母 || (该字母的索引已经到末位&&该字母的索引不是-1也就是不是第一个字母)
if ((!hashMap.containsKey(s.charAt(i)) || (hashMap.get(s.charAt(i)).get(hashMap.get(s.charAt(i)).size() - 1) <= indexMap.get(s.charAt(i))) && indexMap.get(s.charAt(i)) != -1)) {
return false;
}
// 理论上的下一个目标位置
int index = indexMap.get(s.charAt(i)) + 1;
// 有对应的下标
if (index < hashMap.get(s.charAt(i)).size()) {
// 找到大于preIndex得最小值
while (preIndex >= hashMap.get(s.charAt(i)).get(index)) {
index++;
if (index == hashMap.get(s.charAt(i)).size()) {
break;
}
}
//没找到
if (index == hashMap.get(s.charAt(i)).size()) {
return false;
}
//找到了
indexMap.put(s.charAt(i), index);
preIndex = hashMap.get(s.charAt(i)).get(index);
}
//无对应的字母键
else {
return false;
}
}
return true;
}4. 运行结果
4.1 双指针
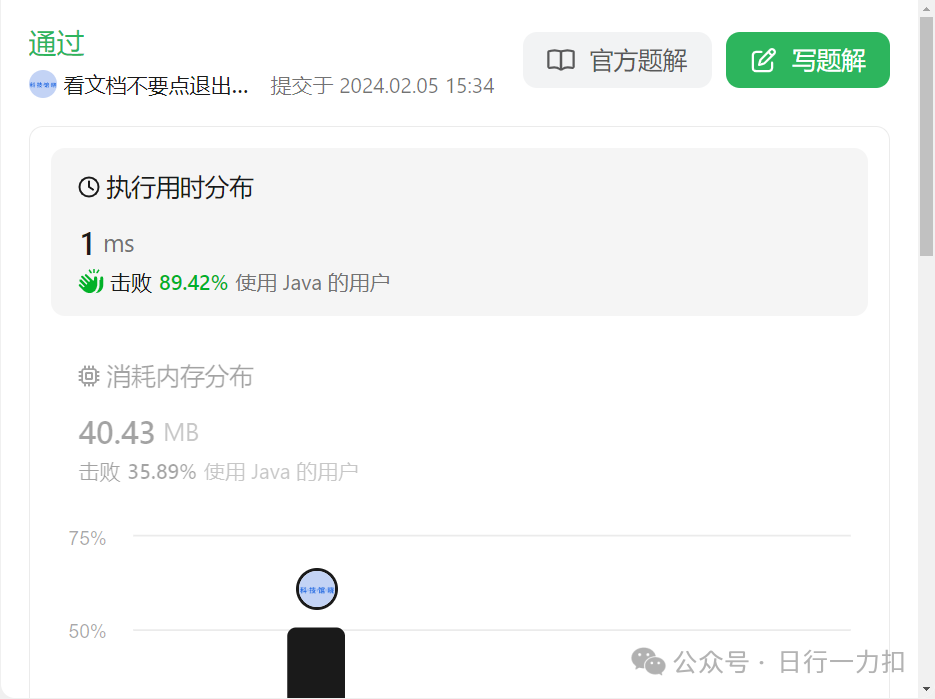
4.2 二维数组——二分和数组记录下表相同
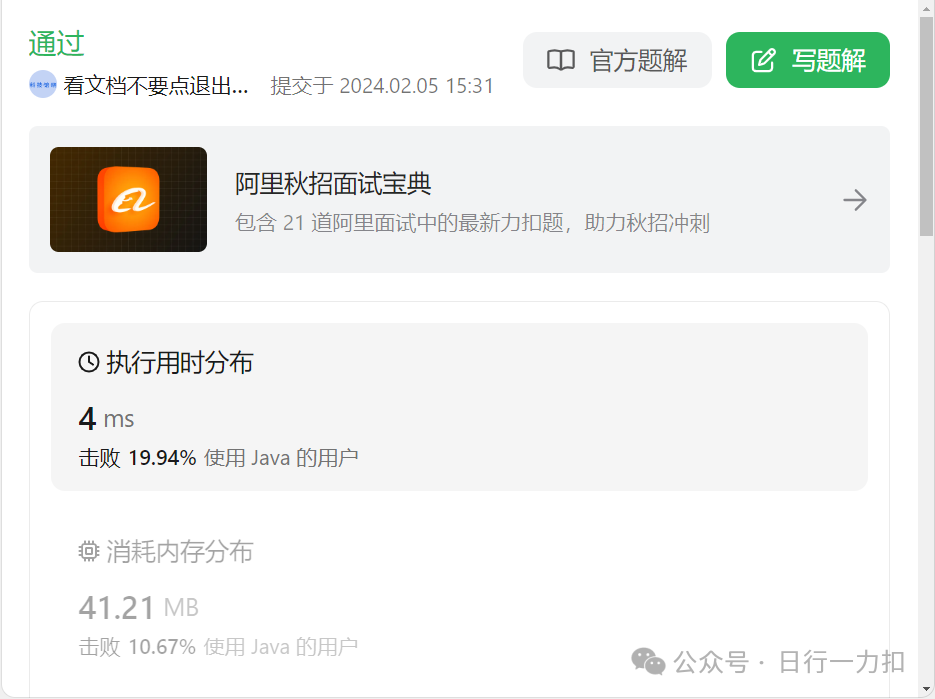
5. 相关复杂度分析
5.1 双指针
-
时间复杂度:O(n+m),n为字符串t的长度,m为字符串s的长度。循环同时对s和t进行,每次无论是匹配成功还是失败,都有至少一个指针发生右移,两指针能够位移的总距离为n+m。
-
空间复杂度:0(1),声明了2个变量
5.2 二维数组(二分查找)
-
时间复杂度:O(MlogN+N),N为字符串s的长度,M为字符串t长度。对t中的每个字符都需要logN的查找一次;而且为了处理出待查找的序列,还需要O(N)的遍历字符串S。
-
空间复杂度:O(N),需要一个大小为N的哈希表。
本人公众号,专注简单易懂的算法解析
下一篇:使用动态规划解决该题目