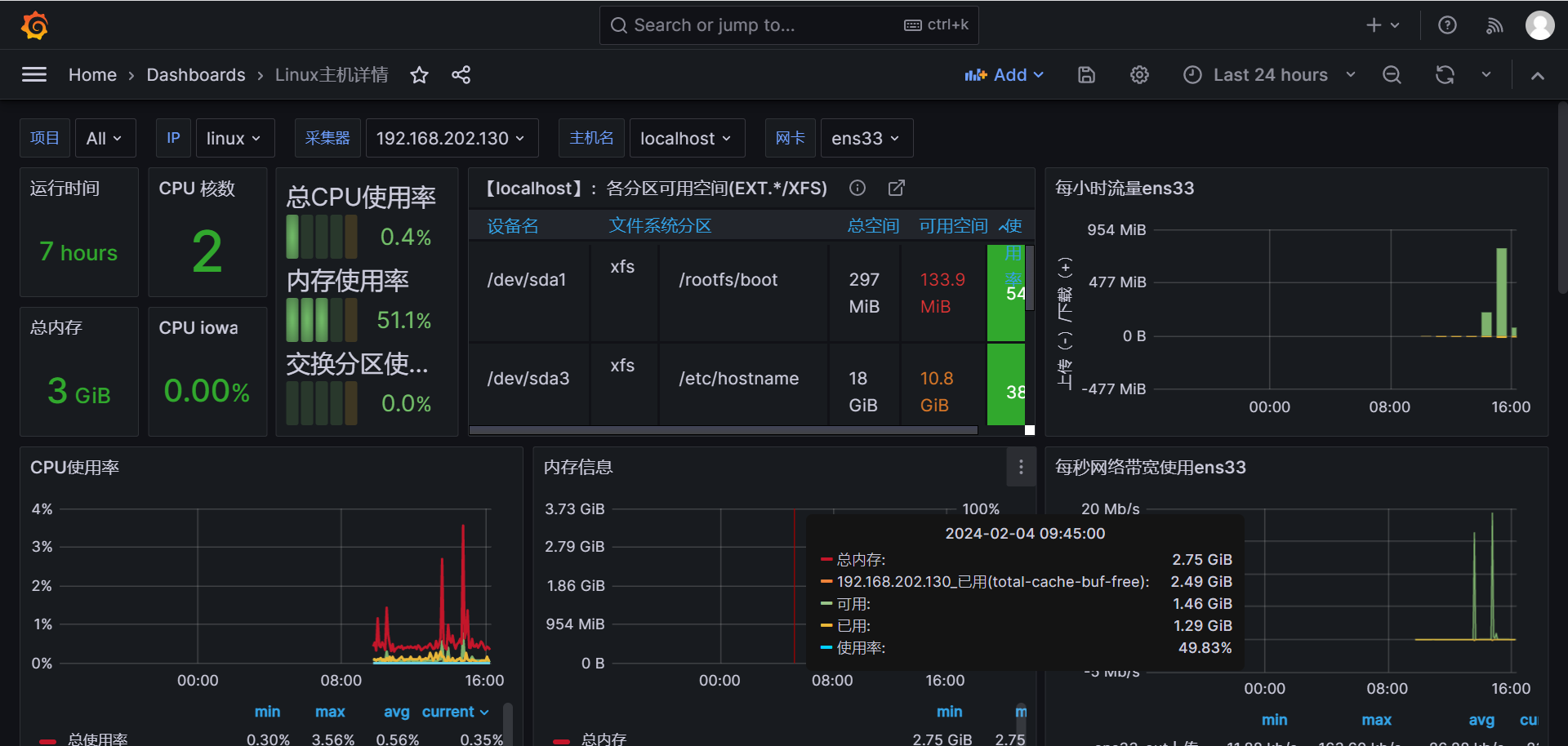
错排公式理解:


//f(x)表示1~x的错排数目
//
//1选择(x-1种)
//乘以剩下的总数目就是答案。
//(1选了2就接着排2了,这样所有的都可以算到,是递归所以难想)
// 选2时
// 2可选 1 和 3~x
//2选1,对2开始来说此次总数就是1*f(x-2)
//2选3~x时,我们可以把'不选位'1移到2下,也就是2不选1,(就相当于2不选2啦)这个等价f(x-1),
//即接下来的情况数就是2~x(即1~x-1)错排数目
// 上面两种情况相加 是 2之后的所有选法
// *1的所有选法即是答案
//
//f[x] = (x-1)*(f[x-1]+f[x-2])
//f[1] = 0
//f[2] = 1
代码:
const ll mod = 1e9 + 7;
ll a[1000005];
ll f[1000005];
ll ksm(int x, int y, int mod) {
if (x == 1) return 1;
ll res = 1, base = x;
while (y) {
if (y & 1) res = (res * base) % mod;
base = (base * base) % mod;
y >>= 1;
}
return res;
}
ll C(ll n, ll m, ll p)
{
if (m > n)return 0;
return ((a[n] * ksm(a[m], p - 2, p)) % p * ksm(a[n - m], p - 2, p) % p);
}
ll A(ll n, ll m, ll p)
{
if (m > n)return 0;
return (a[n] * ksm(a[n - m], p - 2, p)) % p;
}
void solve(int casen)
{
int n, m;
cin >> n >> m;
if (n == m)
cout << C(n, m, mod) % mod << endl;
else
cout << C(n, m, mod) * f[n - m] % mod << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t = 1;
cin >> t;
a[0] = 1;
for (int i = 1; i <= 1000000; i++)
{
a[i] = i * a[i - 1] % mod;
}
f[1] = 0, f[2] = 1;
for (int i = 3; i <= 1000000; i++)
{
f[i] = (i - 1) * (f[i - 1] + f[i - 2])%mod;
}
for (int i = 1; i <= t; i++)
{
solve(i);
}
return 0;
}