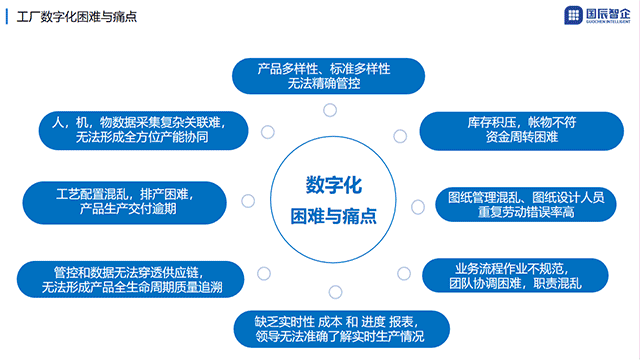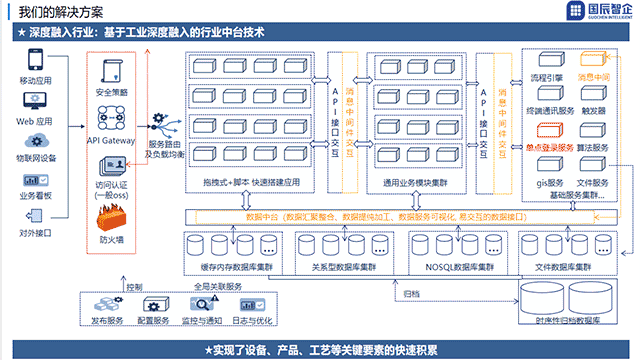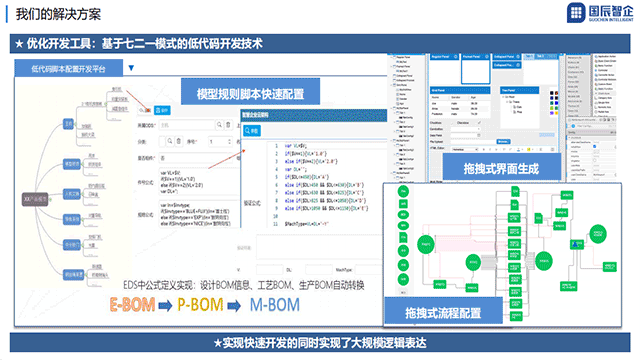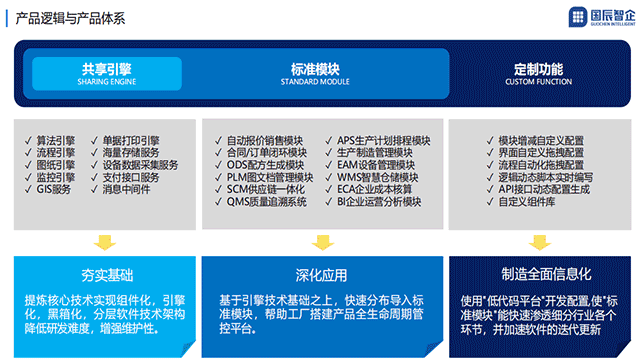
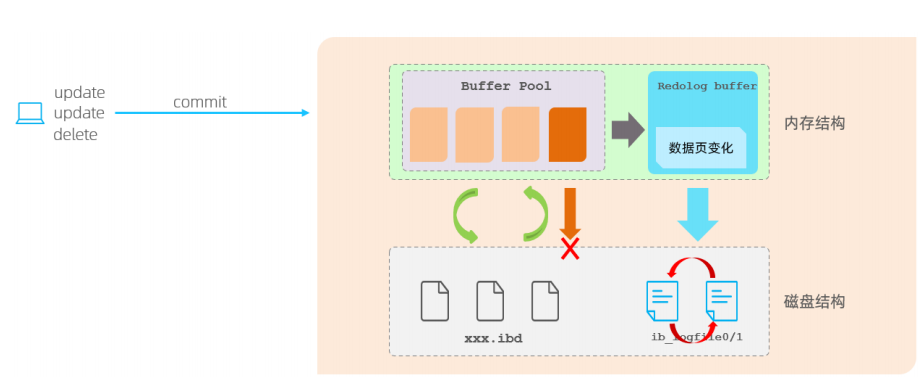
343. 整数拆分 

代码随想录

视频讲解：动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili

class Solution {
    public int integerBreak(int n) {
    // 1.确定dp数组（dp table）以及下标的含义：对i进行拆分，得到的最大的乘积为dp[i]
    // 2。确定递推公式：两个数i * (i - j), 三个数 j * dp[i - j] (不拆j因为dp[i-j]包含这种情况)
    // 3.dp数组如何初始化：dp[0],dp[1]初始成0，dp[2]=1
    // 4.确定遍历顺序：从3开始遍历
    // 5.举例推导dp数组：
        int dp[] = new int[n + 1];
        dp[0] = 0;
        dp[1] = 0;
        dp[2] = 1;
        for (int i = 3; i < n + 1; i++) {
            for (int j = 1; j < i; j++) {
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

 96.不同的二叉搜索树 

代码随想录

视屏讲解：动态规划找到子状态之间的关系很重要！| LeetCode：96.不同的二叉搜索树_哔哩哔哩_bilibili

class Solution {
    public int numTrees(int n) {
    // 1.确定dp数组（dp table）以及下标的含义：1到i为节点组成的二叉搜索树的个数为dp[i]。
    // 2。确定递推公式：dp[i] += dp[j - 1] * dp[i - j]; 
    //     j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
    // 3.dp数组如何初始化：dp[0] = 1
    // 4.确定遍历顺序：
    // 5.举例推导dp数组：
        int dp[] = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}