张维迎《博弈与社会》威胁与承诺（3）承诺行为

承诺的作用

上一节，我们探讨了如何在求解博弈时把不可置信的威胁或许诺排除出去，从而对参与人的行为做出合理的预测。如前所述，其中一个隐含的前提条件是，参与人要具有理性共识。而理性共识是一个要求很高的条件，现实生活中往往难以做到。这也使得不可置信的威胁或许诺经常出现在我们的生活中。

尽管如此，这一理论对现实仍然有很强的解释能力。比如，金融危机的发生很大程度上是惩罚的不可信导致的。如果经营不善的企业必须倒闭，欠债不还的人必须坐牢，每个人融资时就都会谨慎行事，就不会过度负债，金融危机就可能避免——至少不会那么严重。但现实中，由于担心大企业，特别是大的金融机构的倒闭会带来一系列的社会问题，一旦大企业出现债务危机，政府就会出手救助。这种现象被称为“大而不倒”（too big to fail）。预期到这一点，企业在融资时就更喜欢冒险，因为成功的收益归己，失败的成本可以由社会承担，结果出现了金融危机。

再比如，在传统的农村社会，男女结婚要依循媒妁之言、父母之命，但总会有年轻人自由恋爱，老父亲知道后可能就会要求女儿与男友分手，否则就威胁断绝父女关系。老父亲的这个威胁是不可信的，因为如果真的与女儿断绝关系，老父亲的损失更大。如果女儿知道老父亲是理性的，她就不会顺从。所以，经常发生的情形是，女儿和男友私奔了，等过几年抱着小孩回来后，老父亲也就会认了这门亲事。

由于存在着不可置信的威胁或许诺，使得人和人之间一些有效率的合作无法实现，即无法实现帕累托最优。

以前述图所示的博弈为例。按照前文的分析，我们知道这一博弈的结果为参与人1选择U之后，博弈结束，参与人1和2分别得到2和0。但这个纳什均衡不是帕累托最优的。现在，假如参与人1向参与人2许诺，如果我先选择D，只要你答应选择R，我接下来就再选择D′。如果参与人2相信参与人1的许诺，自己选择R，而参与人1也信守诺言选择了D′，这时，参与人1得到4，参与人2得到2。这一结果相对于原来的博弈结局使得两个人的收益都提高了，可以称为帕累托改进。

首先注意到，参与人2有积极性答应参与人1自己会选择R，即使他并没有积极性实际上这样做。但问题是，参与人2选择R之后，参与人1会背弃诺言，选择U′，让自己得到收益5，参与人2这时的收益就只有0了。参与人2会预料到这种情况，因而不会选择R，而会选择L，确保自己的收益为1。这样一来，参与人1知道参与人2的应允会落空，一开始就不会选择D，而会选择U，确保自己得到2。也就是说，每个人都有积极性许诺，但谁都没有积极性兑现自己的许诺，因为都不相信对方的许诺，从而帕累托改进无法实现。

政府与市场的关系也是类似。如果政府不能让市场相信它不会轻易改变政策，市场就会出现短期化行为。比如我国目前的房地产市场种种混乱的局面主要就是政府政策摇摆所致。政府曾高调宣布“调整经济结构”不仅事关全局，还迫在眉睫，为调整经济结构开始对房地产进行打压。但是市场怀疑一旦经济增长放慢速度，政府还是要把保增长放在更加突出的位置，从而就会放松对房地产市场的控制，于是房价还要反弹。因此，政府调控房地产的政策要想有效，关键是如何让自己的威胁或许诺变得可信。

在这种情况下，如何使许诺或威胁变得可信，就成为帕累托最优能否通过纳什均衡实现的关键。在前述例子中，如果参与人1能够采取某种行动，让自己选择D′的许诺变得可信，那么参与人2就会选择R，双方的合作就可以实现了。比如，参与人1在博弈开始前，拿出价值为2的保证金交给一个独立的第三方，宣称如果到博弈的第三阶段，他不选择D′的话，第三方就可以把他的保证金没收。这样一来，到了博弈的第三阶段，如果参与人1选择U′的话，其收益就只剩下3了，不如选择D′得到收益4。因此，此时参与人1向参与人2许诺如果参与人2选择R，自己将选择D′就变得可信了。

前文已经提到，不可置信威胁的根源在于事先最优与事后最优的不一致。比如，师生博弈中学生“不及格就报复”的威胁，事先看是最优的，但事后看并不是。父女博弈中，“断绝父女关系”的威胁事前看是最优的，但一旦女儿私奔后，事后就不是最优的。债务博弈中，事前看惩罚是最优的，但事后看救助是最优的。政府与市场博弈中，事前看“调结构”是最优的，事后看可能需要“保增长”。

在博弈论中，如果某个参与人采取某种行动，使得一个原来事后不可置信的威胁变成一个事后可以置信的威胁，事前最优和事后最优相一致，则这种行动被称为承诺（commitment）。注意，这里“承诺”和前面提到的“许诺”（promise）的含义有所不同。“许诺”和“威胁”都可以看成是一种言辞上的表示；而“承诺”指的是一种行动，言而有信。语言是矮子，行动是巨人。这表明承诺比许诺重要，只有通过承诺，才能使得原本不能实现的帕累托最优成为均衡结果。

承诺的成本

让承诺能够发挥作用的关键是承诺需要花费成本。在上例中，参与人1所交的价值为2的保证金实际上就是参与人1的承诺成本。显然，承诺的成本越高，就会使得许诺的可信性越大，从而合作实现的可能性就越大。上例中，如果参与人1交的保证金低于1的话，该许诺仍然是不可信的。现实中的一个例子是，淘宝网曾于2011年10月10日宣布建立“商家违约责任保证金”制度，向淘宝商城内的商家收取1万元至15万元不等的“信用保证金”。尽管此事曾经在淘宝网和入驻的商家之间掀起一阵风波，但应该承认的是，提高保证金的确会起到让商户更加守信的作用。

在我国古代的婚姻关系中，由于结婚后男方可以通过“一纸休书”就把婚离了，因此尽管结婚之前男方山盟海誓，但女方仍担心嫁过去后，男方会不遵守诺言，始乱终弃。这种情况下，男方可以通过送昂贵“彩礼”，或举办成本极高的婚礼，来对自己的婚姻行为做出承诺：如果男方结婚后写休书的话，彩礼就不退了。显然，男方送的彩礼越贵重，婚礼的成本越高，其承诺作用就越强。一次婚姻就几乎倾家荡产的人是不大可能离婚的。

在创业投资中，创业者出资的数量也能起到承诺作用。创业者出资越多，投资者可能越愿意投资。因为一旦创业者不好好经营的话，他的损失是很大的。更一般地，一个人对其财产拥有的所有权可以起到他对社会的承诺作用。也就是说，“恒产者有恒心”。比如中产阶级参与革命的可能性比较小，而没有资产的人群，因为机会成本小，更有可能揭竿而起。有一定资产的人希望社会是稳定的，因为如果社会不稳定，动荡不安，他们的损失也会更大。从这个意义上讲，中产阶级是社会稳定的重要因素。

承诺行动的实质是限制自己的选择范围，即放弃某些选择，或使得如果不选择所许诺行为而是选择其他行为的话，就要付出更高的代价。选择少，让自己的许诺变得可信，反倒对自己有利。这实际上是“置之死地而后生”的道理。比如，我们都知道项羽“破釜沉舟、背水一战”的故事。公元前207年，项羽的军队和秦军主力部队在巨鹿作战，项羽只有20万人，而秦军有30万人，在这种情况下，“项羽乃悉引兵渡河，皆沉船，破釜甑，烧庐舍，持三日粮，以示士卒必死，无一还心。”这样一来，项羽的士兵都明白，别无选择，要想活命，只有拼命一搏了。最后，项羽的士兵九战九捷，打败了秦朝的主力军队。

批注：commitment，interesting。

通过限制己方的选择可以让己方的许诺或威胁变得可信。同样，增加对方的选择也可以让对方的许诺和威胁变得不可信。这可以称为“反承诺”策略。比如《孙子兵法》第七篇“军争篇”中提到“围师必阙，穷寇勿迫”的说法，前者是说如果己方包围敌军时，并不是要四面围住，而要围住三面放一面，这样敌军就会从未被包围的城门逃跑，己方就可以较为轻松地占领城池。但如果所有城门都被围，守军无路可逃，只有一个选择，那就是抗争到底，造成己方增添伤亡。后者是说，对于没有战斗能力、陷于绝境的敌人不要过于追迫他，否则有可能让其狗急跳墙、鱼死网破。这两句话的共同含义都是指通过给敌人提供更多的选择而消磨对方的抵抗意志，让对方无法进行血战到底的承诺。

承诺是企业在市场竞争中经常使用的策略。1991年诺贝尔经济学奖获得者罗纳德·科斯在1972年发表的《耐用消费品和垄断》一文中就认识到，生产耐用品的垄断企业需要对消费者进行承诺，因为即使没有对手，它也经常面临现在和未来之间的竞争（Coase, 1972）。举例而言，假设某企业的生产成本为0，他可以生产1单位耐用消费品，也可以生产2、3或4个单位产品。如果生产1单位，消费者愿意支付的最高价是100，这样，企业利润也是100；如果生产2单位，消费者愿意支付的最高价是80，企业的利润为160；如果生产3单位，消费者愿意支付的最高价是50，利润为150；如果生产4单位，消费者愿意支付的最高价是30，企业得到的利润是120。如果从利润最大化的角度，企业应该生产2单位产品，获利160。但是进一步思考会发现，最好的办法是先生产第一个单位，并卖给愿意出100的消费者；然后再生产第二个单位，并卖给出价80的人；再继续生产第三个单位，卖给出价50的人；最后生产第四个单位，卖给出价30的消费者。这样就总共可以赚到260，这可以说是最大的利润了。

不过问题在于，第一个消费者会预计到自己买后企业就会降价，因此他会选择等待。同理，第二个人也会等待，因为他预期产品的价格会继续下降到50，第三个人预期价格会下降到30，同样会选择等待。所以最后产品的价格为30，这就是著名的科斯猜想。

这样的困境显然对企业不利。为了改变困境，企业可能会告诉第一个消费者，自己只会生产一个单位的产品，但如果消费者是理性的，他显然不会相信。为此，厂商需要做一个承诺，比如补差价。企业可以最初定价80，并起草一个销售条款，规定如果一年之内降价的话，厂商就会把差价返还给已经购买了产品的人。如果这个条款具有法律上的可执行性，或者企业非常重视自己的声誉，就不会降价了，因为，多生产一个单位的产品卖出50，但必须给原来的两个买主返还60，得不偿失。通过这个承诺，科斯猜想中的困境就会得到解决了。

画家和前述的生产耐用消费品的厂商性质类似。画是耐用消费品，而且时间越长可能越值钱。如果一个著名画家准备出售一幅名画，由于重新画一幅画的成本很小，画家同样面临科斯猜想中的困境。画家要想把画卖一个好价钱，必须要承诺自己不会画太多的画。如何让市场相信画家不会画太多的话，对于画家来说是非常困难的。口说无用。极端的情况是，画家过世等于是一个不会再画的承诺。所以，我们经常看到一个画家在死后其作品更加值钱的现象。同样的道理，邮政局发行纪念邮票时，为让其升值，往往会把印刷邮票的原版毁掉，起到的也是承诺作用。

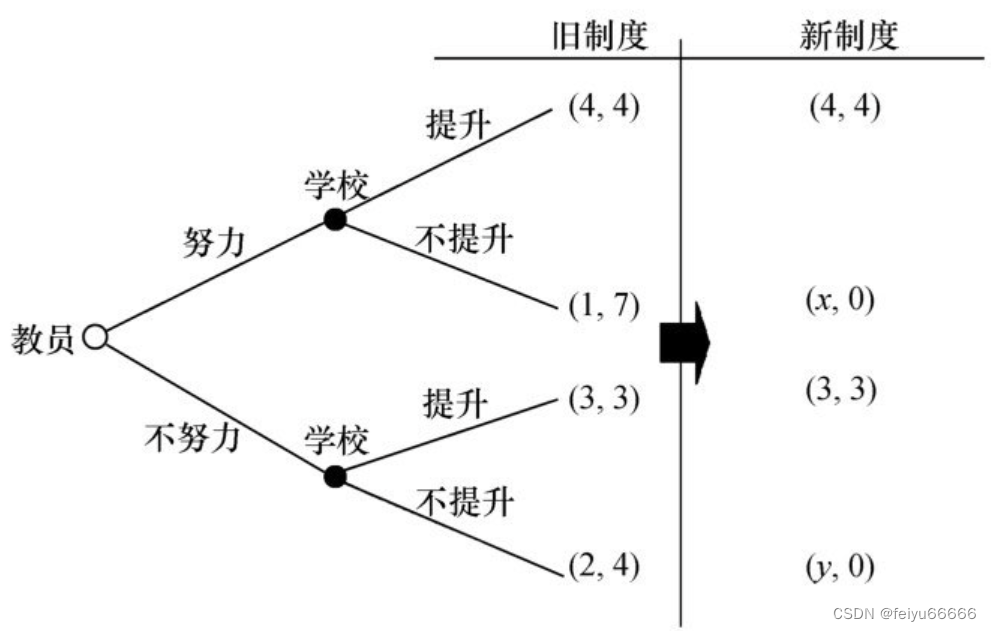
我们也可以用这个理论来解释大学改革。北大改革很重要的一个方面是实行“不升即走”（up or out）的制度，也就是说，讲师和副教授阶段的老师，都有可能被淘汰。“不升即走”其实可以理解为大学不压制人才的承诺。如果没有这样的承诺，优秀的人才可能会被埋没、被压制，教授就得不到公平的待遇。这一机制可以用图所示的博弈来说明。

在这个博弈中，教员可以选择努力或者不努力，学校可以选择提拔或者不提拔。假定教员努力，可以创造总价值8。在旧制度下，如果学校提拔教员，教员和学校各得到4；但如果学校不提拔，教员得到1，学校得到7。如果教员不努力，学校同样需要决定是否提升。如果提升的话，教员和学校各得到3，加起来是6；如果不提升，学校得到4，教员得到2。博弈的均衡是教员不努力、学校不提升（或者说，提升不提升与努力无关）。

“不升即走”可以改变这个博弈的均衡。在新制度下，如果教员努力而得到提升，双方的收益都为4；但如果教员努力而得不到提升，他会选择离开，这样学校得到0，教员走出去以后得到的收益假定是x（具体依赖于他自身的能力与市场价值）。如果教员不努力，而学校提升他，双方的收益都为3。如果教员不努力，而学校不提升他，教员离开，他的收益为y，学校的收益为0。新制度下博弈的均衡是什么？如果教员努力，学校提升他，学校得到4，不提升学校得到0，所以学校会选择提升。如果教员不努力，即使被学校提升，他也只能得到3，少于在努力情况下被学校提升时得到的4，所以教员的最优选择是努力。最后的均衡结果是教员努力，学校提升。

读者可能会有疑问：旧制度下，如果学校对教员不公正，教员还可以继续待下去，而新制度下，如果学校对教员不公正，教员就必须走人，这不是更不公正吗？新制度的优越性恰恰来自这里。在旧制度下，一个教员无论多么优秀，因为他不能离开，学校不提升他仍然可以利用他，可谓“价廉物美”，学校也就没有压力保持公正。在新制度下，如果学校对教员不公正，优秀教员也有更高的市场价码，优秀人才流失以后，真正损失的是学校，学校就不敢对教员不公正。也就是说，正因为“不升即走”，学校就必须公正。所以说，“不升即走”是学校的一个承诺：不会亏待优秀人才。