D. A Simple Task

题意

给定一个简单图（无重边无自环），求出其中的环的数量（一个环除了起点和终点一样以外，没有另外的两个相同的点）

思路

为了区分不同的环，我们可以统一地用环内编号最小来区分，我们假设每个环都是从编号最小出发，然后回到这个编号最小的点。定义：$dp[S][u]$ 为当前访问的点集合为 $S$，且最后一个访问的点是 $u$ 的路径数量，起点的话就是 $S$ 中最低位的那个 $1$，也就是环内编号最小的那个点 $bit$。我们每次扩展 $u$ 的邻居 $v$ 时，只考虑编号大于等于 $bit$ 的点，这样子我们就维护了环内编号最小的起点终点的唯一性，避免了重复计数。

当 $v=bit$ 时，$ans+=dp[S][u]$，因为这时候已经可以通过 $u\to v=bit$ 这条路回到这个编号最小的点了，环的数量就是 $bit\to u$ 的路径数量。

我们初始化 $\forall i\in [0,n),dp[1<<i][i]=1$，分别表示以这些点为环内最小编号的那些有效路径，在递推的过程中，一个状态的最小编号总是不变的。

最后对于那些直连边，我们会错误统计上去，所以最终答案要减去初始边的数量。

并且每个环会被统计两遍，所以答案还要除 $2$。例如以 $3$ 为环内编号最小的点：

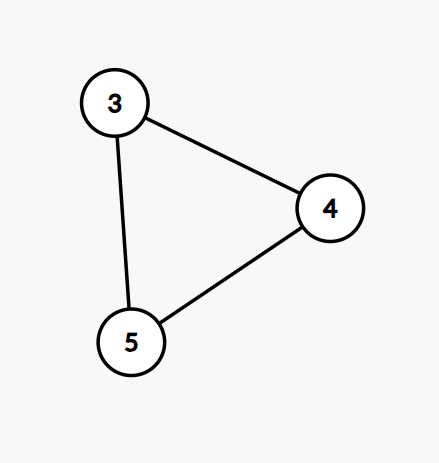
这个环会被算两遍：

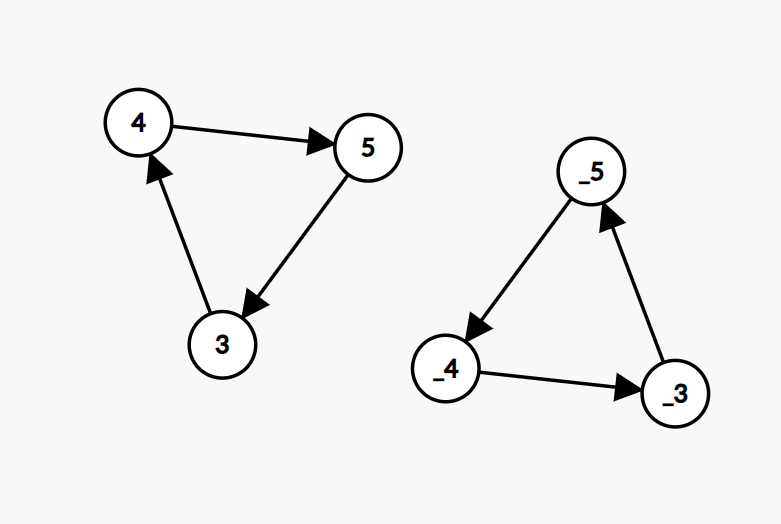
#include<bits/stdc++.h>
#define fore(i,l,r)	for(int i=(int)(l);i<(int)(r);++i)
#define fi first
#define se second
#define endl '\n'
#define ull unsigned long long
#define ALL(v) v.begin(), v.end()
#define Debug(x, ed) std::cerr << #x << " = " << x << ed;
#define lowbit(x) ((x) & -(x))

const int INF=0x3f3f3f3f;
const long long INFLL=1e18;

typedef long long ll;

const int N = 20;

ll dp[1 << N][N];
std::vector<int> g[N];

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int n, m;
    std::cin >> n >> m; 
    fore(i, 0, m){
        int u, v;
        std::cin >> u >> v;
        --u;
        --v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    fore(i, 0, n) dp[1 << i][i] = 1;
    ll ans = 0;
    fore(S, 1, 1 << n){
        fore(u, 0, n){
            if(!dp[S][u]) continue;
            int bit = std::__lg(lowbit(S)); //访问的点中编号最小的
            for(auto v : g[u]){
                if(v < bit) continue; //维持环内编号最小不变
                if(!(S >> v & 1))
                    dp[S | 1 << v][v] += dp[S][u]; 
                else if(v == bit)
                    ans += dp[S][u];
            }
        }
    }
    ans -= m; //减去直连边
    ans >>= 1; //每一条环会算两遍
    std::cout << ans;
    return 0;
}