1 基础示例
1.1 例题一
有如下程序,设计分别满足语句覆盖和分支覆盖的最有效力的测试用例。
int x = 0;
int y = 0;
if (x > 0 && y > 0)
{
y = y/x;
}
if (x > 1 || y > 1)
{
y = y + 1;
}
x = x + y;
分析:
语句覆盖只需要所有的语句都被执行过即可,针对此程序,只需要使两个if语句都为true即可,例如x=2,y=0。
分支覆盖,也叫判定覆盖,只需要所有的判断都能取到所有可能的值即可,针对此程序,只需要使两个if语句各自都取到true和false即可,例如x=2,y=0(两个if都是true); x=0,y=0(两个if都是false)需要两条用例。
1.2 例题二
有如下程序,变量i取什么值能效力最高的满足判断覆盖?
void main()
{
int i = 0;
int sum = 0;
scanf("%d", &i);
while(i <= 10)
{
sum += i;
i++;
}
printf("%d\n", sum);
}
分析:
此程序中,while语句是路径分支。效力最高的满足判断覆盖,即在最小的循环执行次数下,判断可以取到true和false。因此,取i=10,满足true,下一轮循环i变为了11,满足false。
1.3 例题三
有如下程序,满足判定覆盖至少需要几条测试用例?
int func(int n)
{
if (n == 0)
{
return33;
}
if (n == 1)
{
return66;
}
if (n > 1)
{
return func(n - 1) + func(n - 2) + func(n - 3) ;
}
else
{
return99;
}
}
分析:
此程序中,2个if和1个if-else组成了所有的判断,满足判定覆盖,即需要让所有的判定各取true和false。最简单直观的是用4条用例n=0; n=1; n=2; n=-1即可满足,注意到程序里有递归调用,实际上取n=2,会调用return func(1) + func(0) + func(-1) ;即可满足。
2 进阶示例
有如下程序,设计各种逻辑覆盖的测试用例:
int test (int x, int y)
{
int ret = 0;
if (x > 0 && y > 0)
{
ret = x + y + 10; //语句块1
}
else
{
ret = x + y - 10; //语句块2
}
if (ret < 0)
{
ret = 0; //语句块3
}
return ret; //语句块4
}
分析:根据程序,先画出流程图:
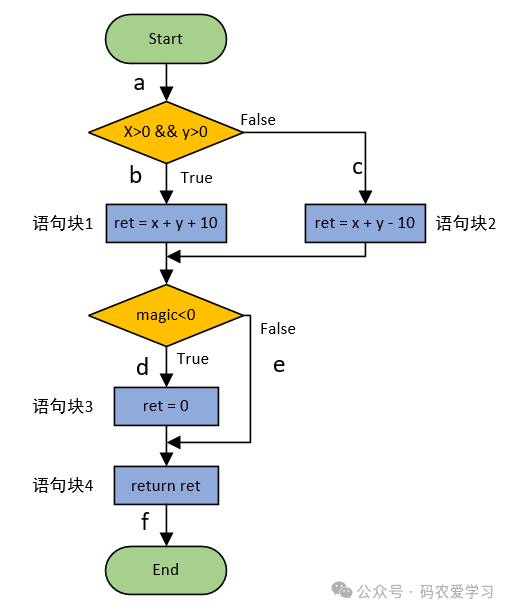
2.1 语句覆盖SC
设计满足语句覆盖(SC)的测试用例,即运行完测试用例,能将程序中每条可执行语句至少被执行一次。
本例中,就是要把语句块1~语句块4都执行一遍。
| 用例数据 | 语句块1 | 语句块2 | 语句块3 | 语句块4 |
|---|---|---|---|---|
| {x=3, y=3} | √ | - | abef | √ |
| {x=-3, y=0} | False | √ | √ | √ |
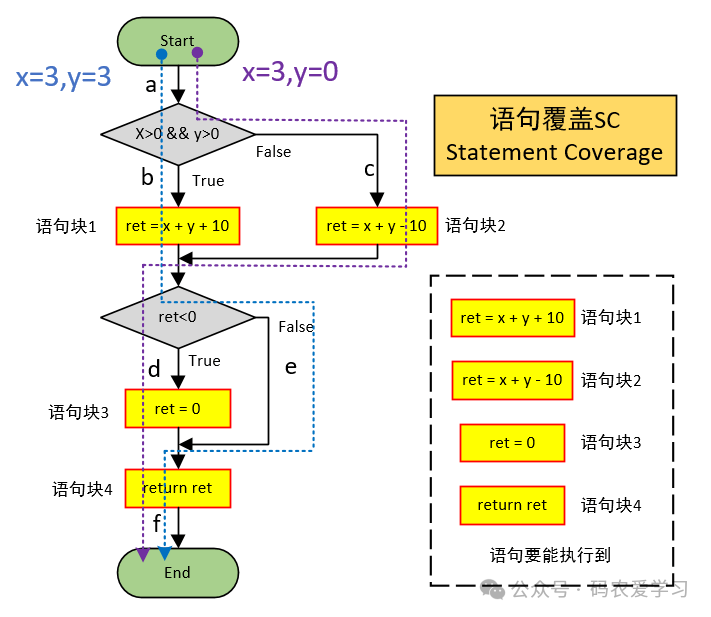
2.2 判定覆盖DC
设计满足判定覆盖(DC)的测试用例,即运行完测试用例,使得程序中每个判断的True和False分支至少被执行一次。
判定覆盖,也叫分支覆盖
| 用例数据 | P1(x>0&&y>0) | P2(ret<0) |
|---|---|---|
| {x=3, y=3} | True | False |
| {x=-3, y=0} | False | True |
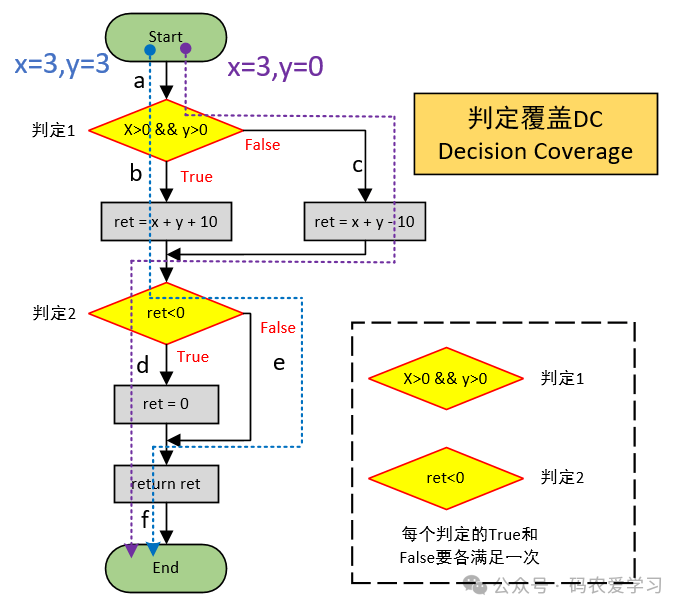
2.3 条件覆盖CC
设计满足条件覆盖(CC)的测试用例,即运行完测试用例,使得程序中每个逻辑条件的可能值至少被满足一次。
| 用例数据 | C1(x>0) | C2(y>0) | C3(ret<0) | P1(x>0&&y>0) | P2(ret<0) |
|---|---|---|---|---|---|
| {x=3, y=0} | True | False | True | False | True |
| {x=-3, y=15} | False | True | False | False | False |
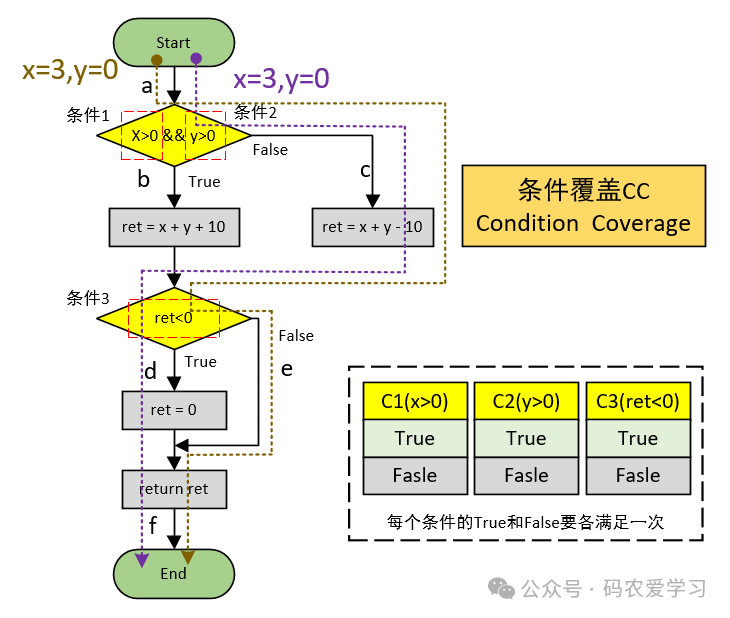
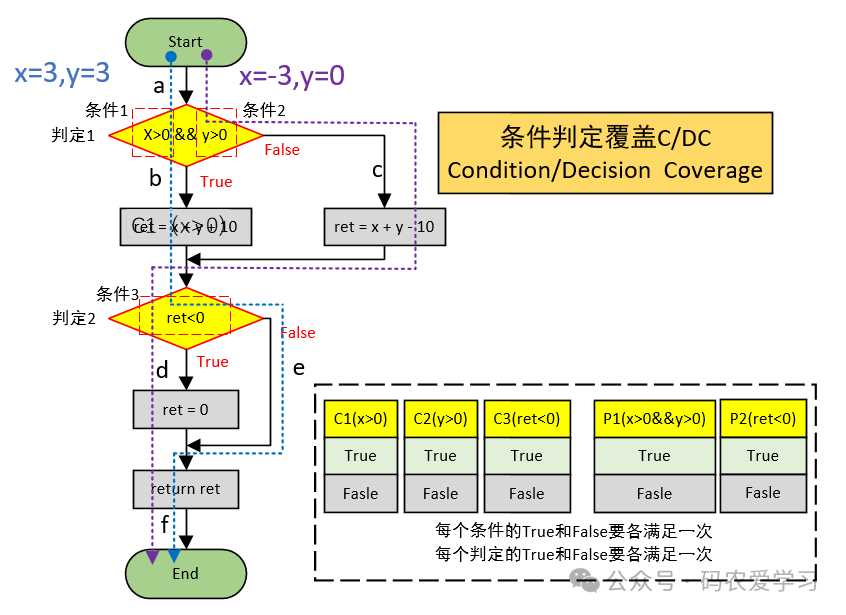
2.4 条件判定覆盖C/DC
设计满足条件判定覆盖(C/DC)的测试用例,即运行完测试用例,使得程序中每个判断的True和False分支至少被执行一次,同时,使得程序中每个逻辑条件的可能值至少被满足一次。
| 用例数据 | C1(x>0) | C2(y>0) | C3(ret<0) | P1(x>0&&y>0) | P2(ret<0) |
|---|---|---|---|---|---|
| {x=3, y=3} | True | True | False | True | False |
| {x=-3, y=0} | False | False | True | False | True |
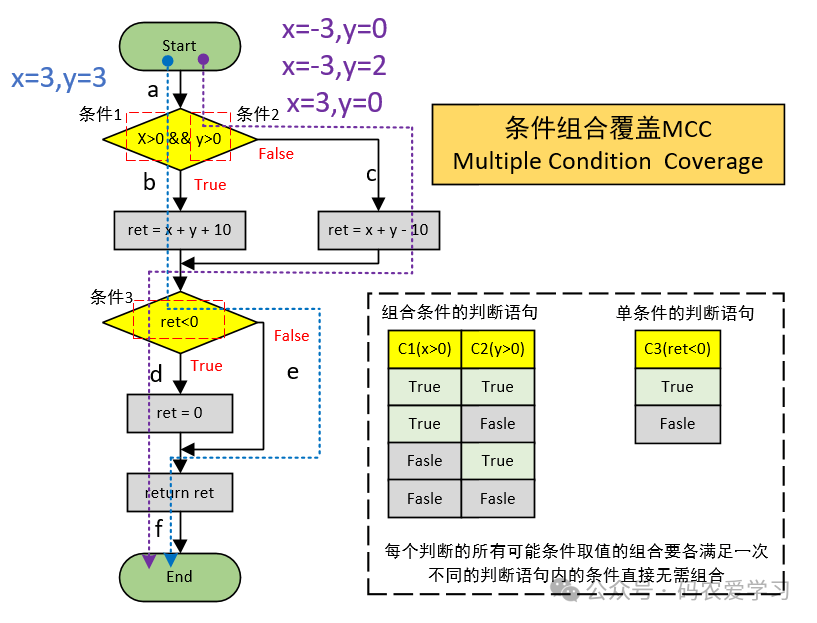
2.5 条件组合覆盖MCC
设计满足组合覆盖(MCC)的测试用例,即运行完测试用例,使得程序中每个判断的所有可能条件取值的组合至少被满足一次。
注意几点:
-
条件组合只针对同一个判断语句内存在多个条件的情况
-
不同的判断语句内的条件直接无需组合
-
对于单条件的判断语句,只需满足自己的所有取值即可
| 用例数据 | C1(x>0) | C2(y>0) | C3(ret<0) | P1(x>0&&y>0) | P2(ret<0) | 路径 |
|---|---|---|---|---|---|---|
| {x=-3, y=0} | False | False | True | False | True | acdf |
| {x=-3, y=2} | False | True | True | False | True | acdf |
| {x=3, y=0} | True | False | True | False | True | acdf |
| {x=3, y=3} | True | True | False | True | False | abef |
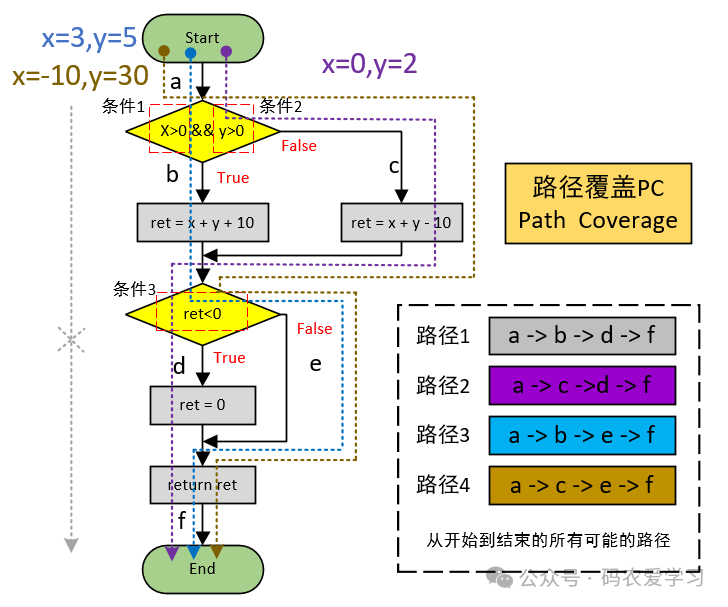
2.6 路径覆盖PC
设计满足路径覆盖(PC)的测试用例,即运行完测试用例,使得程序中每条路径至少被覆盖一次。
| 用例数据 | C1(x>0) | C2(y>0) | C3(ret<0) | P1(x>0&&y>0) | P2(ret<0) | 路径 |
|---|---|---|---|---|---|---|
| 不可能路径 | - | - | - | - | - | abdf |
| {x=0, y=2} | False | True | True | False | True | acdf |
| {x=3, y=5} | True | True | True | True | True | abef |
| {x=-10, y=30} | False | True | False | False | False | acef |
3 修正的条件判定覆盖MC/DC
修正的条件判定覆盖MC/DC,这里再描述一下含义:
MC/DC要求设计适当数量的测试用例,满足以下条件:
保证在一个程序中每一种输入输出至少出现一次
在程序中的每一个条件必须产生所有可能的输出结果至少一次
并且每个判断中的每个条件必须能独立影响一个判断的输出(即在其它条件不变的前提下,仅改变这个条件的值,而使判断结果改变)
有如下程序,若要满足修正的条件判定覆盖,最少的测试用例需要几条:
bool func(bool x, bool y, bool z)
{
if (x && (y || z))
{
returntrue;
}
returnfalse;
}
先画出流程图,这里给出两种画法:
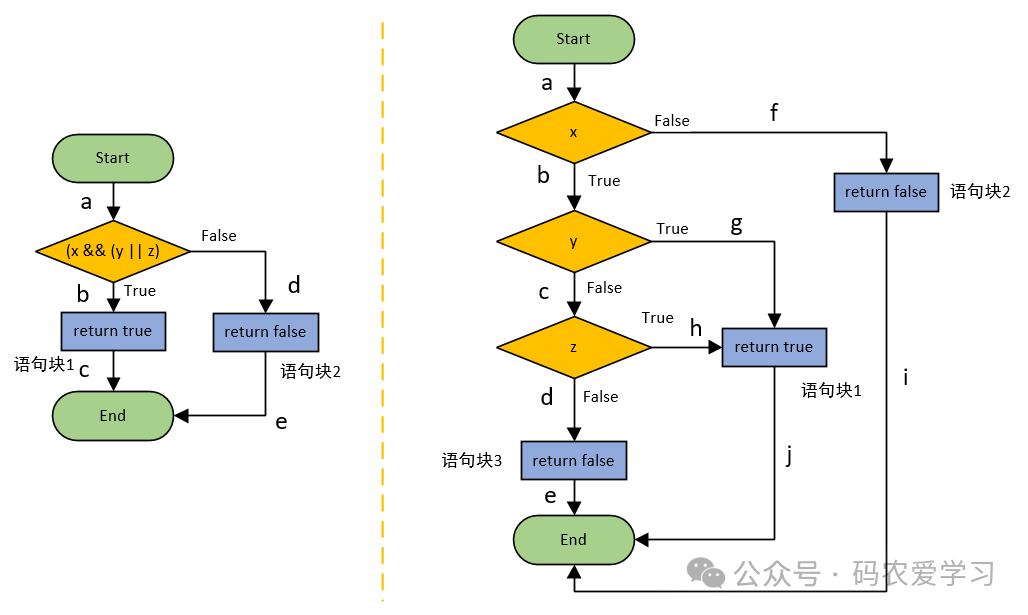
对于修正的条件判定覆盖:
-
首先需要先进行条件组合,本例中P1判定内包含3个布尔值的条件x、y、z,对其组合有8种情况
-
然后再分别对每个条件的用例进行计算,规则为:
-
条件Cx所在的判定内(本例即P1),除条件Cx外,其它条件的取值完全相同(例如对于C1,就是找到与x的值相反,y和z相同的用例 )
-
判定的结果与之相反(例如对于C1,用例2和用例6的判定结果就是相反的)
-
按照以上规则,可以得到如下表:
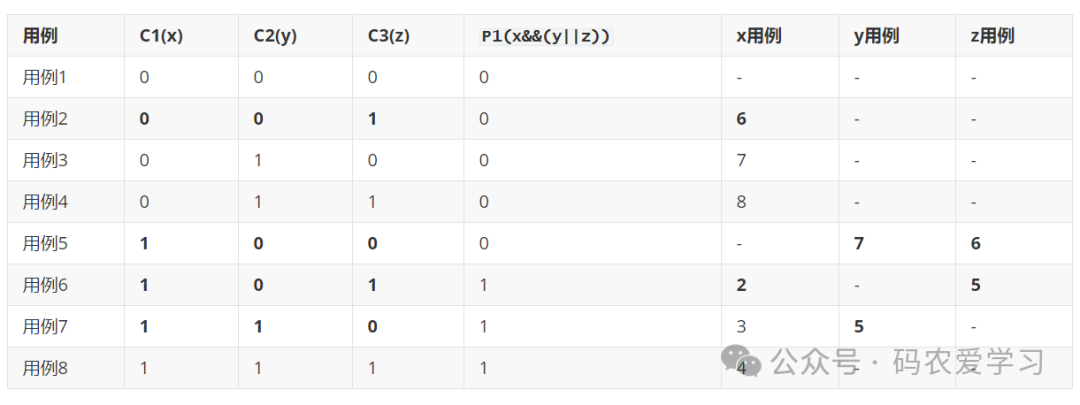
观察表格:
-
对于条件z,需要选用用例5和6
-
对于条件y,需要选用用例5和7
-
对于条件x,需要选用用例2和6,或用例3和7,或用例2和8
为了实现最少的用例能满足MC/DC,可选的用例组合为:
-
组合1:用例2、用例5、用例6、用例7
-
组合2:用例3、用例5、用例6、用例7
即最少需要4条用例才能满足MC/DC。
例如选择组合1,将冗余的用例去除,得到如下表:
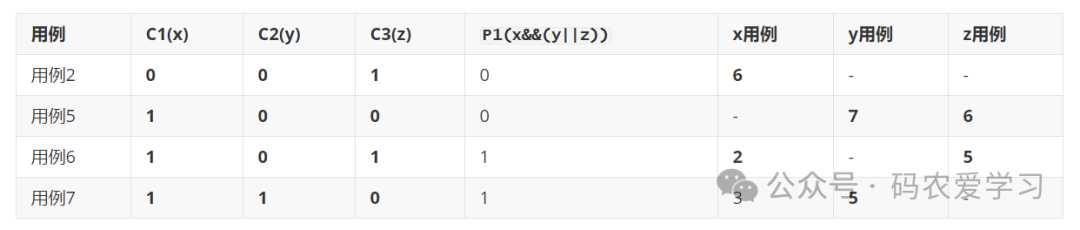
再来分析一次:
-
对于条件x,使用用例2和6来测试,y和z的值相同(y=0,z=1),P1判定结果刚好是不同值(0和1)
-
对于条件y,使用用例5和7来测试,x和z的值相同(x=1,z=0),P1判定结果刚好是不同值(0和1)
-
对于条件z,使用用例5和6来测试,x和y的值相同(x=1,y=0),P1判定结果刚好是不同值(0和1)
最后,再来通过在流程图上标注来对比看下,加深理解:
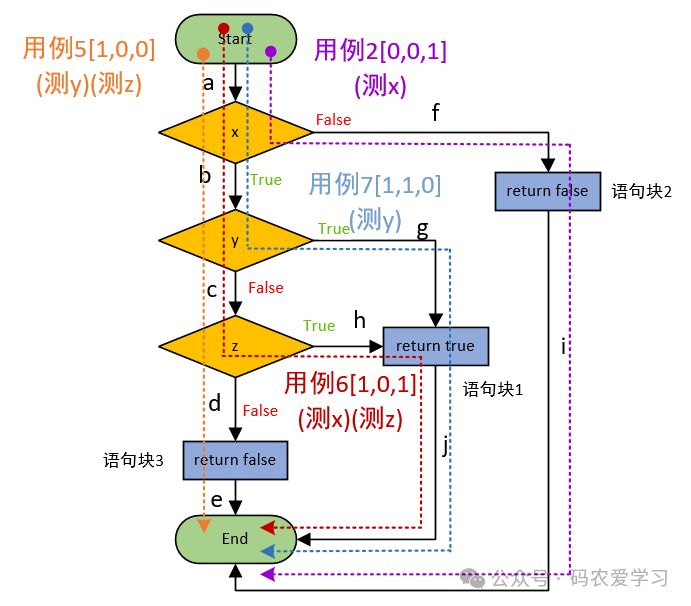
4 总结
本篇介绍了软件测试中,白盒测试中逻辑覆盖的各种实例情况,包括语句覆盖SC、判定覆盖DC、条件覆盖CC、条件判定覆盖C/DC、条件组合覆盖MCC、路径覆盖PC、修正的条件判定覆盖MC/DC的实例。